Gawroński Wojciech
III rok chemii inf.
WYZNACZANIE STAŁEJ SZYBKOŚCI I RZĘDU REAKCJI
Celem ćwiczenia jest określenie przy pomocy metody fotometryczynej rzędu reakcji oraz wyznaczenie stałej szybkości reakcji i czasu połowicznej przemiany dla reakcji rozkładu szczawianu manganu.
Wykonanie ćwiczenia:
Spekol włączamy do sieci. Aparat powinien nagrzewać się minimum 30 minut przed rozpoczęciem pomiarów.
Nastawiamy długość fali 440 nm. Zerujemy przyrząd. Wkładamy kuwetę z cieczą wzorcową (wodą) w bieg wiązki światła, następnie wprowadzamy badaną próbkę w bieg wiązki światła. Odczytujemy ekstynkcję E. Sporządzamy roztwory wyjściowe reagentów. W tym celu 2 cm3 0.1 M roztworu MnSO4 mieszamy z 14 cm3 0.1 M roztworu H2C2O4 (roztwór 1). Do 8 cm3 tego roztworu wlewamy 2 cm3 0.01M KMnO4. Zmiana zabarwienia roztworu wynika z reakcji:
4 Mn+2 +MnO-4 +15 C2O4 -2 + 8H+ =5[Mn(C2O4)3]-3 +4 H2O
Po zmieszaniu roztworu 1 z 2 cm3 0.01 M KmnO4 (t=0) otrzymany roztwór szybko wlewamy do przygotowanej kuwety i mierzymy ekstynkcję roztworu, co 1minutę. Pomiary przerywamy, gdy wartość spadnie poniżej 0.1. Pierwszy pomiar E przeprowadzamy dla t=1 min. Serię pomiarów powtarzamy dla mniejszego stężenia reagentów. W tym celu pozostałe 8 cm3 roztworu 1 mieszamy z 1 cm3 roztworu KMnO4.
OPRACOWANIE WYNIKÓW:
Rozpad kompleksowego anionu szczawianu manganu przebiega według reakcji:
2[Mn(C2O4)3]-3 =2Mn+2 + 5 C2O4-2 +CO2
Z równania stechiometrycznego reakcji możemy przypuszczać, że reakcja rozpadu szczawianu manganu jest reakcją pierwszego rzędu, dlatego też sprawdzamy czy spełnione jest dla niej równanie kinetyczne dla reakcji pierwszorzędowych:
lnc0/c=k*t (1)
gdzie:c0 - stężenie początkowe kompleksu
c - stężenie kompleksu po czasie t
t - czas przebiegu reakcji w (sec)
k -stała szybkości reakcji
Kinetykę rozpadu barwnego anionu na bezbarwne produkty śledzimy metodą spekrtrofotometryczną przez pomiar ekstynkcji w czasie.
Ponieważ ekstynkcja E jest proporcjonalna do stężenia barwnych jonów w roztworze
E= ![]()
(2)
gdzie:
![]()
-molowy dziesiętny współczynnik ekstynkcji
d -grubość warstwy absorbującego roztworu
W równaniu 1 stężenie można zastąpić bezpośrednio mierzalną wartością E i równanie to przybierze wtedy postać:
lnE0/E=k*t (3)
gdzie:E0 -wartość ekstynkcji roztworu dla t=0
E -wartość ekstynkcji roztworu po czasie t [s]
Równanie (3) możemy przedstawić w formie wykładniczej
log E =log E0 -(k*t)/2.303 (4)
Z równania (4) możemy znaleźć wyrażenie na tzw. czas połówkowy reakcji, to znaczy czas po upływie, którego stężenie substratu spada do połowy jego stężenia początkowego.
![]()
=ln2/k (5)
Przy pomocy równania (3) możemy w prosty sposób sprawdzić czy reakcja rozpadu szczawianu manganu jest reakcją pierwszego rzędu.
W tym celu sporządzamy wykres zależności log E od t [s] dla każdej serii pomiarowej i metodą najmniejszych
Kwadratów określamy parametry równania 4. Wartość k obliczamy z nachylenia prostej log E=f(t) dla każdej serii,
Następnie wyznaczamy średnią wartość k oraz czas połowicznej przemiany ![]()
na podstawie równania 5.
t[s] |
E |
logE |
E2 |
log(E2) |
60 |
1,336 |
0,125806 |
0,681 |
-0,16685 |
120 |
1,248 |
0,096215 |
0,642 |
-0,19246 |
180 |
1,166 |
0,066699 |
0,603 |
-0,21968 |
240 |
1,092 |
0,038223 |
0,556 |
-0,25493 |
300 |
1,022 |
0,009451 |
0,512 |
-0,29073 |
360 |
0,958 |
-0,01863 |
0,468 |
-0,32975 |
420 |
0,898 |
-0,04672 |
0,422 |
-0,37469 |
480 |
0,832 |
-0,07988 |
0,382 |
-0,41794 |
540 |
0,788 |
-0,10347 |
0,343 |
-0,46471 |
600 |
0,736 |
-0,13312 |
0,306 |
-0,51428 |
660 |
0,689 |
-0,16178 |
0,273 |
-0,56384 |
720 |
0,645 |
-0,19044 |
0,242 |
-0,61618 |
780 |
0,604 |
-0,21896 |
0,214 |
-0,66959 |
840 |
0,567 |
-0,24642 |
0,188 |
-0,72584 |
900 |
0,53 |
-0,27572 |
0,164 |
-0,78516 |
960 |
0,495 |
-0,30539 |
0,142 |
-0,84771 |
1020 |
0,463 |
-0,33442 |
0,121 |
-0,91721 |
1080 |
0,431 |
-0,36552 |
0,105 |
-0,97881 |
1140 |
0,42 |
-0,37675 |
|
|
1200 |
0,375 |
-0,42597 |
|
|
1260 |
0,349 |
-0,45717 |
|
|
1320 |
0,325 |
-0,48812 |
|
|
1380 |
0,303 |
-0,51856 |
|
|
1440 |
0,281 |
-0,55129 |
|
|
1500 |
0,26 |
-0,58503 |
|
|
1560 |
0,242 |
-0,61618 |
|
|
1620 |
0,224 |
-0,64975 |
|
|
1680 |
0,207 |
-0,68403 |
|
|
1740 |
0,192 |
-0,7167 |
|
|
1800 |
0,177 |
-0,75203 |
|
|
1860 |
0,164 |
-0,78516 |
|
|
1920 |
0,152 |
-0,81816 |
|
|
1980 |
0,14 |
-0,85387 |
|
|
2040 |
0,129 |
-0,88941 |
|
|
2100 |
0,119 |
-0,92445 |
|
|
2160 |
0,109 |
-0,96257 |
|
|
2220 |
0,101 |
-0,99568 |
|
|
Obliczanie parametru a metodą najmniejszych kwadratów:
Roztwór1:
n=39
![]()
42180 ![]()
-640924
![]()
-15,195 ![]()
1779152400
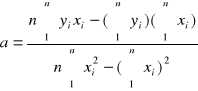
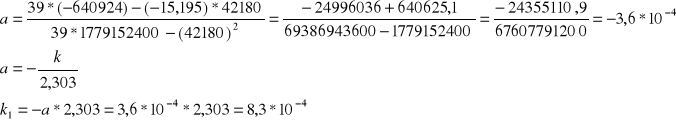
Roztwór2
n=18
![]()
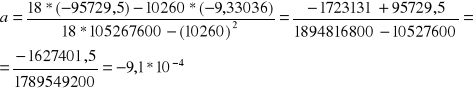
![]()
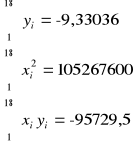
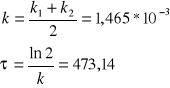
Wyszukiwarka
Podobne podstrony:
egz.40, II rok, zimowy, Chemia Fizyczna, zagadnienia do egzaminu
wyklad z czwartku chemia fizycz dnia19 marca
Chemia fizyczna sprawozdanie (6 1) id 112219
Chemia fizyczna wykład 11
chemia fizyczna38
chemia fizyczna07
chromatografia jonowymienna 2, Rok I, chemia fizyczna, chemia fizyczna-protokoły
10.6 poprawione, semestr 4, chemia fizyczna, sprawka laborki, 10.6
Pojęcia na egzamin z metali, Chemia Fizyczna, chemia fizyczna- laborki rozne, Rozne
Tabelka pomiarowa do 21, BIOTECHNOLOGIA POLITECHNIKA ŁÓDZKA, CHEMIA FIZYCZNA
CHEMIA FIZYCZNA- spektrografia sc, Ochrona Środowiska pliki uczelniane, Chemia
Kolokwium nr 2 (2), Technologia chemiczna, Chemia fizyczna, 3 semestr, fizyczna paczi
Chemia fizyczna 18, chemia fizyczna, chemia, FIZYCZNA - raporty
mmgg, Studia PŁ, Ochrona Środowiska, Chemia, fizyczna, laborki, wszy, chemia fizyczna cz II sprawka
Pytania z wejściówek, analityka medyczna UMP 2014, chemia fizyczna, ćwiczenia
raport5.2, UMK, Chemia fizyczna
więcej podobnych podstron