Paweł Detyna

II MiBM Gr. II

S P R A W O Z D A N I E

Temat:

Promieniotwórczość. Wyznaczanie masowego współczynnika pochłaniania promieniowania gamma dla różnych ciał.

WSTĘP:

Jądro atomowe zbudowane jest z nukleonów tzn. protonów i neutronów. Protony są to cząstki elementarnym e=1,6021*10^-19 C i masie spoczynkowej M_P =1,6748*10^-27 kg. Neutrony są to cząstki elementarne elektrycznie obojętne o masie spoczynkowej M_p=1,6748*10^-27kg Liczba protonów w jądrze charakteryzuje atom pierwiastka a mianowicie liczba protonów Z zwana liczbą atomową. Suma liczby protonów i neutronów w jądrze przedstawia liczbę masową A.

Defekt masy jądra czyli niedobór (masa jądra nie równa się sumie mas składników jest mniejsza od sumy mas składników).

Energia wiązania E=Δmc² Wzór ten przedstawia energię, która wyrażała się podczas łączenia się odpowiedniej liczby nukleonów w jądro atomowe. Wyrażamy ją w MeV . Dzieląc energię wiązania jądra przez liczbę tworzących go nukleonów znajdujemy energię wiązania 1 nukleonu tzn. ilość energii wyzwalanej podczas przyłączenia 1 nukleonu do jądra lub energii, jakiej należy dostarczyć, aby 1 nukleon usunąć z jądra.

Modele jądrowe atomu

I na początku XIX wieku

Modelowe przedstawienie atomu w tym okresie odpowiada kuli. W całej objętości tej kuli jest równomiernie rozłożony ładunek dodatni i masa. Wewnątrz kuli rozmieszczone są elektrony z zachowaniem pewnej symetrii. Elektrony mogą wykonywać ruchy drgające dokoła swoich położeń równowagi. Liczba elektronów w atomie jest taka że łączny ładunek elektryczny wynosi zero. Atom jako całość jest wiec elektrycznie obojętny.

II model Rutheforda

Atom zbudowany jest z jądra w którym skupia się całkowity ładunek dodatni i prawie cała masa atomu.

Liczba elektronów jest taka że ich łączny ładunek ujemny neutralizuje dodatni ładunek jądra.

Zjawisko promieniotwórczości polega na spontanicznej przemianie jąder atomowych danego pierwiastka w jądra atomowe innego pierwiastka z równoczesnym wypromieniowaniem cząstek α i β. Rozpadowi temu towarzyszy najczęściej promieniowanie natury elektromagnetycznej zwane promieniowaniem γ. Promieniowanie naturalne sprowadza się do przemian zachodzących w jądrach pierwiastków cięższych począwszy od Z=81 do Z=92. Zmiany zachodzące w jądrach pierwiastków promieniotwórczych naturalnych dzielimy na przemiany α i β. Promieniowanie α jest to emisja jąder helu, w wyniku której jądra pierwiastka promieniotwórczego przekształcają się w jądra innego pierwiastka. ^A_ZX→_Z-2^A-4Y+₂⁴He podczas emisji cząstki α pierwiastek przesuwa się o dwa miejsca w układzie okresowym do tyłu. Emisja cząstek β związana jest z przemianami nukleonów w jądrach i pierwiastkach promieniotwórczych. W przypadku rozpadu β^- w jądrze atomowym zachodzi przemiana neutronu w proton.

a w rozpadzie β⁺ protonu w neutron

Przy promieniowaniu β możemy mieć do czynienia z promieniowaniem β^- (emisja elektronów ) i β⁺ (emisja pozytonów).

Podczas emisji cząstek β^- pierwiastek przesuwa się o jedno miejsce do przodu w układzie okresowym.

Podczas emisji cząstek β⁺ pierwiastek przesuwa się o jedno miejsce do tyłu w układzie okresowym.

PRAWO ROZPADU PROMIENIOTWÓRCZEGO.

Prawo rozpadu promieniotwórczego stwierdza że liczba jąder izotopów promieniotwórczych rozpadająca się w jednostce czasu jest proporcjonalna do całkowitej liczby istniejących jąder. N=N_oe^-λt

N-liczba jąder w chwili t

N₀-liczba jąder w chwili t=0

λ-stała rozpadu

Istnieje także czas t=T po upływie którego liczba jąder danego izotopu promieniotwórczego zmniejsza się o połowę.

CZĘŚĆ PRAKTYCZNA:

Tabela nr 1:

Nr	1	2	3	4	5	6	7	8	9	10
I'T	121	100	109	91	88	104	115	92	115	102
I'0	2978	2947	2973	2971	2998
IT - śr	103,7
Io - śr	2973,4

Nr Ciała	Nr pomiaru	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10
ołów	I'1	2243	1500	960	759	549	402	276	258	178	152
		I'2	2154	1507	980	739	514	453	294	246	204	138
		I'3	2182	1551	988	782	554	366	304	259	181	191
		I'4	2236	1480	997	766	545	427	274	228	176	147
		I1...n	2203,75	1509,5	981,25	761,5	540,5	412	287	247,75	184,75	157
Nr Ciała	Nr pomiaru	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10
stal	I'1	2421	2032	1706	1445	1202	989	827	709	633	518
		I'2	2602	2128	1707	1519	1191	996	870	722	619	572
		I'3	2463	2026	1716	1467	1183	980	826	726	616	529
		I'4	2501	2121	1710	1466	1227	1018	859	748	616	532
		I1...n	2286,75	1893,25	1592	1337,5	1098,25	920,625	785,875	673,625	579,38	537,75
Nr Ciała	Nr pomiaru	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10
mosiądz	I'1	2619	2398	2131	1895	1708	1456	1339	1145	980	897
		I'2	2658	2374	2073	1919	1696	1547	1250	1226	1009	922
		I'3	2681	2397	2047	1866	1670	1502	1299	1177	1030	874
		I'4	2678	2443	2075	1853	1723	1512	1263	1187	1003	935
		I1...n	2659	2403	2081,5	1883,25	1699,25	1504,25	1287,75	1183,75	1005,5	907

	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10
d - ołów	2,953	5,766	9,776	12,976	17,089	20,182	24,645	27,725	32,108	35,151
d - stal	4,4	8,826	13,226	17,632	22,025	26,428	30,811	35,214	39,614	44,01
d - mosiądz	2,37	4,613	7,273	9,959	12,622	15,255	17,888	20,881	23,897	26,88
I1...n średnie	ołów		728,5
		stal		1170,5
		mosiądz		1661,425

d_o
8,9 mm

d_s
23 mm

d_m
22 mm

Pomiar współczynnika pochłaniania:

Ołów -

Stal -

Mosiądz -

- ołów

- stal

- mosiądz

Współczynnik
wyznaczamy z równania:

gdzie I₀ wyznaczyliśmy na początku ćwiczenia (dane w tabelce nr. 1)

I₀ = 2973,4

I - jest to średnia wartość odczytywana z miernika.

Wartość x (w naszym przypadku d - grubość ciała pochłaniającego) odczytywaliśmy z wykresu ln(I_o/I_1…n)=f(d). Jest to liniowa zależność dzięki temu wyznaczana grubość dla wartości logarytmu równej 1 jest dość dokładna. Wartość tą podstawiliśmy do powyższego równania skąd obliczaliśmy współczynnik pochłaniania.

wyznaczaliśmy ze wzoru:

gdzie:

- obliczony współczynnik

- gęstość bezwzględna [kg/m³]

	[kg/m^3]
stal	7800	0,04	0,000020260353
ołów	11300	0,158	0,000003587053
mosiądz	8400	0,026	0,000003149515

RACHUNEK BŁĘDÓW:

=

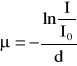
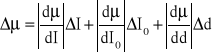
Błędy podane są w tabelce:

I	d [mm]	ln (I/I0)
2203,8	2,953	-0,29955	0,003569	4,01867E-05	0,003609
1509,5	5,766	-0,67793	0,002421	0,000113782	0,002535
981,25	9,776	-1,10863	0,002156	0,00029635	0,002453
761,5	12,976	-1,36217	0,002513	0,00050675	0,00302
540,5	17,089	-1,70497	0,003746	0,000940159	0,004686
412	20,182	-1,97644	0,005384	0,001456582	0,00684
287	24,645	-2,33798	0,008972	0,002553329	0,011525
247,75	27,725	-2,48504	0,011514	0,00332748	0,014841
184,75	32,108	-2,77846	0,017649	0,005167547	0,022816
157	35,151	-2,94122	0,022627	0,00665722	0,029284

Dla ołowiu

I	d [mm]	ln (I/I0)
2286,8	2090	-0,26257	0,091396	0,027175712	0,118572
1893,3	1742,625	-0,45141	0,092044	0,027368394	0,119413
1592	1464,75	-0,62471	0,092007	0,027357334	0,119364
1337,5	1217,875	-0,7989	0,091056	0,027074613	0,118131
1098,3	1009,438	-0,99599	0,091913	0,027329492	0,119243
920,63	853,25	-1,17241	0,092682	0,027557948	0,12024
785,88	729,75	-1,33066	0,092859	0,027610481	0,120469
673,63	626,5	-1,48479	0,093005	0,027653889	0,120659
579,38	558,5625	-1,63551	0,096408	0,028665885	0,125074
537,75	537,75	-1,71007	0,100001	0,029734	0,129735

Dla stali

I	d [mm]	ln (I/I0)
2659	2,37	-0,11176	0,002079	2,67013E-05	0,002105
2403	4,613	-0,21299	0,001193	5,718E-05	0,00125
2081,5	7,273	-0,35662	0,001024	0,000103961	0,001128
1883,3	9,959	-0,45671	0,000989	0,000157285	0,001147
1699,3	12,622	-0,55952	0,001094	0,000220899	0,001315
1504,3	15,255	-0,68141	0,001307	0,00030157	0,001609
1287,8	17,888	-0,83681	0,001651	0,000413058	0,002064
1183,8	20,881	-0,92102	0,001975	0,00052452	0,0025
1005,5	23,897	-1,08422	0,002566	0,000706686	0,003273
907	26,88	-1,18732	0,003128	0,000881218	0,004009

Dla mosiądzu

4

---