Tomasz Kowalski

Wykłady z matematyki dla studentów kierunków ekonomicznych

Wykład 21

KOMBINATORYKA. PRAWDOPODOBIEŃSTWO ZDARZEŃ - lista zadań

1. Obliczyć: a)
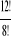
   , b)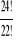
   , c)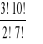
   , d)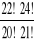
   , e)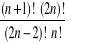
   , f)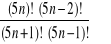
   .
   

2. Z cyfr: 1, 2, 3, 4, 5 tworzymy liczby pięciocyfrowe. Ile jest takich liczb? Jak zmieni się wynik, jeżeli jedną z cyfr zastąpimy cyfrą 0?
   

3. Na półce z książkami znajdują się 4 książki z matematyki i 5 książek z logiki.
   a) Ile jest sposobów rozmieszczenia tych książek?
   b) Ile jest sposobów rozmieszczenia, w których książki z matematyki „przeplatają się” z książkami      z logiki.
   

4. Ile jest liczb czterocyfrowych utworzonych z cyfr 1, 2, 3, 4, 5, 6, w których nie powtarza się żadna cyfra?
   

5. Ile można utworzyć liczb sześciocyfrowych z cyfr 4, 5, 6? Cyfry mogą się powtarzać.
   

6. W grze liczbowej losuje się 5 liczb z 40. Ile jest możliwych wyników?
   

7. Ile nastąpi powitań gdy spotka się 6 znajomych?
   

8. Ile można wykonać różnych trójkolorowych chorągiewek z sześciu barw? (kolejność jest istotna).
   

9. Na ile sposobów może ubrać się pani posiadająca 3 różne kapelusze, 5 różnych sukni i 3 pary różnych pantofli?
   

10. Na płaszczyźnie narysowano 9 punktów tak, aby żadne trzy nie były współliniowe. Ile prostych można poprowadzić łącząc te punkty?
    

11. Ile różnych płaszczyzn można poprowadzić przez 5 różnych punktów, z których żadne cztery nie leżą w jednej płaszczyźnie?
    

12. Ile można uzyskać różnych anagramów słowa a) MORELA? b) BARBAKAN?
    

13. W turnieju szachowym każdy uczestnik rozgrywa z każdym z pozostałych jedną partię. Łącznie rozegrano 45 partii. Ilu było uczestników?
    

14. Obliczyć, ile jest liczb czterocyfrowych, w których nie powtarza się żadna cyfra?
    

15. Mamy 8 ponumerowanych kul, które rozmieszczamy losowo w 3 szufladach. Ile jest różnych rozmieszczeń tych kul?
    

16. Alfabet Morse`a składa się z dwóch różnych elementów: kreski i kropki. Ile znaków pisarskich można zakodować przy pomocy tych elementów, jeśli każdy znak składa się z co najwyżej 5 elementów?
    

17. Na parterze 7-pietrowego bloku wsiadło do windy 6 pasażerów. Na ile sposobów mogą wysiąść, jeśli a) wysiadają na dowolnych piętrach, b) każdy wysiada na innym piętrze?

18. Z talii 52 kart losowo wybieramy 5 kart. Na ile sposobów można wśród nich uzyskać
    a) 3 asy, b) 3 asy i jednego króla, c) 3 karty jednej wartości, d) 2 asy ?
    

19. Rzucamy kolejno trzema monetami. Jakie jest prawdopodobieństwo, że za każdym razem wypadła ta sama strona monety?
    

20. Rzucamy dwiema kostkami do gry. Obliczyć prawdopodobieństwo, że

a) na pierwszej kostce wypadło co najwyżej tyle oczek, co na kostce drugiej,

b) w sumie wypadło mniej niż 7 oczek, c) suma oczek jest podzielna przez 4.

21. Z talii 24 kart losujemy jednocześnie 3 karty. Jakie jest prawdopodobieństwo, że wśród nich:

a) jest dokładnie jeden as, b) są co najmniej dwie damy, c) jest mariasz (król i dama tego samego     koloru).

22. Dwudziestoosobowa grupa studencka, w której jest 6 kobiet otrzymała 4 bilety do teatru. Bilety rozdziela  się drogą losowania. Jakie jest prawdopodobieństwo, że wśród posiadaczy biletów:

a) będzie dwóch mężczyzn i dwie kobiety, b) będą sami mężczyźni?

23. W celu kontroli jakości partii towaru złożonej ze 100 sztuk losuje się 5 z nich. Jeśli choć jedna z tych sztuk jest wadliwa towar nie zostaje przyjęty. Jakie jest prawdopodobieństwo odrzucenia partii towaru, jeżeli zawiera ona 7 sztuk wadliwych?
    

24. Z grupy składającej się z dziesięciu kobiet i pięciu mężczyzn wybrano w sposób losowy delegację 3-osobową. Jakie jest prawdopodobieństwo, że w skład delegacji wchodzą mężczyźni i kobiety?
    

25. W kolejce ustawiło się 12 osób. Obliczyć prawdopodobieństwo, że między dwoma ustalonymi będą stały trzy.
    

26. Autobus, którym jedzie 6 osób zatrzymuje się na 9 przystankach. Jakie jest prawdopodobieństwo, że każdy pasażer wysiądzie na innym przystanku?
    

27. Losujemy dwie liczby z przedziału
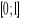
    . Jakie jest prawdopodobieństwo, że ich suma nie przekracza 0,5 ?
    

28. Wyznaczyć prawdopodobieństwo, ze pierwiastki równania kwadratowego x² + 2ax + b = 0 są rzeczywiste, jeżeli współczynniki mogą przyjąć z jednakowym prawdopodobieństwem każdą z wartości w kwadracie:
    .
    

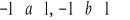
29. Na płaszczyźnie poprowadzono dwie rodziny prostych równoległych, które dzielą ją na prostokąty o bokach a i b,
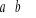
    . Na płaszczyznę tę rzucono w sposób losowy monetę o średnicy 2r < a. Obliczyć prawdopodobieństwo, ze nie przetnie ona żadnej z prostych.
    

30. Losujemy trzy liczby: x, y, z z odcinka
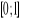
    . Jakie jest prawdopodobieństwo, że:
    a)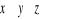 
    ,        b)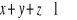
    ?
    

31. Z przedziału [0; 4] wybieramy losowo liczby x i y. Obliczyć prawdopodobieństwo, że:
    a)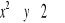
    , b)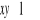
    .
    

32. Wybieramy losowo punkt (x, y) kwadratu
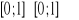
    . Obliczyć prawdopodobieństwo, że:
    a)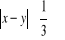
    ,    b)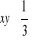
    , c)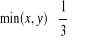
    , d)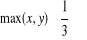
    , e)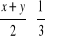
    .
    

Odpowiedzi

1. a) 11 880, b) 552, c) 2160, d) 5 610 526, e)
, f)
.

2. 120, 96. 3. a) 9! = 362 880, b)
. 4. 360. 5.
. 6. 6 580 080.

7. 15. 8. 120. 9. 45. 10. 36. 11. 10. 12. a) 720, b) 3360. 13.
. 14. 4536.

15.
. 16. 62. 17. a) 117 649, b) 5 040. 18. a) 4 512, b) 704, c) 58 656, d) 233 496.

19.
. 20. a)
, b)
, c)
. 21. a)
, b)
, c)
. 22. a)
, b)
.

23. 0,31. 24.
. 25.
. 26.
. 27.
. 28.
. 29.
.

30. a)
, b)
. 31. a)
, b)
. 32. a)
, b)
, c)
, d)
, e)
.

2

Zadania do wykładu 21: Kombinatoryka. Prawdopodobieństwo zdarzeń.

2

---