Jeżeli na ciało działa siła i nie jest ona zrównoważona inną siłą, to nadaje temu ciału przyspieszenie wprost proporcjonalne do działającej siły ( II zasada dynamiki Newtona)
a ![]()
F
z czego wynika, że stosunek siły do przyspieszenia jest wielkością stałą dla danego ciała. Stosunek ten oznaczamy m i nazywamy masą ciała.
![]()
.Stała siła nadaje ciału stałe przyspieszenie, czyli powoduje ruch jednostajnie zmienny. Można wtedy przyspieszenie definiować :
![]()
Gdy F ≠ const, to również a ≠ const i wówczas interesuje nas przyspieszenie średnie oraz przyspieszenie chwilowe określane wzorem
![]()
lub a = ![]()
, czyli a jest pochodna prędkości względem czasu
Przyspieszenie jest wielkością wektorową. Kierunek zwrot przyspieszenia jest zgodny z kierunkiem i zwrotem siły. Przyspieszenie może mieć również wartość ujemną- opóźnienie.
Każde ciało znajduje się w polu grawitacyjnym innych ciał. Przyciąganie grawitacyjne jest z reguły znikomo małe w stosunku do działających równocześnie innych sił. Jest ono równoważone przez te siły
Ciężar ciała- siła grawitacji między dowolnym ciałem a Ziemią. Wyraża się za pomocą II zasady dynamiki następująco:
F' = mg'
Na wartość przyspieszenia w różnych punktach Ziemi wpływają
- kształt Ziemi
- ruch obrotowy Ziemi dokoła własnej osi
- niejednorodność budowy Ziemi
Ziemia ma swoisty kształt tzw. geoidy, przypominający elipsoidę obrotową spłaszczoną od strony biegunów. Dzięki temu wartość g rośnie w miarę wzrostu szerokości geograficznej
Każde ciało znajdujące się na Ziemi uczestniczy w jej ruchu obrotowym dookoła osi. Potrzebna do utrzymania ciała w tym ruchu siła dośrodkowa jest proporcjonalna do promienia zakreślanego koła, a więc największa na równiku, a najmniejsza na biegunie. Stąd wniosek, że ruch obrotowy Ziemi dokoła własnej osi wpływa na wartość g w ten sposób, że rośnie ono stopniowo w miarę przesuwania się wzdłuż południka od równika do bieguna.
Niejednorodność struktury Ziemi, jak również ukształtowanie powierzchni Ziemi powodują niewielkie wahania wartości g.
Ogólny wzór określający wartość siły grawitacji, zwany prawem powszechnego ciążenia
F = ![]()
Jest słuszny dla mas punktowych oraz ciał kulistych z równomiernym rozkładem masy
g = G![]()
Z tego wzoru wynika że nie zależy ono od masy ale w dużym stopniu od odległości środków mas (Ziemi)
Dokładne wyznaczenie przyspieszenia ziemskiego różnych szerokościach geograficznych na różnych poziomach ma znaczenie np. w określeniu kształtu Ziemi.. Jednym z najprostszych dość dokładnych sposobów wyznaczenia wartości g jest metoda wahadła matematycznego lub fizycznego.
Wahadło fizyczne- bryła sztywna mogąca wykonywać obroty dookoła poziomej osi przechodzącej przez dowolny punkt tej bryły poza jego środkiem ciężkości.
Odległość środka ciężkości S wahadła od osi obrotu O równa się długości wektora wodzącego środka ciężkości d = ![]()
. Gdy wahadło wychylimy o kąt α, to działa na nie względem osi obrotu O moment siły ciężkości, równy liczbowo mgdsinα, skierowujący wahadło w stronę położenia równowagi, co uwzględniamy traktując moment jako wartość ujemną.
![]()
×![]()
×![]()
Zgodnie z równaniem ruchu obrotowego bryły sztywnej zewnętrzny moment siły ![]()
nadaje bryle przyspieszenie kątowe proporcjonalne do zewnętrznego momentu siły, zgodnie z nim skierowane, a odwrotnie proporcjonalne do momentu bezwładności
I 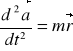
×![]()
Moment siły ciężkości ma przeciwny zwrot do drogi kątowej. Wektor drogi kątowej ![]()
Ma wartość α, natomiast kierunek i zwrot jest określony regułą śruby prawoskrętnej. Stąd
I ![]()
, wprowadzając oznaczenie ![]()
otrzymamy równanie różniczkowe ruchu wahadła fizycznego dla dowolnych kątów
wychylenia α
![]()
W przybliżeniu dla małych kątów sinα ≈ α otrzymamy równanie różniczkowe oscylatora
harmonicznego
![]()
Jeśli w czasie t=0 kąt wychylenia wahadła wynosi α0 rozwiązanie ma postać
![]()
natomiast okres drgań dla małych kątów wychylenia wynosi
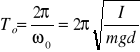
Długość zredukowana wahadła fizycznego- długość wahadła matematycznego mającego ten sam okres wahań, a więc spełniającego warunek
Ffiz =Fmat
To = 2![]()
z porównaia wzorów mamy ![]()
Długość zredukowana wahadła fizycznego, a tym samym jego okres To , zależy od długości d osi obrotu O od środka ciężkości S.
Zgodnie z twierdzeniem Steinera: moment bezwładności bryły I względem dowolnej osi jest równy sumie momentu bezwładności Ic tej bryły względem osi równoległej do danej i przechodzącej przez środek masy bryły oraz iloczynu masy bryły i kwadratów odległości między wymienionymi osiami
I = Is+ md2
Stąd wzór ma postać:
![]()
Jest to równanie kwadratowe ze względu na d o postaci
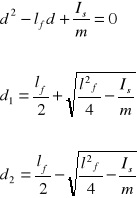
Dla jednej długości zredukowanej istnieją dwie odległości środka od osi obrotu. Przy tych odległościach okresy drgań wahadła fizycznego są sobie równe.
Gdy znajdziemy takie osie obrotu wahadła fizycznego, względem których okresy drgań będą równe, to suma odległości tych osi od środka ciężkości będzie się równać długości zredukowanej wahadła fizycznego. Powyższe twierdzenie ma zastosowanie w wahadle rewersyjnym. Najczęściej spotykaną formą wahadła rewersyjnego jest stalowy pręt, na którym znajdują się trzy metalowe ciężarki w postaci trzech soczewek A, B, C.
Dwie z nich A i B są nieruchome, trzecią C możemy przesuwać wzdłuż pręta. Osie obrotu O1 i O2 stanowią ostrza pryzmatów, na których podparte jest wahadło. Odległość między ostrzami pryzmatów wynosi l. Przesuwając soczewkę C znajdziemy takie położenie środka ciężkości wahadła, przy którym okresy wahań na osiach O1 i O2 będą jednakowe. Środek ciężkości S tego wahadła leży między osiami O1 i O2. Suma odległości środka ciężkości od tych osi obrotu będzie równa odległości l między osiami obrotu. Odległość między osiami obrotu będzie w tym przypadku równa długości zredukowanej wahadła fizycznego lf. Znając wartość długości zredukowanej lf i okres wahań To można wyznaczyć wartość przyspieszenia ziemskiego
g = ![]()
Najistotniejszą poprawką przy wyznaczaniu przyspieszenia ziemskiego za pomocą wahadła rewersyjnego jest zależność okresów drgań T wahadła od amplitudy wychylenia ![]()
. Dla dużych kątów wychylenia ruch wahadła jest ruchem okresowym, ale nie jest ruchem harmonicznym. Dla dowolnych kątów wychylenia α spełnione jest równanie
![]()
Okres drgań w tym przypadku jest dłuższy niż dla małych wychyleń wynosi
T = 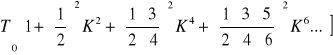
K= sin![]()
Jeśli w tym wzorze na okres T uwzględnimy przybliżenie drugiego wyrazu sumy, to po uwzględnieniu zależności K= sin![]()
otrzymamy 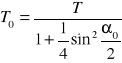
Wyszukiwarka
Podobne podstrony:
Lab. przysp. ziemskie, Fizyka
Fizyka Laborka temat 1 Pomiar przyśpieszenia ziemskiego metodą?ssela
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła pros, Fizyka
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, 101B , Fizyka 101
Fizyka& wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
Fizyka- Pomiar przyspieszenia ziemskiego ziemskiego zahadłem, ĆWICZENIE NR1
cw 10 - Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, Sprawozdania jakieś, F
Wyznaczanie przyspieszenia ziemskiego-beny, Fizyka-Sprawozdania
Metoda pomiaru przyspieszenia ziemskiego, Sprawozdania - Fizyka
Wyznaczanie przyspieszenia ziemskiego za pomoca wahadła matematycznego, studia, fizyka
fizyka Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego, budownictwo, semestr
więcej podobnych podstron