SPRAWOZDANIE Z LABORATORIUM Z FIZYKI

ĆWICZENIE NR. 1

WYZNACZANIE SZEROKOŚCI SZCZELIN, STAŁYCH SIATEK DYFRAKCYJNYCH I DŁUGOŚCI FALI SPRĘŻYSTEJ.

SEKCJA VI:

MARCIN CHOLEWA

STANISŁAW WAWSZCZAK

Odległość siatki dyfrakcyjnej od fotoogniwa ustawionego w miejscu zerowego prążka dyfrakcyjnego wynosi:

l = 20 [cm]

TABELA POMIARÓW

POMIAR NR. 1 POMIAR NR. 2 POMIAR NR. 3

PRĄŻKI	Napięcie [mV] U	Odległość od m0 [cm] bm	Napięcie [mV] U	Odległość od m0 [cm] bm	Napięcie [mV] U	Odległość od m0 [cm] bm
m0	114	0	112	0	114	0
m1	101, 5	2, 4	109	2, 5	112	2, 3
m2	59, 6	5, 0	61	5, 1	63	4, 9
m3	16, 5	7, 9	18, 8	8, 0	16, 6	7, 8
m4	90, 5	2, 3	101	2, 4	88	2, 2
m5	56, 6	4, 9	49	5, 0	56	4, 8
m6	20, 9	7, 8	12, 2	7, 9	13, 3	7, 7

Obliczam wartości średnie położeń m- tego prążka, oraz wartości średnie napięć korzystając ze wzoru:

_śr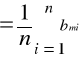

_śr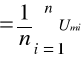

gdzie n = 3

TABELA WARTOŚCI ŚREDNICH

PRĄŻKI	ŚREDNIE NAPIĘCIE [mV] Uśr	ŚREDNIA ODLEGŁOŚĆ [cm] bmśr
m0	113, 33 [mV]	0, 0 [cm]
m1	104, 17 [mV]	2, 4 [cm]
m2	61, 20 [mV]	5, 0 [cm]
m3	17, 30 [mV]	7, 9 [cm]
m4	93, 17 [mV]	2, 3 [cm]
m5	53, 87 [mV]	4, 9 [cm]
m6	15, 47 [mV]	7, 8 [cm]

Odchylenia standardowe dla wartości średnich napięć:

Dla n = 3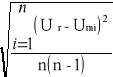

PRĄŻKI	Odchylenia standardowe Uśr [mV]
m0	0, 67 [mV]
m1	3, 92 [mV]
m2	0, 99 [mV]
m3	0, 75 [mV]
m4	3, 98 [mV]
m5	2, 44 [mV]
m6	2, 74 [mV]

Odchylenia standartowe dla wartości średnich odległości:

Dla , n = 3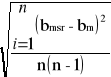

PRĄŻKI	Odchylenie standardowe bmśr [cm]
m0	0, 000 [cm]
m1	0, 058 [cm]
m2	0, 058 [cm]
m3	0, 058 [cm]
m4	0, 058 [cm]
m5	0, 058 [cm]
m6	0, 058 [cm]

Metodą różniczki zupełnej obliczam niepewność tego wyniku:

Dla b₁:

f(x, y, z) =
x = 2, 4 x₀= 2 Δx = 0, 4

y = 2, 5 y₀= 2 Δy = 0, 5

z = 2, 3 z₀= 2 Δz = 0, 3

df(x₀, y₀, z₀) =

=

=

=

df(2, 2, 2) =
0, 4 +
0, 5 +
0, 3 = 0, 396 [ cm ]

Niepewność tego wyniku wynosi dla

b₁ = ± 0, 396 [ cm ]

b₂ = ± 0, 000 [ cm ]

b₃ = ± 0, 100 [ cm ]

b₄ = ± 0, 297 [ cm ]

b₅ = ± 0, 100 [ cm ]

b₆ = ± 0, 198 [ cm ]

DANE DO WYKRESU ZALEŻNOŚCI ILOCZYNU RZĘDU PRĄŻKA I DŁUGOŚCI FALI ŚWIATŁA OD SINUSA KĄTA UGIĘCIA ŚWIATŁA DLA DANEGO PRĄŻKA DYFRAKCYJNEGO.

gdzie λ = 0, 6328 ⋅ 10 ^-6 [ m ]

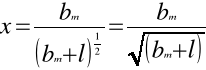
[ 1 ]

m	y	x
0	0, 0000 ⋅ 10^-6 [ m ]	0, 000 [ 1 ]
1	0, 6328 ⋅ 10^-6 [ m ]	0, 507 [ 1 ]
2	1, 2656 ⋅ 10^-6 [ m ]	1, 000 [ 1 ]
3	1, 8984 ⋅ 10^-6 [ m ]	1, 496 [ 1 ]
4	2, 5312 ⋅ 10^-6 [ m ]	0, 487 [ 1 ]
5	3, 1640 ⋅ 10^-6 [ m ]	0, 982 [ 1 ]
6	3, 7968 ⋅ 10^-6 [ m ]	1, 480 [ 1 ]

Metodą najmniejszych kwadratów aproksymujemy wykres zależności y od x.

Dla n = 7

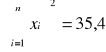
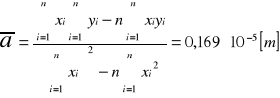
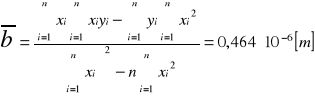
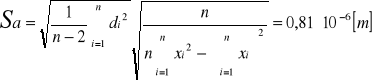
Prosta aproksymująca ma postać:

Wyznaczamy stałą siatki dyfrakcyjnej przez porównanie równania prostej aproksymującej z równaniem:

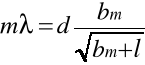
gdzie

WNIOSKI:

Dokładność wykonanych pomiarów uwarunkowana była dokładnością dysponowanego przez nas sprzętu. Błędy jakie mogą wystąpić są spowodowane niedokładnością odczytu z przyrządów mierniczych jak również niedokładnością ludzkich zmysłów.

Zarówno na siatce dyfrakcyjnej jak i na szczelinie prążki będące obrazem przepuszczalnego przez nie światła laserowego są w takiej samej odległości od prążka zerowego z lewej jak i z prawej strony.

Natężenie światła rejestrowanego przez fotoogniwo największe w prążku zerowym. Im dalej od prążka zerowego zarówno w lewo jak i w prawo natężenie światła w prążkach maleje.

---