Politechnika Śląska Wydział Elektryczny Laboratorium automatyki i sterowania	Studia Dzienne Inżynierskie 2004 / 2005 rok Semestr: VI
Temat ćwiczenia: Modelowanie układów regulacji. Badanie w dziedzinie częstotliwości
Studenci: Chropacz Paweł Motyka Ryszard Sawczuk Grzegorz Wyputa Piotr	Data wykonania: 28.02.2005r. Grupa: KSS 2/mgr Sekcja: 2 Prowadzący: dr inż.

1. Wstęp teoretyczny:

Transmitancja- funkcja charakteryzująca właściwości dynamiczne układu liniowego o skupionych i stałych parametrach (np. czwórnika elektr., układu regulacji automatycznej); określa zależność między sygnałem wejściowym (pobudzeniem), a sygnałem wyjściowym (odpowiedzią) układu; jest równa stosunkowi transformaty Laplace'a sygnału wyjściowego do transformaty sygnału wejściowego przy zerowych warunkach początkowych; postać transmitancji zależy tylko od parametrów układu i nie zależy od sygnałów.

O takiej transmitancji mówimy, że jest to transmitancja operatorowa.
Natomiast transmitancją widmową T(jw) liniowego układu stacjonarnego nazywać będziemy wielkość określoną jako stosunek wartości zespolonej składowej wymuszonej odpowiedzi Y(j) wywołanej wymuszeniem sinusoidalnym do wartości tego wymuszenia U(j):

Transmitancja widmowa T(j) z transmitancją operatorową układu ciągłego jest związana zależnością:
T(j) = T(s)|_s=j

co wynika bezpośrednio z definicji transmitancji operatorowej oraz transmitancji widmowej. Wartość funkcji T(j ) jest wielkością zespoloną zależną od parametrów układu oraz od pulsacji wymuszenia :
T(j )=P( )+jQ( ).
Przy czym
P( ) := Re T(j ), Q( ) := Im T(j ),
gdzie:
P( ) - charakterystyka rzeczywista,
Q( ) - charakterystyka urojona,
A( ) - moduł transmitancji widmowej - charakterystyka amplitudowa,
 ( ) - argument transmitancji widmowej - charakterystyka fazowa.

Charakterystykami częstotliwościowymi nazywamy krzywe przedstawiające transmitancję widmową T(j ) w funkcji pulsacji.
Między charakterystykami zachodzą związki jak między liczbami zespolonymi, a więc:

Oraz można wykazać, że część rzeczywista P( ) transmitancji widmowej T(j ) jest funkcją parzystą  , a część urojona Q( ) - funkcją nieparzystą tej pulsacji  :

P(- ) = P( ), Q(- ) = -Q( ).

Najczęściej spotykane rodzaje charakterystyk to:

• charakterystyka amplitudowo-fazowa (charakterystyka Nyquista),

• logarytmiczne; charakterystyka częstotliwościowa amplitudowa oraz charakterystyka częstotliwościowa fazowa zwane charakterystykami Bodego

Charakterystyka Nyquista jest wykresem transmitancji widmowej we współrzędnych zespolonych (P,Q).
T(j)=P()+jQ()

Amplitudę odczytujemy jako odległość danego punktu charakterystyki od środka układu współrzędnych.

Charakterystyki Bodego są charakterystykami logarytmicznymi. Tą nazwą obejmujemy dwie charakterystyki.
Logarytmiczna charakterystyka modułu - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy pulsację w skali logarytmicznej, a na osi rzędnych moduł M( ) transmitancji widmowej G(j ) wyrażony w decybelach odkładamy na skali liniowej

M( )|_[dB] = 20 log ( |G(j )| ) = 20 log A( )

Logarytmiczna charakterystyka fazy - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy również pulsację w skali logarytmicznej, a na osi rzędnych faza  ( ) w skali liniowej wyrażoną w stopniach

 ( ) = arg [G(j )].

Charakterystyki te łącznie w pełni opisują liniowy układ dynamiczny. Charakterystyki Bodego mają tę zaletę, iż można je łatwo przedstawić za pomocą asymptot. Taka przybliżona charakterystyka zwana charakterystyką asymptotyczną jest linią łamaną składającą się z odcinków asymptot charakterystyki rzeczywistej. Prostota polega na tym, że w transmitancjach widmowych występuje kilka typowych wyrażeń o charakterystycznym rozłożeniu zer i biegunów i można do nich stosować kilka prostych reguł.

1. Cel ćwiczenia:

Podstawowym celem ćwiczenia jest zapoznanie się z metodami badania układów regulacji w dziedzinie częstotliwości. W tym celu wyznaczaliśmy charakterystyki częstotliwościowe NYQUISTA i BODEQO poszczególnych bloków układów, przy pomocy programu symulacyjnego CC. Przy tym będziemy obserwować wpływ transmitancji poszczególnych bloków funkcjonalnych na zachowanie się układu w stanie pracy i kształtu przebiegu charakterystyk.

2. Przebieg ćwiczenia:

Schemat układu zamkniętej regulacji badanego w ćwiczeniu:

Ćwiczenie nr 1

Wyznaczenie transmitancji regulatora K_R1(s) w układzie zamkniętym oraz transmitancji K_OTW1(s) układu otwartego, przy następujących transmitancjach zadanych:

• K₀₁(s) =
  ,

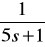
• K_Z1(s) =
  .

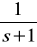
Na podstawie schematu układu regulacji zamieszczonego w punkcie nr 3 wyznaczamy szukane transmitancje korzystając z poniższych zależności:

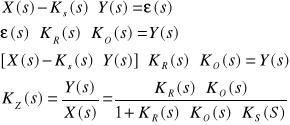
Odpowiednio transmitancje wynoszą:

Na podstawie schematu 2 umieszczonego w punkcie numer 3:

Po podstawieniu do wzorów otrzymujemy:

,

.

Korzystając z programu symulacyjnego CC otrzymujemy następujące charakterystyki częstotliwościowe naszych transmitancji:

• Charakterystyka Bodego dla transmitancji regulatora K_R1(jω):

• Charakterystyka Bodego dla transmitancji układu otwartego K_OTW1(jω):

• 
  Charakterystyki Bodego dla transmitancji układu zamkniętego K_Z1(jω) oraz obiektu K_O(jω)

• Charakterystyka Nyquista transmitancji regulatora K_R1(jω):

• Charakterystyka Nyquista transmitancji układu otwartego K_OTW1(jω):

• Charakterystyka Nyquista transmitancji obiektu K_O1(jω) i transmitancji układu zamkniętego K_Z1(jω):

Ćwiczenie nr 2:

Dla wyznaczonej transmitancji regulatora i zadanych transmitancji obiektów szukamy transmitancji układu zamkniętego:

a)

• K_02a(s) =
  ,

• 
  

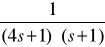
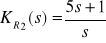
Transmitancje szukane:

• 
  
  

• 
  
  

• Charakterystyka Bodego transmitancji układu zamkniętego i otwartego:

• Charakterystyka Bodego transmitancji układu zamkniętego i obiektu:

• Charakterystyka Nyquista transmitancji układu zamkniętego i obiektu:

b)

• K_02b(s) =
  ,

• 
  

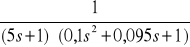
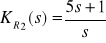
Transmitancje szukane:

• 
  
  

• 
  
  

• Charakterystyka Bodego transmitancji układu zamkniętego:

• Charakterystyka Bodego transmitancji układu otwartego:

• Charakterystyka Bodego transmitancji obiektu i układu zamkniętego:

• Charakterystyka Nyquista transmitancji obiektu:

• Charakterystyka Nyquista transmitancji układu zamkniętego:

Ćwiczenie nr 3:

Przyjmując następujące transmitancje:

• K₀₃(s) =
  ,

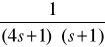
• K_Z1(s) =
  .

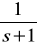
Wyznaczono:

• 
  ,

• 
  

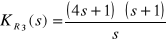
• Charakterystyka Bodego transmitancji regulatora:

• Charakterystyka Bodego transmitancji układu zamkniętego i obiektu:

• Charakterystyka Bodego transmitancji układu otwartego:

• Charakterystyka Nyquista transmitancji regulatora:

• Charakterystyka Nyquista transmitancji układu otwartego:

• Charakterystyka Nyquista transmitancji obiektu i układu zamkniętego:

1. Wnioski:
   

W ćwiczeniu mogliśmy zapoznać się z metodami wyznaczania charakterystyk częstotliwościowych układów regulacji, oraz ich bloków składowych.

W ćwiczeniu pierwszym zauważyliśmy, że po włączeniu regulatora, który miał zmniejszyć stałą czasową (polepszyć dynamikę) nastąpiło poszerzenie pasma. Charakterystyka regulatora przypomina charakterystykę regulatora typu PI, natomiast transmitancja układu otwartego stanowi idealny integrator, co potwierdzają zamieszczone przebiegi transmitancji.

W ćwiczeniu 2 zauważyć można wpływ regulatora. Nastąpiło zmniejszenie tłumienia - wzrósł rząd transmitancji.

Na podstawie charakterystyk Nyquista możemy określić rzędy transmitancji. W ćwiczeniu 1 półokrąg potwierdzający układ pierwszego rzędu, natomiast w pozostałych ćwiczeniach układy drugiego i trzeciego rzędu (kształt spiralny). Analizując przebieg otrzymanych charakterystyk, oraz wzorów naszych transmitancji stwierdzamy, że wszystkie badane przez nas układy są stabilne. Wyraźnie widać, że charakterystyki Nyquista nie przechodzą przez punkt -1, j0 oraz nie zataczają one tego punktu z lewej strony.

Laboratorium automatyki i sterowania

Strona 17 z 17

Schemat układu otwartej regulacji:

K_Z1(jω)

K_O(jω)

K_Z2(jω)

K_OTW(jω)

K_O2a(jω)

K_Z2a(jω)

K_Z2a(jω)

K_o2a(jω)

K_Z2b(jω)

K_o2b(jω)

K_Z3(jω)

K_O3(jω)

K_O3(jω)

K_Z3(jω)

---