Laboratorium Podstaw Automatyki
MODELOWANIE CIĄGŁYCH I DYSKRETNYCH UKŁADÓW
REGULACJI
Badania w dziedzinie czasu
1. Wprowadzenie
Badania symulacyjne stanowią istotny element w procesie projektowania układów
sterowania. Przeprowadza się je głównie w przypadkach, gdy ze względu na występujące w
układzie nieliniowości lub jego złożoną strukturę, rozwiązania analityczne nie istnieją albo są
zbyt skomplikowane. Przykładowo w przypadku nieciągłych (impulsowych) układów regulacji
metoda symulacji pozwala w sposób łatwiejszy określić wpływ odstępu próbkowania na
działanie układu, niż żmudna analiz dużej liczby transmitancji nieciągłych. Przed
przystąpieniem do symulacji układów skomplikowanych, których działania nie jesteśmy w
stanie przewidzieć, celowe jest przeprowadzenie symulacji układów uproszczonych (np.
zlinearyzowanych) w celu zorientowania się co do wpływu poszczególnych parametrów na
wyniki symulacji. Wówczas dobór sensownych zakresów zmian parametrów jest łatwiejszy.
W
ćwiczeniu tym elementy i układy regulacji badane są metodą modelowania
numerycznego (symulacji numerycznej). Wykorzystywany jest program MatLab wraz z
pakietem Simulink zawierającym zestaw funkcji stanowiących modele dynamiczne
podstawowych elementów: źródeł sygnałów, elementów liniowych ciągłych i dyskretnych,
elementów nieliniowych i różnych elementów pomocniczych. Simulink wykorzystuje graficzne
środowisko WINDOWS, umożliwiając łatwe opisywanie modelowanych układów przez
tworzenie ich schematów blokowych. W instrukcji podano podstawowe informacje na temat
wykorzystywanych programów. Szerszy opis programu Matlab i pakietu Simulink można
znaleźć w literaturze [1, 2, 3].
W ramach przygotowania do ćwiczenia należy zapoznać się z podstawowymi zagadnieniami
dotyczącymi metod numerycznych (np. [4, 5, 6]).
2. Opis programu MatLab i biblioteki Simulink
Matlab jest językiem programowania wysokiego poziomu zawierającym kilkaset
standardowych funkcji przeznaczonych do opisu i rozwiązywania specjalistycznych zagadnień z
różnych działów matematyki. Możliwości Matlaba poszerzają tzw. przyborniki, które są
specjalizowanymi pakietami funkcji przeznaczonych do rozwiązywania zagadnień z różnych
dziedzin, np. teorii regulacji, identyfikacji, analizy sygnałów, optymalizacji, przetwarzania
obrazów, modelowania sieci neuronowych itp.
Po uruchomieniu Matlaba pojawia się znak zachęty (prompt) ">>" oznaczający gotowość
do pracy. Znak ten otwiera linię poleceń. W kolejnych liniach wpisuje się nazwy instrukcji
języka Matlab, tworząc program. Poniweaż program Matlab pracuje jako interpreter, to możliwa
jest również praca interaktywna, tj. natychmiastowe wykonywanie obliczeń wg wprowadzonych
instrukcji. Możliwe jest też wpisanie nazwy funkcji lub wcześniej przygotowanego programu.
Opis wybranego elementu języka Matlab można uzyskać przez wpisanie polecenia help
nazwa elementu.
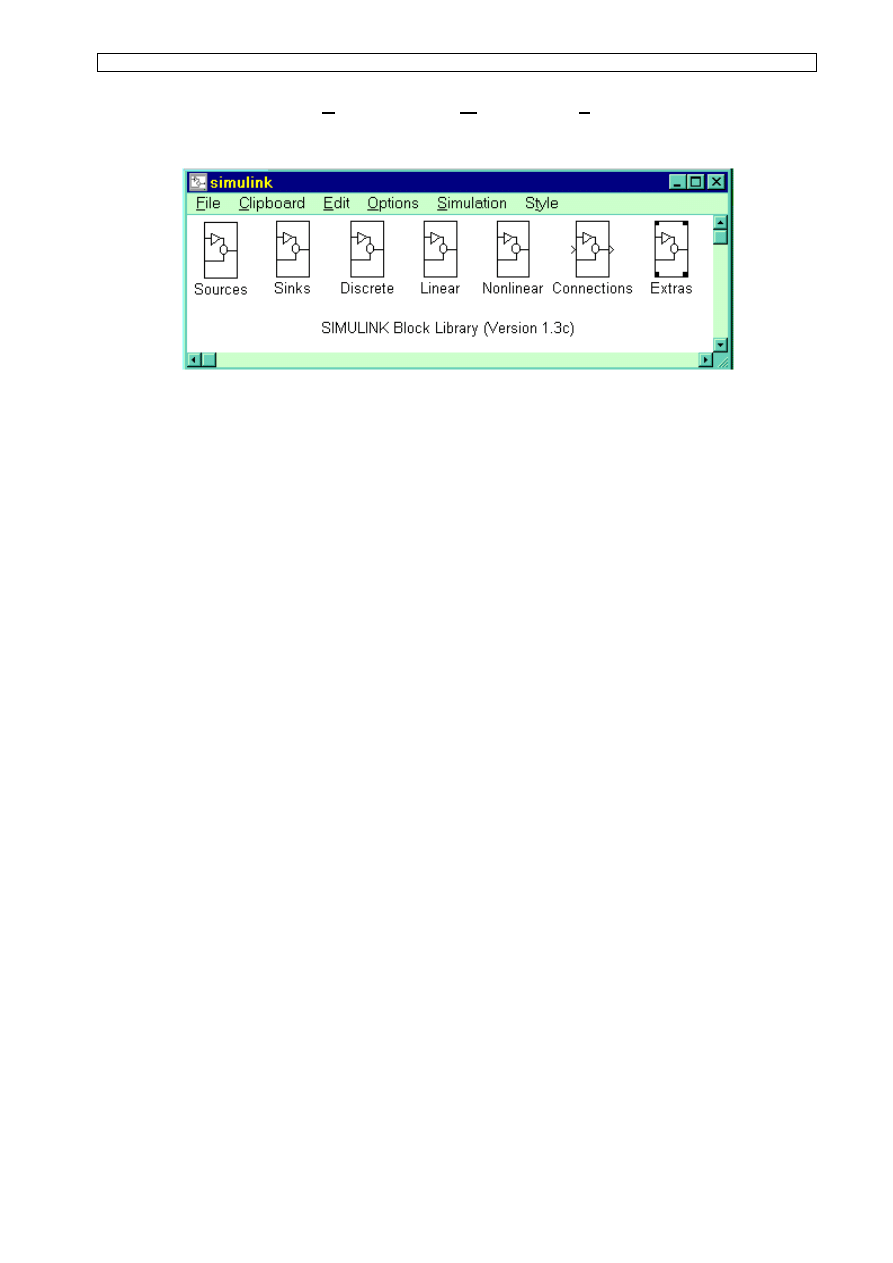
Otwarcie okna pakietu Simulink (rys.1) możliwe jest na dwa sposoby:
•
Przez wpisanie polecenia Simulink w linii poleceń. Jest to okno biblioteczne, ponieważ
zawiera zestaw symboli graficznych grup elementów, umożliwiających budowanie
schematu blokowego modelowanego układu.
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 2 -
•
Przez wybranie opcji New, a następnie Model z menu File. W tym przypadku nie są
wyświetlane ikony grup elementów, możliwe jest natomiast wczytanie pliku z uprzednio
stworzonym modelem.
Rys. 1. Okno pakietu Simulink z grupami elementów
W oknie Simulinka dostępne są następujące grupy elementów:
•
Sources
elementy
generujące różne sygnały pobudzające badane układy,
•
Sinks
elementy "odbierające" i wizualizujące sygnały,
•
Discrete
elementy do symulacji układów dyskretnych,
•
Linear
elementy do symulacji układów liniowych ciągłych,
•
Nonlinear
elementy do symulacji układów nieliniowych,
•
Conections
elementy pomocnicze, służące do wykonywania połączeń między
elementami
modelowanego
układu,
•
Extras
elementy dodatkowe
Każdy grupa elementów może być rozwijana przez dwukrotne kliknięcie przyciskiem myszy -
uzyskuje się wówczas dostęp do poszczególnych elementów. Podobnie, przez wskazanie i
dwukrotne kliknięcie, uzyskuje się dostęp do parametrów każdego z elementów, zarówno w
ramach poszczegółnych bibliotek, jak i w ramach tworzonego schematu blokowego badanego
układu.
W podanym niżej skrótowym opisie elementy najczęściej wykorzystywane w ćwiczeniu
wyróżniono przez pogrubienie ich nazwy.
Grupa Sources:
Clock
- generator czasu, podaje czas bieżący w trakcie symulacji, uniezależnia skalę czasu od
szybkości komputera
Digital Clock
- j. w. lecz zdyskretyzowany z zadanym odstępem próbkowania
Repeating Sequence
- sekwencja wartości definiowana przez użytkownika
Signal Generator
- generator funkcyjny (sygnał sinusoidalny, piłowy, prostokątny lub
losowy)
Constant
- wartość stała w czasie
Pulse Generator
- generator sygnału impulsowego o zadanych parametrach
Sine Wave
- generator sygnału sinusoidalnego
Step Input
- generator sygnału skokowego o deklarowanych wartościach początkowej i
końcowej oraz czasie skokowej zmiany wartości
From File
- wartości odczytywane z pliku
From Workspace
- odczyt danych z przestrzeni roboczej (pamięci danych) Matlaba
Crip Signal
- sygnał sinusoidalny o częstotliwości wzrastającej liniowo
Random Number
- sygnał pseudoprzypadkowy generowany w każdym kroku całkowania
numerycznego
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 3 -
Band-Limited White Noise
– j.w., ale nowa wartość generowana co zadany odstęp
próbkowania; zastosowanie zamiast Random Number pozwala przyspieszyć czas
obliczenia
Grupa Sink:
Scope
- wykreśla przebieg sygnału anaolgicznie do oscyloskopu
Graph
- wykres czasowy wartości sygnału, przy stałych zakresach czasu i wartości sygnału,
deklaruje się zakresy wartości na osiach, oraz typ i kolor poszczególnych linii wykresu
Auto-scale Graph
- j.w. lecz skala dopasowuje się automatycznie do wartości,
dodatkowo deklaruje się maksymalną licznę punktów, które obejmuje wykres
XY-Graph
- wykres sygnału Y w funkcji sygnału X
To Workspace
- przekazuje dane do przestrzeni roboczej Matlaba
To File
- zapisuje dane w pliku
Stop Simulation
- zatrzymanie symulacji, gdy na wyjściu pojawi się sygnał różny od zera
Hit Crossing
- zmniejsza krok całkowania (zwiększa dokładność obliczeń) po
przekroczeniu zadanej wartości sygnału
Grupa Discrete:
Uwaga: okres próbkowania może być definiowany oddzielnie dla każdego elementu.
Unit Delay
- opóźnienie sygnału o jeden okres próbkowania, deklaruje się okres
próbkowania i wartość początkową
Discret Zero-Pole
- transmitancja dyskretna definiowana przez podanie zer, biegunów
i współczynnika wzmocnienia.
Filter
- transmitancja dyskretna definiowana w postaci funkcji wymiernej zmiennej z
-1
Discrete Transfer Fn
- transmitancja definiowana w postaci funkcji wymiernej
zmiennej z
Discrete State-Space
- element opisany za pomocą równań stanu
Zero Order-Hold
- ekstrapolator zerowego rzędu dla danego czasu próbkowania
First Order-Hold
- ekstrapolator pierwszego rzędu dla danego czasu próbkowania
Discrete Time Integrator
- dyskretny element całkujący, deklaruje się okres
próbkowania i wartość początkową
Grupa Linear
Sum
– sumator wartości z poszczególnych wejść, deklaruje się znaki dla poszczególnych
wejść
Inner Product
- element mnożący dwa sygnały wejściowe
Integrator
- element całkujący z deklarowanym warunkiem początkowym
Derivative
- element różniczkujący
Gain
- element proporcjonalny (wzmacniacz)
Matrix Gain
- element mnożący sygnał wektorowy przez zadaną macierz
Slider Gain
- element proporcjonalny o wzmocnieniu zadawanym graficznie (za pomocą
suwaka)
Transfer Fn
- transmitancja operatorowa K(s) w postaci funkcji wymiernej; wielomiany
licznika i mianownika definiuje się przez podanie współczynników począwszy od
współczynnika przy najwyższej potędze zmiennej s
Zero-Pole
- transmitancja definiowana przez podanie zer, biegunów i wzmocnienia
State-Space
- element opisany równaniami stanu
Grupa Nonlinear
Sign
- realizuje finkcję sign (określa znak) dla sygnału wejściowego
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 4 -
Ralay
- symuluje przekaźnik dwupołożeniowy z histerezą, deklaryje się warunki załączenia i
wyłączeia oraz wartości na wyjściu w stania załączenia i wyłączenia
Backlash
- modeluje histerezę
Saturation
- wzmacniacz bezinercyjny z nasyceniem, deklaryje się górną i dolną wartość
w stanie nasycenia
Quantizer
- symuluje kwantowanie z zadanym krokiem
Dead Zone
- symuluje strefę martwą (przedział nieczułóści)
Rate Limiter
- ogranicza szybkość zmian sygnału
Product
- element mnożący sygnały wejściowe
Abs
- określa wartość bezwzględną sygnału
Look_Up Table
- wyznacza wartości funkcji odcinkowo-liniowej o węzłach zadanych w
postaci tablicy
2-D
Look-Up Table - analogicznie j.w. lecz dla dwóch sygnałów (tablica
dwuwymiarowa)
Relational Operator
- porównanie sygnałów wejściowych wg zadeklarowanego
operatora relacji
Logical Operator
- j.w. lecz deklarowana jest relacja logiczna
Combinatorial Logic
- realizuje funkcję logiczną opisaną tablicą prawdy
Fcn
- przetwarza sygnał wejściowy wg zadeklarowanej funkcji typu y=f(x)
S-Function
- przetwarza sygnał wg tzw. funkcji systemowej, tj. dowolnej funkcji
zdefiniowana wcześniej w języku Matlaba
MATLAB Function
- przetwarza sygnał wg funkcji standardowej Matlaba
Reset Integrator
- element całkujący z możliwością restartu, tj. ponownego
rozpoczęcia całkowania od wartości podanej na drugie wejście (wartość początkowa), w
chwili gdy wartość na trzecim wejściu staje się niezerowa
Memory
- element pamięci sygnału, wprowadza opóźnienie o jeden krok całkowania
Transport Delay
- opóźnienie transportowe (przesunięcie sygnału w czasie), deklaruje
się czas opóźnienia
Variable Transport Delay
- sterowane opóźnienie transportowe
Limited Integrator
- element całkujący z ograniczeniem, deklaruje się dolną i górną
wartość ograniczenia oraz wartość początkową
Grupa Connections:
Inport
- wejście do symulowanego systemu, jeżeli jest on podsystemem
Outport
- wyjście z symulowanego systemu, jeżeli jest on podsystemem
Mux
- multiplekser łączący kilka sygnałów skalarnych w jeden sygnał wektorowy,
wykorzystywany dla zobrazowania kilku przebiegów na jednym wykresie Auto-scale
Graph
Demux
- demultiplekser rozdzielający sygnał wektorowy na sygnały skalarne
Grupa Extras:
Simulink Demos
- przykłady systemów do symilacji w simulinku
Most commonly used blocks
- zawiera najczęściej używane elementy z różnych grup.
Grupę tę można bezpośrednio otworzyć z linii poleceń Matlaba poleceniem blicklib.
Convertion
- elementy pozwalające dokonać konwersji układu współrzędnych
Flip-Flops
- elementy symulujące przerzutniki D, SR itp.
PID Controllers
- elementy symulujące regulatory PID
Analyzers
- elementy do przetwarzania i analizy sygnałów
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 5 -
W górnej części okna Simulink umieszczona jest linia zleceń. Poza typowymi w systemie
WINDOWS grupami zleceń (File, Edit) istnieje grupa zleceń do określania parametrów
symulacji: Simulation. Poszczególne zlecenia są następujące:
Start - uruchumienie symulacji / Stop - przerwanie symulacji
Pause - zatrzymanie symulacji
Restart - wznowienie symulacji
Parameters - wybór rodzaju algortymu całkowania numerycznego i parametrów:
Start Time - czas rozpoczęcia symulacji
Stop Time - czas zakończenia obliczeń
Min Step Size, Max Step Size - minimalny i maksymalny krok czasowy całkowania
numerycznego
Tolerance - dopuszczalny błąd całkowania
Return Variables - nazwa zmiennej pojawiającej się w przestrzeni roboczej Matlaba po
zakończeniu symulacji
Przeprowadzenie badani asymulacujnego wymaga stworzenia schematu blokowego
stanowiącego model badanego układu. Konstruowanie nowego modelu polega na:
•
Otwarciu nowego okna (zlecenie File | New)
•
Przenoszeniu do tego okna ikon reprezentujących potrzebne elementy wybrane z
odpowiednich grup elementów (uprzednio otwartych podwójnym kliknięciem)
•
Połączeniu wejść i wyjść tych elementów w odpowiednią strukturę - przez ciącnięcie linii od
wyjść do wejść przy wciśniętym lewym przycisku myszy
•
Nadaniu parametrom elementów układu pożądanych wartości - przez podwójne kliknięcie na
ikonie elementu rozwija się okno jego parametrów
Uruchomienie symulacji odbywa się poleceniem Simulation | Start.
3. Modelowanie wybranych elementów i układów
W ramach ćwiczenia należy przeprowadzić symulacyjne badanie elementów i układów
wskazanych przez prowadzącego. Poniżej przedstawiono przykładowe zagadnienia.
3.1. Układy ciągłe
I. Modelowanie na podsatwie równań różniczkowych.
Podstawą do modelowania układu jest jego opis w postaci równania różniczkowego. Na
jego podstawie tworzony jest schemat strukturalny złożony z podstawowych elementów
realizujących operacje statyczne (sumowanie i wzmocnienie proporcjonalne) oraz dynamiczne
(całkowanie i różniczkowanie) a także penne operacje nieliniowe w przypadku modelowania
układów nieliniowych.
Jako przykład wykorzystany jest element opisany równaniem różniczkowym o postaci:
)
t
(
x
b
)
t
(
y
dt
)
t
(
dy
a
dt
)
t
(
dy
a
1
2
2
2
=
+
+
Przyjmując oznaczenia: y
1
=y i y
2
=y' równanie (1) można zapisać w postaci układu równań:
y
1
' = y
2
⇔ y
1
=
∫ y
2
dt
y
2
' = b/a
2
x - (a
1
/a
2
)
y
2
- (a
0
/a
2
)
y
1
Układ taki można zamodelować wykorzystując elementy całkujące i proporcjonalne.
Odpowiedni schemat pokazano na rys. 2
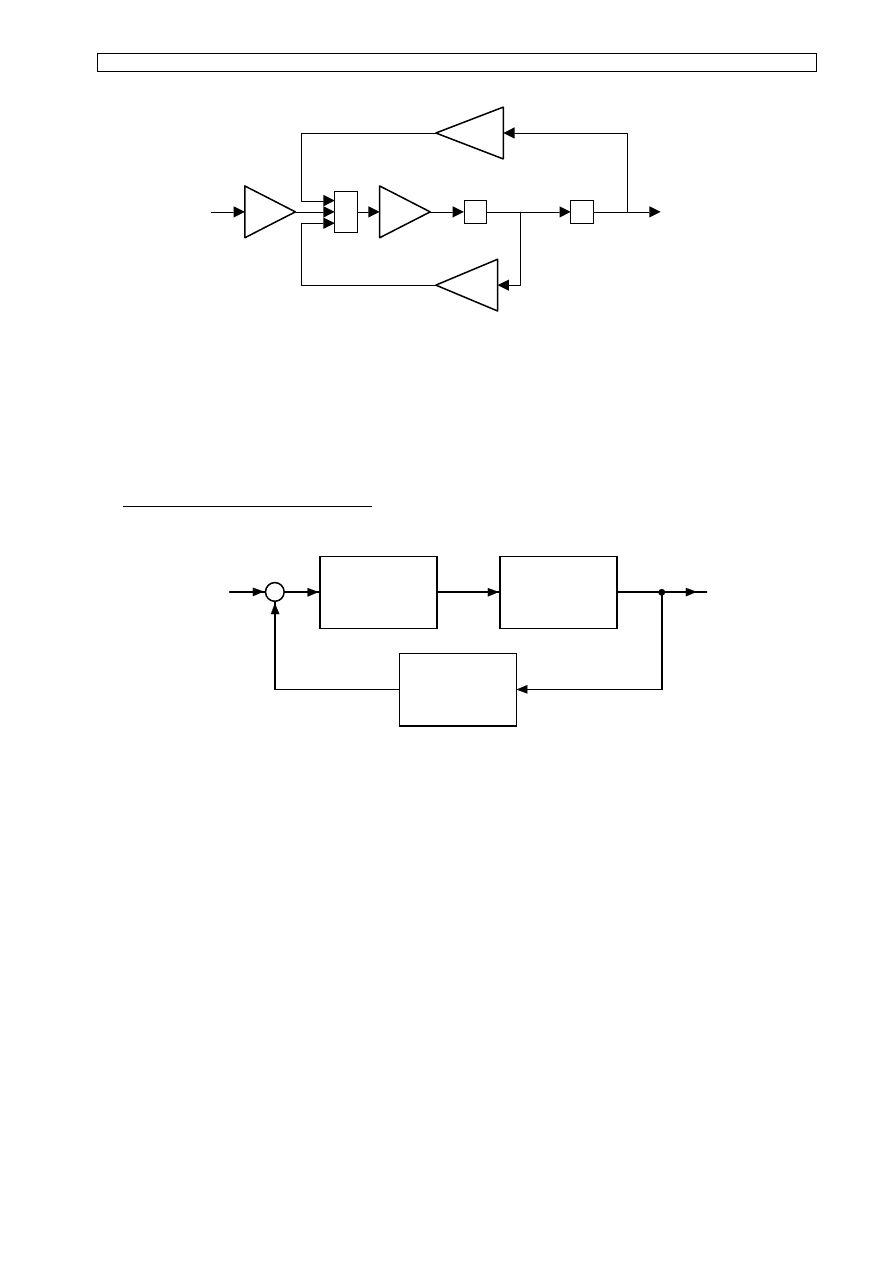
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 6 -
_
+
b
a1
1/s
1/s
1/a2
a0
y (t)=y(t)
y (t)
y (t)
x(t)
całkowanie
2
2
1
'
wzmocnienie
sumator
_
Rys. 2. Struktura modelu elementu opisanego równaniem drugiego rzędu.
W
ramach
ćwiczenia należy wyznaczyć analogiczny schemat modelu układu opisanego
podanym przez prowadzącego równaniem różniczkowym lub transmitancją oraz wyzanaczyć
przebiegi odpowiedzi tego układu na zadane sygnały wejściowe.
II. Modelowanie układów złożonych
Typowa struktura zamkniętego układu regulacji pokazana jest na rysunku 3.
+
-
Yz
Yp
Y
U
ε
Kr
Regulator
Ko
Obiekt
Kp
Układ
pomiarowy
Rys. 3. Zamknięty układ regulacji
Należy przeprowadzić badania układu przyjmując różne założenia:
a) Dana jest transmitancja obiektu Ko = 1/(10s+1) oraz układu pomiarowego Kp = 1. Należy
zaprojektować regulator (wyznaczyć jego transmitancję), tak, aby czas odpowiedzi na
skokową zmianę wartości zadanej dla całego układu był mniejszy
α krotnie od czsu
odpowiedzi obiektu, a wzmocnienie nie uległo zmianie. Przeprowadzić symulacje
przyjmując różne wartości współczynnika
α. Rejestrować następujące sygnały: wejściowy,
wyjściowy układu i dla porównania wyjściowy dla analogicznego obiektu w układzie
otwartym oraz sygnał na wyjściu zaprojektowanego regulatora.
b) Zbadać zachowanie się układu w sytuacji, gdy rzeczywista transmitancja obiektu jet różna od
przyjętej do projektowania regulatora. Taka sytuacja może mieć miejsce jeżeli identyfikacja
rzeczywistego obiektu nie jest przeprowadzona wystarczająco dokładnie.
Przyjąć następujące transmitancje obiektów:
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 7 -
( ) ( )( )
( )
(
)
(
)
1
095
0
1
0
1
5
1
1
1
4
1
2
+
+
+
=
+
+
=
s
.
s
,
s
s
K
s
s
s
K
b
a
Porównać wykresy odpowiedzi czasowych obiektu z punktu a) i podanych wyżej.
3.2. Układy impulsowe
I. Elementy: całkujący, różniczkujący, inercyjny 1-rzędu i 2-rzędu
Wzorując się na podanym niżej przykładzie należy:
a) wychodząc z równania różniczkowego odpowiedniego elementu ciągłego wyprowadzić
równanie w postaci różnicowej, a następnie przekształcić do postaci rekurencyjnej
b) skonstruować model i przeprowadzić badanie symulacyjne, zakładając różne okresy
próbkowania
Przykład: Równanie różniczkowe opisujące ciągły element inercyjny pierwszego rzędu ma
postać
( ) ( ) ( )
t
kx
t
y
dt
t
dy
T
=
+
Przybliżając pochodną ilorazem różnicowym oraz przyjmując oznaczenia:
t
k
=k
Δ
t,gdzie k oznacza numer bieżącej chwili czasowej, a
Δ
t jest okresem
impulsowania, można zapisać:
( ) ( ) ( ) (
k
k
k
k
t
x
k
t
y
t
t
y
t
y
T
1
1
=
+
Δ
)
−
−
−
a stąd po przekształceniach uzyskuje się równanie rekurencyjne:
( )
( ) ( )
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
Δ
−
−
Δ
==
−
t
T
t
y
t
x
k
T
t
t
y
k
k
k
1
1
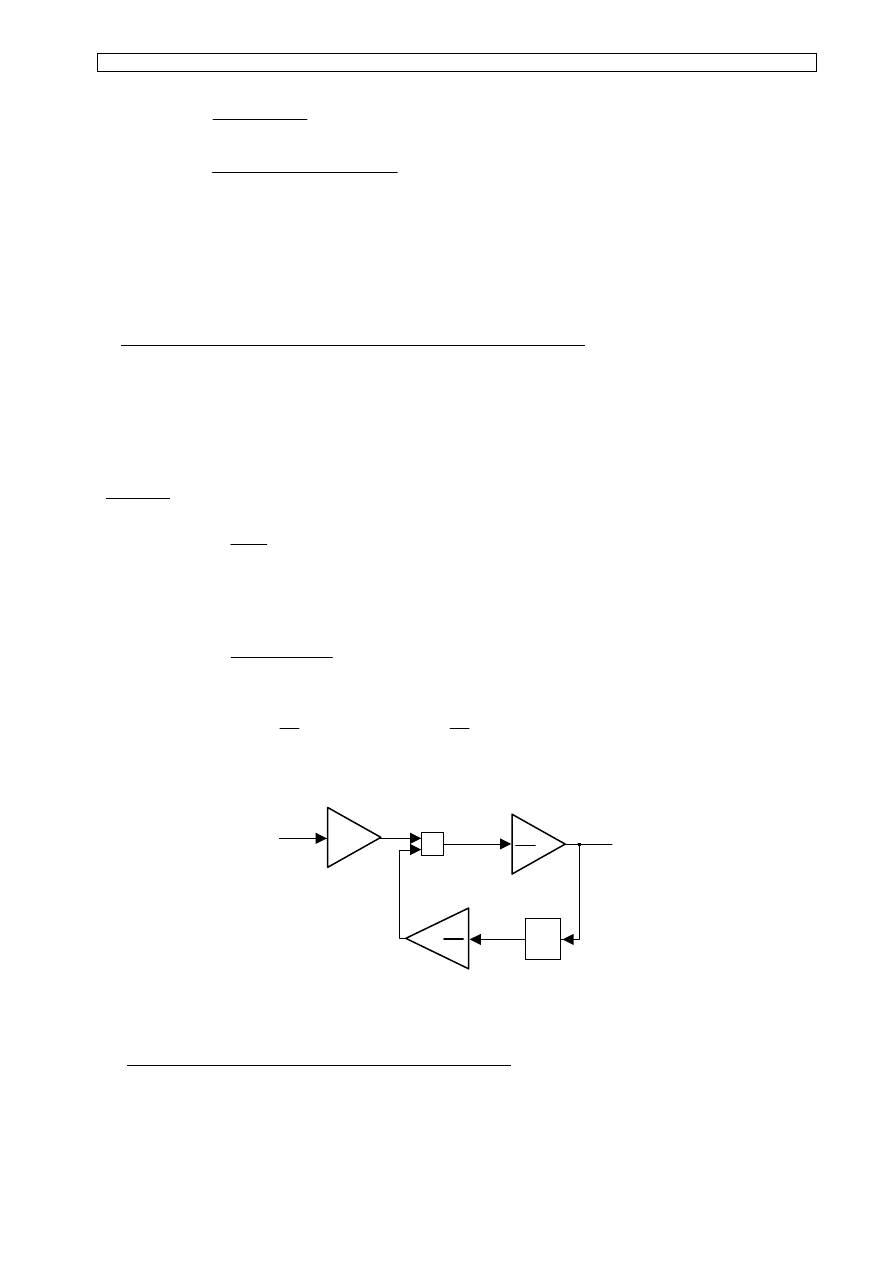
Równanie takie można zamodelować układem przedstawionym na rysunku 4.
+
_
1/z
k
t
Δ
T
1-
t
Δ
T
y t
( )
k
x t
( )
k
y t
( )
k-1
sumator
wzmocnienie
opóźnienie
Rys.4. Schemat strukturalny modelu impulsowego elementu
inercyjnego pierwszego rzędu
II. Układ regulacji (wg rys. 3) z regulatorem nieciągłym
a) Zamodelować regulator dyskretny dobrany przy założeniach jak w pkt. 3.1.IIa
b) przeprowadzić badanie symulacyjne układu dla różnych okresów próbkowania
3.3. Układy nielinowe
Laboratorium Podstaw Automatyki
Modelowanie – dziedzina czasu
- 8 -
I. Zamknięty układ regulacji
Sprawdzić działanie układu regulacji pokazanego na rysunku 3 z regulatorem dobranym jak
w pkt. 3.1.IIa w następujących sytuacjach:
a) przy założeniu ograniczenia mocy dostarczonej do wejścia obiektu przez regulator (każdy
elemnent rzeczywisty podlega takim ograniczeniom), wstawiając na wyjściu regulatora
element Saturation z grupy Nonlinear. Założyć poziom ograniczenia mniejszy niż
przyjęty stopień skrócenia czasu odpowiedzi
α.
b) obiekt jest elementem pierwszego rzędu z opóźnieniem (element Transport Delay z
grupy Nonlinear); obliczenie przeprowadzić dla różnych wartości czasu opóźnienia.
4. Pytania kontrolne.
1. Co wyróżnia elementy dynamiczne?
2. Wymień podstawowe typy elementów dynamicznych idealnych.
3. Jakie znasz sposoby opisu matematycznego tych elementów?
4. Jakie parametry charakteryzują dynamikę elementów i układów?
5. Narysuj trzy podstawowe struktury połączeń elementów w układach regulacji?
6. Jakie elementy nazywa się ciągłymi, a jakie nieciągłymi (impulsowymi)?
7. Czy jest możliwe włączenie w jednym układzie elementów ciągłych i impulsowych? W
jaki sposób?
8. Czy współczynniki równań opisujących elementy dyskretne zależą od okresu
próbkowania? Dlaczego?
9. Omów analityczne sposoby wyznaczania odpowiedzi układów dynamicznych?
10. Jakie miary mogą służyć do oceny jakości regulacji?
11. Jaki jest sens numerycznego modelowania ukadów dynamicznych?
12. Omów zagadnienie nieliniowości w układach sterowania.
13. Wskaż różnice pomiędzy elementami idealnymi (opisanymi modelema uproszczonym), a
rzeczywistymi (realizowalnymi fizycznie). Podaj przykłady.
Literatura:
[1] Klamka J., Ogonowski Z.: Teoria systemów liniowych. Skrypt Pol. Śląskiej, Gliwice,
1996.
[2] Brzózka J.: Ćwiczenia z automatyki w Matlabie i Simulinku. Wyd. Mikom, Warszawa,
1997
[3] Osowski S.: Modelowanie układów dynamicznych z zastosowaniem języla SIMULINK.
Oficyna wydawnicza Polit. Warszawskiej, 1999
[4] Krupka. J., Morawski R.Z., Opalski L.J.: Wstęp do metod numerycznych., Oficyna
wydawnicza Polit. Warszawskiej, 1999
[5] Fortuna Z., Macukow B., Wąsowski J.: Metody numeryczme. WNT, 1982
[6] Bogucka S. (red.):Metody numeryczne w technice. skrypt Polit. Śląskej, nr 418, Gliwice,
1973
(HUk), plik: SYM_T_27-01.DOC
Document Outline