RUCH

W FIZYCE:

Ruchem nazywamy zmianę położenia ciała odbywającą się w czasie postrzeganą przez obserwatora zwanego układem odniesienia. Podstawowe prawa rządzące ruchem sformułował Izaak Newton. Obecnie ruch ciał fizycznych opisują trzy teorie:

• Mechanika klasyczna (opisująca ruch obiektów niezbyt małych i poruszających się niezbyt szybko);

• Teoria względności

• Szczególna teoria względności (opisująca ruch ciał o prędkościach porównywalnych z prędkością światła, ale nie uwzględniająca grawitacji);

• Ogólna teoria względności uwzględniająca grawitację

• Mechanika kwantowa (opisująca zachowanie się obiektów małych takich jak atomy, cząstki subatomowe)

W FILOZOFII:

Ruchem nazywamy zmianę bądź miejsca w przestrzeni, bądź ilościową, jakościową, bądź istotną lub powierzchniową, której podlega wszystko, co jest skończone. Problematyka ruchu została poruszona już w starożytności:

• Heraklit - podkreślał, że zasadniczą cechą rzeczywistości jest dynamizm. Zwrócił uwagę na zmienność, na nieustanną ruchliwość (wszystko, co istnieje porusza się, zmienia, przeobraża). Stąd: panta rhei - „wszystko płynie i nic nie trwa”, a także „nie wchodzi się dwa razy do tej samej rzeki”. Dla niego stawanie się jest nieustanną walką, ścieraniem się przeciwieństw.

• Parmienides - teza przeciwna do myśli Heraklita tzw. parmenidejska zasada prawdy: „byt jest i nie może nie być; nie-byt nie jest i nie może w żaden sposób być”. Byt jest jedyną rzeczą, a ruchu nie ma. W związku z tym byt ma takie własności, że jest niezmienny, absolutny i nie podlega żadnej zmianie.

• Zenon z Elei - najwybitniejszy uczeń Parmenidesa, który będzie wskazywał, że nie ma czegoś takiego, jak zmiana, że ruch jest tylko pewnym złudzeniem. Stworzył cztery argumenty przeciwko ruchowi (paradoksy):

1. Dychotomia (aby przebyć drogę z jednego punktu do drugiego najpierw trzeba przebyć połowę tej drogi, ale za nim tam dotrzemy to musimy przebyć połowę tej drogi itd. i tak w nieskończoność, z czego wynika, że ruch jest złudzeniem).

2. Achilles (najszybszy biegacz nigdy nie dogoni najwolniejszego (Achilles nie dogoni żółwia), gdyż zanim Achilles dotrze do punktu, z którego żółw wyszedł też zdąży posunąć się do przodu. Takie rozumowanie prowadzi się w nieskończoność).

3. Strzały (rzecz, która znajduje się w ruchu w bardzo krótkim przedziale czasu jest w spoczynku, zaś czas jest sumą chwil, a zatem strzała nie może się poruszać).

4. Stadion (podkreśla się względność ruchy - prędkość ruchu mierzona względem jakiegoś układu odniesienia; zawodnik, który biegnie ma inną prędkość względem drugiego zawodnika i inną względem ludzi siedzących na trybunach).

Arystoteles - stwarza serie pojęć takich, jak potencja i aktualność. Ruch, zmianę i czas związał z bytującym konkretem i uczynił przedmiotem filozoficznego badania. Dla niego ruch to generalnie zmiana (w organizmie, w przyrodzie, itd.). Od jego czasów odróżnia się sytuację, w której przyczyna ruchu znajduje się w poruszanej rzeczy, stanowiąc jej naturę, jej wewnętrzny napęd, od takiej, w której przyczyna jest wobec niej zewnętrzna.

Platon - sprowadza on wszelkie zmiany do ruchu przestrzennego mającego przyczyny mechanicystyczne.

PARADOKS ACHILLESA

Bezpośrednich tekstów Zenona z Elei nie posiadamy, ale jest zapis jego paradoksów w „Fizyce” Arystotelesa: „Drugi argument tzw. Achilles, sprowadza się do tego, że w wyścigu najszybszy biegacz nie może nigdy prześcignąć najpowolniejszego. Tym najszybszym jest Achilles, tym najpowolniejszym żółw - stąd nazwa. Ścigający musi najpierw osiągnąć punkt, z którego ścigany już wyruszył (każdy punkt na drodze Achillesa odpowiada punktowi na drodze żółwia, a więc punktów jest tyle samo na drodze Achillesa, co na drodze żółwia), tak że powolniejszy ma zawsze pewne wyprzedzenie.” Strasznie trudno zbić ten argument, ponieważ jak patrzymy na doświadczenie to oczywistością jest, iż Achilles dogoni żółwia, ale jeśli przyjmiemy sposób rozumowania Zenona to nie jest już takie proste. Jeżeli przyjmiemy, że oni wystartowali z dwóch punktów różniących się o jakiś odstęp to, jeśli Achilles dotarł do tego miejsca gdzie był żółw to ten przesunął się do następnego i tak w nieskończoność. Mamy nieskończoną liczbę odcinków drogi, którą Achilles musi pokonać i nieskończoną ilość chwil czasowych. Rozumowanie Zenona ma taki przebieg, że tego nie można zrobić w skończonym czasie, więc go nie dogoni.

PARADOKS STRZAŁY

„Trzeci argument powiada, że mianowicie wypuszczona strzała stoi w miejscu. Wynika to z supozycji, że czas składa się z szeregu „teraz”. Jeżeli się tego nie założy, wniosek nie wyniknie. (…) Zenon twierdzi mianowicie, że skoro wszystko albo zawsze znajduje się w staniu spoczynku, albo w ruchu, i że jest w spoczynku, gdy zajmuje równą sobie przestrzeń, a to, co jest w ruchu, znajduje się zawsze w jakimś „teraz”, wobec tego strzała wypuszczona z łuku stoi w miejscu”. Polega on ta ty, że Zenon rozumuje w taki sposób, iż strzała niby się porusza, a tak naprawdę ciągle jest nieruchomo w miejscu. Jeśli weźmiemy strzałę w jakimś dowolnym momencie (t₁) to strzała niewątpliwie jest wtedy bezruchu (zajmuje jakieś położenie i nie rusza się). Jeśli weźmiemy w innej chwili (t₂) to sytuacja jest podobna. Ruch byłby nieskończoną ilością punktów chwil, w których strzała się nie rusza, więc ruchu nie ma. Rozumowanie pokazuje, że ruch jest czymś iluzorycznym.

Ks. prof. Dr hab. Michał Heller w książce „Uchwycić przemijanie” napisze tak: „W paradoksach myśliciela z Elei zawiązał się wielki problem ruchu”. Po takim długim czasie, jaki minął od sformułowania paradoksów my od strony matematycznie je rozumiemy (potrafimy zmatematyzować rozumowanie Zenona i pokazać, że używając pojęcia granicy i szeregu wszystko się zgadza). Czy to znaczy, że rozwiązaliśmy ten paradoks? Część filozofów powie, że nie, bo mimo precyzyjnej analizy matematycznej paradoks w jakiś sposób ciągle pozostaje paradoksem. Heller z kolei uważa, że poradziliśmy sobie z paradoksem w momencie, kiedy nauczyliśmy się właściwie używać pojęcia nieskończoności za pomocą pojęć granica szeregu czy pochodna funkcji. Arystoteles w swojej „Fizyce” napisał, że dużo utrapienia ten paradoks sprawia ludziom, którzy nad nim myślą.

Dziś w perspektywie fizyki nastąpiło pewne „odchudzenie” pojęcia ruchu, ponieważ kiedyś ono opisywało jakąkolwiek zmianę, która w świecie się dokonywała, zaś teraz fizyka w swoim obrębie zawęża jego znaczenie do ruchu przedmiotów materialnych w przestrzeni. To będzie rozwijane jako kinematyka (dział fizyki).

Podstawowym aksjomatem współczesnego przyrodoznawstwa jest to, iż posługuje się ono językiem matematyki, więc jakikolwiek zjawisko czy fenomen jest w tych kategoriach opisywany.

Fizyk do modelowania przestrzeni przyjmuje trójwymiarową przestrzeń euklidesową. Na niej obserwujemy ruch, który jest zmianą położenia w tej przestrzeni podczas upływającego czasu, więc ruch jest szczególną koncepcją, która łączy chwile czasowe z punktami w przestrzeni. Pojawiają się pytania, jaki będzie matematyczny model czasu i jak będzie wyglądać opis ruchu?

MATEMATYCZNY MODEL CZASU

1. Jest nasze bogate doświadczenie czasowości, które zarazem jest trudne do wykorzystania, aby opisać ruch. Np. doświadczenie fenomenologiczne w modelach nie ma swojego miejsca. Natomiast musimy uwzględniać porządek chwil czasowych.

Ex1. Są okresy w naszym życiu kiedy człowiekowi jest dobrze i wtedy on zapomina, że czas płynie. Z kolei gdy nas coś boli to czas nam się dłuży. Upływ czasu różnie obieramy w zależności od naszych doświadczeń i nastroju. Ten rodzaj opisu czasu jest dla mnie ważny, ale dla opisu zjawisk przyrodniczych nie ma żadnego znaczenia.

Ex2. Z kolei pewne doświadczenia z naszego życia mają znaczenie dla modelu czasowego, np. rozróżnienie chwili wcześniejszej i późniejszej, wcześniej i potem. Pewien porządek chwil, że któraś chwila jest wcześniejsza bądź późniejsza od innej.

2. Istnieje możliwość mierzenia odstępu między chwilami, więc model musi posiadać jakąś własność metryczną, która będzie oddawała jednostajny (równomierny) upływ czasu.

Ex1. Każdy z nas ma zegarek, dzięki któremu można powiedzieć ile czasu minęło od jednej do drugiej chwili, od początku wykładu do jego końca.

3. Doświadczenie ciągłości w upływie czasu. Nasza świadomość jest tak skonstruowana, że to chwyta, iż coś się wydarza bądź są chwile nieciągłości, kiedy tracimy przytomność. Podobnie jest z czasem. Gdy go doświadczamy to wiemy, że czasu nie można przeskoczyć, że na wszystko jest swój czas.

Te elementy muszą dać się zreprodukować w modelu matematycznym. Jaki ten model wybrać? Jest wiele, które do takiego opisu czasu nie będę pasować, bo nie oddadzą wszystkich własności:

1. Zbiór liczb naturalnych (1, 2, 3, 4, 5, …) - niewątpliwie widać, że w tym zbiorze panuje porządek, bo 2 jest większe niż 1, więc chwilom czasowym można przyporządkować te liczby i uznać, że porządek „wcześniejsze”, „późniejsze” oddaje. Podobnie łatwo wprowadzić odległości (odejmowanie od siebie liczb określając odległość między jedną chwilą a drugą). Ten model nie jest dobry, bo nie odda ciągłości upływu czasu (co jest między 1 a 2?). To jakby dziurawy model, że możemy patrzeć na świat tylko w określonych chwilach, a nie wiemy, co jest pomiędzy.

2. Zbiór liczb wymiernych (oprócz liczb naturalnych także wszystkie możliwe ułamki ). Wydaje się lepszym modelem, bo można określać bardzo malutkie odstępy między chwilami np. 0,00001s. Jednak też nie jest wystarczający, bo gdy posegregujemy wszystkie liczby wymierne to się okazuje, że gdy weźmiemy dwa dowolnie bliskie ułamki ( ¹/_{1 000 000} i ¹/_{1 000 001}) to odstęp między nimi jest malutki, ale okazuje się, że tu także występują luki np. liczby niewymierne (pierwiastka z dwóch nie da się przedstawić za pomocą ułamka). Takich liczb jest dużo, np. liczba Π,
   .

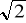
Dowód nie wprost na to, że pierwiastek z dwóch należy do zbioru liczb wymiernych.

Twierdzenie:

IW

Dowód nie wprost:

Niech:

IW


IW (q
0),
=

*q = p
2q
= p

2 (2
* 3
* 5
* ... * a
)
= (2
* 3
* 5
... * a
)

2 * 2
* 3
* 5
* ... * a
= 2
* 3

Wobec powyższego mamy, że po lewej stronie równości liczba 2 występuje w potędze nieparzystej, a po prawej stronie w potędze parzystej. Wobec jednoznaczności rozkładów na czynniki liczb identycznych otrzymaliśmy zdanie fałszywe. Mamy więc, że „
należy do zbioru liczb wymiernych” jest zdaniem fałszywym. Zatem zdanie „
należy do zbioru liczb niewymiernych” jest zdaniem prawdziwym.

c.n.d.

3. Gdy do zbioru liczb wymiernych dodamy wszystkie liczby niewymierne to dostajemy zbiór liczb rzeczywistych, który matematycznie modelujemy za pomocą prostej. Dopiero zbiór liczb rzeczywistych jest dobrym modelem, aby oddać wszystkie własności czasu (ciągłość, określenie wcześniejszego i późniejszego, jest porządek, można mierzyć odległości).

DEFINICJA FUNKCJI

Na ruch możemy popatrzeć od strony matematycznej jako na regułę przyporządkowania chwilom czasowym punktom w przestrzeni.

T - czas

a₁, a₂, a₃ - rozmaite położenia, które obiekt materialny przymnie

r - odwzorowanie

IR³ - zapis przestrzeni euklidesowej (trójwymiarowej)

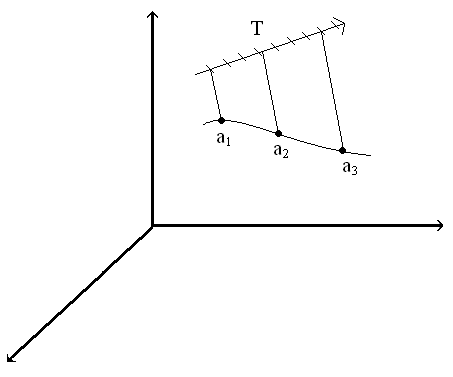
Określonym momentom

czasowym przyporządkowujemy

poszczególne położenia obiektu

materialnego (takie

przyporządkowanie nazywamy

funkcją).

r: T IR³

r(t)
IR³

Ruch będzie odwzorowaniem, który elementom osi zbioru czasu przyporządkowuje punkty w przestrzeni. Funkcja to konkretny sposób przyporządkowania tzn. każdemu elementowi zbioru t przyporządkowujemy dokładnie jeden element zbioru IR³.

RUCH JEDNOSTAJNY PROSTOLINIOWY

Jest to ruch ze stałą prędkością i w stałym kierunku, którego torem jest linia prosta, określony wzorem V = s/t

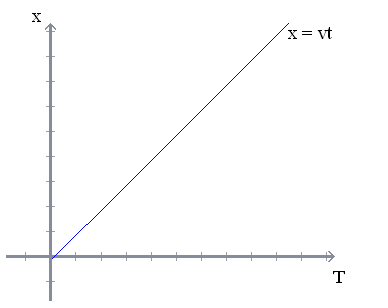
Najprostszym przykładem jest model, gdzie jedziemy na rowerze z prędkością 10km/h. Opisujemy ruch według reguły przyporządkowania za pomocą tabelki bądź ilustracji (wykresu):

T	x
1	10
2	20
3	30

T - czas

x - przebyta droga

v - współczynnik proporcjonalności

(w ruchu jedn. prost. v = constans)

x = vT

Ruch zawsze opisujemy względem czegoś, względem układu odniesienia. Układem odniesienia nazywamy dowolnie wybrany układ ciał, który w danych rozważaniach traktujemy jako nieruchomy i względem którego określamy położenie ciała. W zależności od tego gdzie umieszczę układ odniesienia względem którego będę ruch obserwował to ruch będę widział bądź też nie (gdy usiądę na dworu kolejowym to przejeżdżający pociąg porusza się względem mnie, ale dla względem pasażera siedzącego w przedziale już się nie porusza). To sprawa układu odniesienia

GRANICA CIĄGU

Bierzemy najprostszy ciąg (zbiór liczb konstruowanych według jakieś reguły) kolejnych ułamków, gdzie w mianownik wstawiamy kolejne liczby naturalne:

{a_n}:
: a_n =

{a_n} = {1,
,
,
,
, ...}

Gdy patrzymy na ten ciąg (nieskończony zbiór liczb tak zdefiniowany) to wyraźnie widać, że ma on ciekawą własność. Mianowicie wydaje się jakby te kolejne liczby były coraz bliżej 0 (jest to szczególną liczba, wokół której skupia się ten ciąg). Z jednej strony ciąg zmierza do 0, zaś z drugiej 0 do samego ciągu nie należy. W tym przypadku łatwo wskazać, że ciąg zmierza do liczby 0, ale są też takie przypadki gdzie trudno jest wskazać taką liczbę.

{b_n}:
: b_n = (1 +
)ⁿ

{b_n} = {1, 2, (1 +
)², (1 +
)², …}

Na pierwszy rzut oka nie potrafimy powiedzieć, że ten ciąg zmierza do jakieś liczby, więc trzeba podjąć badania nad jej szukaniem.

Jak wytłumaczyć i określić własność skupiania się ciągu wokół liczby? Już Zenon z Elei umiał uchwycić ten fakt, ale matematycznie to wyrazić jest o wiele trudniej. W 1821 roku pojawia się książka francuskiego matematyka, Cauchy'ego, który podaje definicję ciągu.

Definicja ciągu:

x_n = a

_{ε >0
N
n >N
n} -
< ε

Jeśli mamy dowolny ciąg x_n to jego granicą jest punkt a wtedy i tylko wtedy, gdy dla dowolnie wybranego ε istnieje taka liczba naturalna N, że dla wszystkich n większych od N, odległość między x_n i a jest mniejsza od ε.

Ta definicja uchwytuje fenomen, że od pewnego wyrazu ciągu prawie wszystkie wyrazy (za wyjątkiem skończonej ich ilości) znajdą się w dowolnie małym otoczeniu liczby a.

Liczby zagęszczają się wokół a

Liczba Eulera:
(1 +
)
= e

Ten ciąg jest zbieżny to liczby e = 2,718281828… . To jest przykład liczby, której nie można inaczej wskazać niż jak odwołując się do granicy ciągu. Znamy tylko określenie tej liczby podobnie jak jest z liczbą Π.

Cauchy wprowadzając precyzyjne pojęcie granicy nie tylko umie ściśle wyrazić, co znaczy zmierzanie do jakieś liczby, ale także daje nam pojęcie, które pozwala nam odkryć kawałek uniwersum matematycznego. Gdyby ludzie nie wpadli na pojęcie granicy ciągu to nigdy nie wiedzieliby, że istnieje liczba e. Ona daje nam nową wiedzę o świecie.

POCHODNA FUNKCJI

Granicę właściwą (jeśli istnieje) ilorazu różnicowego
dla h dążącego do zera nazywamy pochodną funkcji f w punkcie x₀ i oznaczamy symbolem f'(x₀).

f'(x₀) =

=

Geometryczna interpretacja pochodnej:

Iloraz różnicowy:

=
= tg

Zastosujemy pojęcie granicy ciągu do tego ilorazu różnicowego tzn. że konstruujemy sobie ciąg {t_n} = {Δt_1, Δt_2, Δt_{3, …}} w taki sposób, że chwile czasowe będą coraz krótsze, czyli będą zmierzały do 0. Odpowiednią do tego ciąg {x_n} = {Δx_1, Δx_2, Δx_3, …}, które również będą miały taką własność, że będą coraz mniejsze i będą zbiegać do 0. Mamy dwa ciągi (interwał przestrzenny i czasy).

Czemu będzie równa granica tak skonstruowanych ilorazów różnicowych?

Arystoteles, Fizyka, Z9, 239 b 14 nn.

Arystoteles, Fizyka, Z9, 239 b 30 nn.

6

FILOZOFIA PRZYRODY - RUCH

---