9. CHARAKTERYSTYKI STAŁOPRĄDOWE

TRANZYSTORÓW BIPOLARNYCH

9.1. Model Ebersa - Molla

Tranzystor bipolarny jest przyrządem półprzewodnikowym, w którym dwa bliskie sobie złącza n-p i p-n, oddalone nie więcej niż 1 m, wpływają na siebie poprzez iniekcję i ekstrakcję nośników mniejszościowych do bazy - wspólnego obszaru środkowego. Nośniki te tworzą tzw. prąd sprzężenia (prąd elektronowy I_n w strukturze złącz n-p-n).

Model Ebersa-Molla (E-M) przedstawia tranzystor jako kombinację dwóch parametrycznych źródeł prądowych, sterowanych sąsiednimi prądami diodowymi. Są to diody z prądami dyfuzyjnymi w obszarze bazy o przeciwsobnych potencjałach dyfuzyjnych na złączu emiterowym i złączu kolektorowym w układzie o wspólnej bazie (WB) - rys.9.1. W takiej konfiguracji nie ma wzmocnienia prądowego, ale poprzez podłączenie dużej rezystancji obciążenia można uzyskać wzmocnienie napięcia i mocy.

Rys.9.1. Modele Ebersa-Molla dla tranzystorów n-p-n i p-n-p.

Widzimy, że na prądy wyjściowe i_E i i_C składają się dwa prądy: prąd własny oraz prąd ze źródła parametrycznego, proporcjonalnego do prądu złącza sąsiedniego. Prądy te ujęte są w klasycznym układzie równań Ebera-Molla. Dla tranzystora n-p-n równania E-M. mają postać

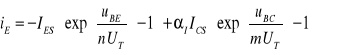
(9.1)

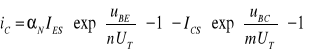
(9.2)

gdzie: I_ES - prąd rewersyjny nasycenia złącza emiterowego przy zwartym złączu kolektorowym (u_CB=0), I_CS - prąd rewersyjny nasycenia złącza kolektorowego przy zwartym złączu emiterowym (u_EB=0), n i m - współczynniki nieidealności (emisji) złącza - kolejno - emiterowego i kolektorowego, _N - współczynnik wzmocnienia prądowego tranzystora w konfiguracji wspólnej bazy (WB) normalnej pracy aktywnej, _I - współczynnik wzmocnienia prądowego tranzystora w konfiguracji WB inwersyjnej (zwrotnej) pracy aktywnej. Powyższe parametry są współzależne w tożsamości Onsagera

_N I_ES = _I I_CS ≡ I_S (9.3)

gdzie I_S jest tzw. transportowym prądem nasycenia w modelach komputerowych (np. SPICE). Każdy z nich można zatem wyznaczyć znając trzy pozostałe - jakkolwiek tożsamość (9.3) jest prawdziwa tylko przy symetrii geometrycznej tranzystora.

Korzystając z tożsamości Onsagera, równania E-M można przepisać przy pomocy tylko trzech parametrów _N, _I i I_S:

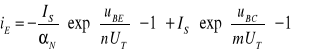
(9.4)

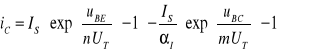
(9.5)

Obie powyższe pary równań E-M uproszczą się znacznie, jeżeli zdefiniujemy dwie wielkości

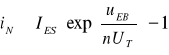
(9.6)

- jako prąd diody emiterowej dla aktywnej pracy normalnej tranzystora, przy u_BE>0,3V i u_BC<0, oraz

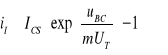
(9.7)

- jako prąd diody kolektorowej dla aktywnej pracy inwersyjnej tranzystora przy u_BE<0 i u_BC>0,3V. Zachowanie tych diod jest nieco inne niż normalnej, swobodnej diody złączowej p-n. W diodzie emiterowej złącze kolektorowe ze swym potencjałem kontaktowym zbiera prawie wszystkie nośniki mniejszościowe wstrzyknięte z emitera - rys.9.2. Dla wystarczająco dużych wartości napięcia u_BE= 0,3...0,6V prąd diody emiterowej można zapisać jako

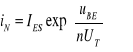
(9.8)

W ten sposób mamy najprostszy układ równań E-M

i_E = -i_N + α_Ii_I (9.9)

i_C = α_Ni_N - i_I (9.10)

Dwa równania Ebersa-Molla wraz z prawami Kirchhoffa dla tranzystora; prądowym (PPK)

i_B = -(i_C + i_E) (9.11)

oraz napięciowym (NPK)

u_CE = u_CB - u_BE=u_EB - u_BC (9.12)

są czterema niezależnymi równaniami tranzystora, które wiążą ze sobą jego sześć para- metrów zewnętrznych: i_C, i_E, i_B, u_BC, u_BE i u_CE. Z PPK otrzymujemy prąd bazy

i_B = -(i_E + i_C) = i_N(1 - α_N) + i_I(1 - _I) (9.13)

9.2. Metody wyznaczania parametrów równań Ebersa-Molla

W normalnej pracy aktywnej tranzystora złącze emiterowe jest spolaryzowane przepustowo, a złącze kolektorowe zaporowo. W takich warunkach prąd kolektorowy można określić przez prąd emiterowy

i_C = - _Ni_E - i_I(1 - _N_I) (9.14)

a uwzględniając, że u_CB <0, i w ten sposób i_I=-I_CS w (9.7), to następnie otrzymamy

i_C = - _Ni_E + I_CS(1 - _N_I) (9.15)

Podobnie dla rewersyjnej pracy aktywnej mamy

i_E = - _Ii_C + I_ES(1 - _N_I) (9.16)

Ostatnie dwa równania wskazują, że cztery parametry równań E-M: _N ,_I, I_ES oraz I_CS można wyznaczyć z pomiarów zależności i_C=i_C(i_E) w normalnej pracy aktywnej oraz według zależności i_E= i_E(i_C) w inwersyjnej pracy aktywnej tranzystora w konfiguracji WB - rys.9.3.

Z nachylenia pierwszej funkcji liniowej wyznaczymy _N, a ekstrapolując ją do osi i_E=0 odczytamy prąd zerowy I_CO płynący w obwodzie kolektora przy otwartym obwodzie emitera

(9.17)

W podobny sposób postępując przy inwersyjnej pracy aktywnej tranzystora otrzymamy zależność i_E = i_E(i_C) - według (9.16) - na podstawie której wyznaczymy współczynnik wzmocnienia _I oraz prąd zerowy I_EO przy pracy aktywnej

(9.18)

W konfiguracji WB można ponadto wyznaczyć współczynniki emisji n i m. Bowiem zwierając obwód kolektora ; dla u_BC= 0, z pierwszego równania E-M wynika, że i_E=i_F , i dla wystarczająco dużych wartości napięcia u_EB≥ 0,3 V zgodnie z zależnością (9.8) otrzymamy wyrażenie dla n

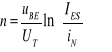
(9.19a)

albo korzystając z wykresu zależności lni_N=f(u_BE) - według rys.9.2. - współczynnik n wyznaczamy przyrostowo z nachylenia prostej

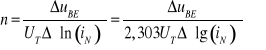
(9.19b)

Postępując podobnie przy pracy inwersyjnej tranzystora w konfiguracji WB przy u_BE=0, otrzymamy także, że

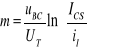
(9.20a)

albo

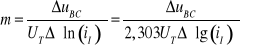
(9.20b)

gdzie i_I=i_C dla u_BC≥ 0,3 V.

Jednakże najczęściej tranzystor pracuje w konfiguracji wspólnego emitera WE, w której sterowany jest prądem bazy i_B - rys.9.4a. Jeżeli zatem skorzystamy z PPK wg (9.11) i zastąpimy prąd emiterowy w równaniu (9.15) prądem bazy i_B, to otrzymamy równanie kolektorowe dla WE

(9.21)

gdzie

(9.22)

jest współczynnikiem wzmocnienia prądu bazy w konfiguracji wspólnego emitera (WE). Zależność (9.21) jest podstawowym równaniem tranzystora dla tej konfiguracji, reprezentowanym schematem funkcjonalnym prądu bazy (rys.9.4b.), a jej podstawowe parametry wyznaczamy, wykreślając charakterystykę przejściową - rys.9.5.

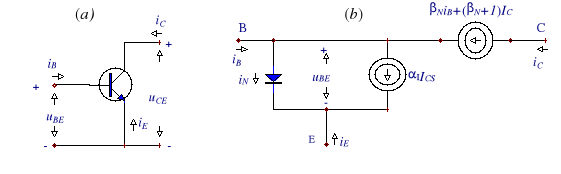
Rys.9.4. a -Tranzystor n-p-n w konfiguracji wspólnego emitera (WE), b - schemat funkcjonalny prądu bazy i_B.

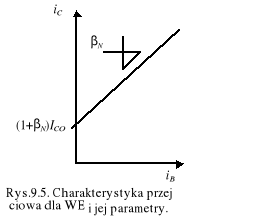
Podobnie dla inwersyjnej pracy aktywnej tranzystora - po odwróceniu ról diody emiterowej z diodą kolektorową - zdefiniujemy współczynnik inwersyjnego wzmocnienia bazy

(9.23)

Prąd zerowy kolektora I_CEO przy otwartej bazie w tranzystorze, który pracuje w konfiguracji WE (rys.9.4a) definiujemy następująco

(9.24)

Charakterystyki wejściowe dla konfiguracji WB są przybliżane zależnością

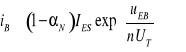
(9.25)

Dla wystarczająco dużych napięć na tranzystorze u_CE>0,3 V charakterystyki wyjściowe w konfiguracji WE wykazują jednak liniową zależność od u_CE (rys.9.6) ze współczynnikiem nachylenia 1/U_AN (efekt Early'ego)

(9.26a)

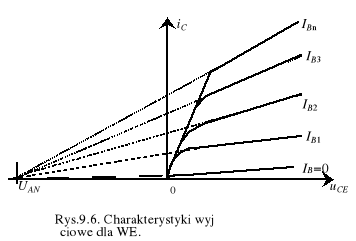
gdzie U_AN - napięcie Early'ego, które wyznaczamy z ekstrapolacji liniowej charakterystyk wyjściowych w zakresie nasycenia prądu kolektorowego do prostej i_C=0 (rys.9.6). Z tą prostą ekstrapolowane proste przecinają się w jednym punkcie U_AN, tylko wtedy gdy baza jest jednorodnie domieszkowana.

Odpowiednio ten sam typ zależności liniowej występuje w zakresie nasycenia w inwersyjnej pracy aktywnej i jest charakteryzowany napięciem Early'ego U_AI

(9.26b)

9.3. Model transportowy tranzystora

W symulacji komputerowej pracy tranzystora w konfiguracji WE prąd nasycenia I_S określany zależnością (9.3) jest jedynym parametrem modelu E-M dla obu złącz. W tym przypadku definiowane są prądy

i_EC ≡ _Ii_I (9.27)

oraz

i_CC ≡ _Ni_N (9.28)

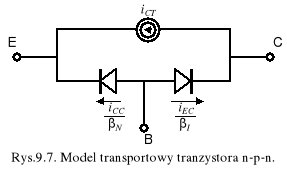
i teraz równania E-M przyjmują postać

(9.29)

(9.30)

gdzie

i_CT = i_CC - i_EC (9.31)

Na podstawie równań (9.29) i (9.30) oraz PPK w postaci (9.12) łatwo wykazać, że prąd bazy jest równy

(9.32)

które opisuje tzw. model transportowy tranzystora - rys.9.7. W tym modelu źródło prądowe reprezentuje nośniki mniejszościowe transportowane przez bazę, a i_CC i i_EC zależą od tego samego prądu I_S.

9.4. Przebieg ćwiczenia

Podczas ćwiczenia badany jest tranzystor małej mocy typu BC107 lub BF215. Pomiary wykonywane są pod kontrolą programu firmy Hewlett-Packard VEE, który zapewnia obsługę mierników firmowych za pomocą łącza HP-488 oraz obsługę mierników uniwersalnych METEX za pomocą łącza szeregowego RS232 (woltomierza i amperomierza) połączonych z komputerem IBM PC. Miernik HP344401 pracuje tutaj jednocześnie jako woltomierz na zaciskach Hi-Lo oraz amperomierz na zaciskach I-Lo. Program graficzny HP VEE pozwala obiektowo w postaci ikon zestawiać urządzenia w system pomiarowy na ekranie komputera, przesyłać i gromadzić wyniki pomiarów do/w komputerze, obrabiać matematycznie i bezpośrednio w czasie rzeczywistym przedstawiać w postaci wykresów. Właściwe programy do zbierania i obróbki danych pomiarowych dla poszczególnych etapów ćwiczenia 9. są umieszczone w katalogu WINDOWS (c:/win/vee_user). Są to kolejno: CW941, CW942, CW943 i CW944 - i w takiej kolejności będą uruchamiane po zmontowaniu rzeczywistych układów pomiarowych na module TM1 wg rysunków 9.8., 9.9., 9.10. i 9.11.

Po uruchomieniu programu i pojawieniu się na ekranie systemu pomiarowego należy uważnie go przestudiować: porównać ze schematem rzeczywistym, odczytać ewentualne komunikaty zgłaszające błędy i usterki, a następnie w ikonie TO FILE wpisać własną nazwę pliku, w którym będą umieszczane wyniki bieżących pomiarów. Pliki te znajdziemy w katalogu WYNIKI po zamknięciu każdego programu pomiarowego.

Program uruchamiamy klikając na ikonie RUN - w prawym górnym rogu ekranu.

Na wstępie zauważyć ikonę COUNTER- zliczającą od 1 do 4. W tym czasie komputer zbiera wyniki pomiarów odczytywane kolejno z mierników; dlatego wszelkie zmiany wielkości niezależnych (np. napięcia u_CE) lub parametrycznych, ustawianych przy pomocy potencjometrów (np. prądu bazy I_B), nie powinny być dokonywane w czasie jednego cyklu. Aby zmienić wielkość parametryczną, np. ustawić nową wartość I_B, najlepiej jest wstrzymać program ikoną STOP, ustawić nową wartość I_B, i potem wznowić działanie programu klikając na ikonie CONTinue. Każde użycie w tym czasie ikony RUN spowoduje wymazanie danych z adresowanego pliku oraz usunięcie wykresu z wirtualnego plotera !

9.4.1. Pomiary charakterystyk wyjściowych przy połączeniu normalnym

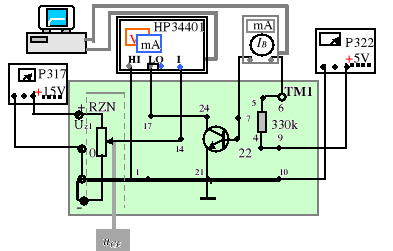
Jako pierwszy zestawiamy układ pomiarowy według rys.9.8 i uruchamiamy program CW941. Przy jego pomocy przeprowadzamy pomiary i_C=i_C(u_CE) przy I_B= const dla tranzystora w układzie wspólnego emitera przy kilku wartościach parametru I_B= 10, 15, 20, 25 μA .

Rys.9.8. Układ do pomiaru charakterystyki wyjściowej i_C = i_C(u_CE)

przy I_B=const

Wyniki pomiarów posłużą do wykreślenia charakterystyk wyjściowych i_C=i_C(u_CE) przy I_B=const na jednym układzie współrzędnych. Na podstawie ich przebiegu należy oszacować wartość napięcia Early'ego U_AN - wg (9.26a).

9.4.2. Pomiary charakterystyk wyjściowych przy połączeniu inwersyjnym

Zestawiamy na module TM1 układ wg rys.9.9 - podobny do układu z rys.9.8 - w którym tylko zamieniono miejscami wyprowadzenia emitera i kolektora tranzystora oraz zmniejszono wartość rezystora do z 300k do 10k, aby uzyskać większe prądy bazy Następnie, po uruchomieniu programu CW942 przeprowadzamy pomiary i_E= i_E(u_EC) przy I_B= const przy kilku znacznych wartościach parametru I_B = 15, 25 i 50 A . W połączeniu inwersyjnym nie należy przekraczać napięcia U_EC=5 V, aby nie przebić złącza baza-emiter. Tym razem uzyskane wyniki posłużą do wykreślenia charakterystyk wyjściowych i_E= i_E(u_EC) przy I_B=const. Na podstawie pomiarów w poprzednim podpunkcie oraz wzorów (9.21), (9.22), (9.23), (9.15) i (9.16) wyznaczamy parametry równań E-M: I_CS, I_ES, α_N, α_I. Używając wartości liczbowych tych współczynników napisać układ równań E-B - wg (9.1.i 9.2) oraz (9.3 i 9.4).

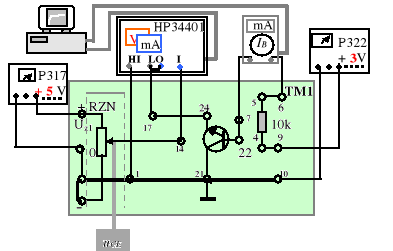
Rys.9.9. Układ do pomiaru inwersyjnej charakterystyki wyjściowej i_E= i_E(u_CE)

przy I_B=const

9.4.3. Określenie granicy pomiędzy obszarami aktywnymi i nasycenia

W celu dokładnego rozgraniczenia poszczególnych obszarów pracy należy zdjąć charakterystykę pomocniczą i_C= i_C(u_CE) przy U_CB=0 V. Dla przeprowadzenia pomiarów zestawiamy układ według rys.9.10. i uruchamiamy program CW943. Pomiary realizujemy dla zakresu i_C 20 mA.

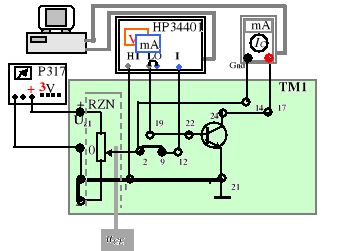
Rys.9.10. Układ do pomiaru charakterystyki wyjściowej i_C = i_C(u_BE) przy U_CB=0 (spadek napięcia na mikroamperomierzu do zaniedbania!)

9.4.4. Pomiary charakterystyki wejściowej i przejściowej w przy pracy normalnej

W celu określenia potencjału U_T odczytujemy z termometru temperaturę powietrza w laboratorium oraz zestawiamy układ wg rys.9.11. Uruchamiamy program CW944 i mierzymy jednocześnie charakterystykę wejściową i_B=i_B(u_BE) oraz charakterystykę przejściową
i_C = i_C(u_BE) przy U_CB = 3 V. Uwaga: Program kreśli wykres i_B=i_B(u_BE) z wartościami i_B pomnożonymi 300-krotnie !

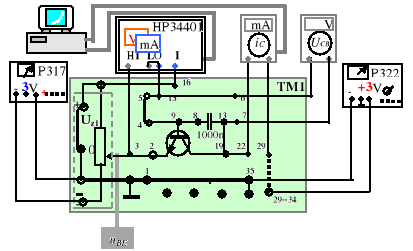
Rys.9.11. Układ do pomiarów charakterystyki wejściowej
i_B= i_B(u_BE) przy U_CB= 3 V

oraz charakterystyki przejściowej

i_C= i_C(u_BE) przy U_CB= 3 V

W sprawozdaniu sporządzamy następujące wykresy:

• i_C = i_C(u_BE) przy U_CB = 3 V w skali liniowo - liniowej,

• i_B = i_B(u_BE) przy U_CB = 3 V w skali liniowo - liniowej,

• β_N =β_N (i_C) przy U_CB = 3 V (β_N w skali liniowej, i_C w skali logarytmicznej),

• i_C = i_C(u_BE) i i_B = i_B(u_BE) przy U_CB = 3 V; na wspólnym rysunku w skali liniowo -

- logarytmicznej (oś napięć liniowa, oś prądów logarytmiczna).

Na podstawie sporządzonych wykresów należy określić prąd I_ES, współczynnik n oraz wartość współczynnika β_N.

9.4.5. Pomiary charakterystyki wejściowej i przejściowej w konfiguracji WE przy
połączeniu inwersyjnym

W układzie z rys.9.11. zamieniamy miejscami wyprowadzenia emitera i kolektora oraz uruchamiamy program CW944. Inwersyjną charakterystykę wejściową i_B=i_B(u_BC) oraz inwersyjną charakterystykę przejściową i_E = i_E(u_BC) należy zmierzyć przy U_EB= 3V.

Zmierzone charakterystyki nanosimy na wykresy charakterystyk i_C=i_C(u_BE) i i_B=i_B(u_BE) zmierzonych w poprzednim podpunkcie w skali liniowo-logarytmicznej, przyjmując następujące oznaczenia napięć i prądów tranzystora w połączeniu inwersyjnym: i_B, i_E = iⁱ_C, u_BC= uⁱ_BE, u_EC = uⁱ_CE.

Na podstawie wykresu charakterystyki przejściowej dla kierunku inwersyjnego można określić prąd nasycenia I_S oraz wartość współczynnika m. Porównać wyznaczone wartości prądów nasycenia dla kierunków normalnego i inwersyjnego. Porównać także wartości współczynników nieidealności n i m między sobą oraz z wartością oczekiwaną dla tranzystora idealnego. Następnie należy wyznaczyć maksymalną wartość inwersyjnego współczynnika wzmocnienia prądowego β_Imax i porównać ją z wartością β_Nmax.

W sprawozdaniu należy zestawić w tabeli komplet uzyskanych parametrów stałoprądowych badanego tranzystora, napisać dla niego układ równań Ebersa-Molla z właściwymi współczynnikami oraz przestawić wartości elementów zastępczych w modelu transportowym tranzystora.

1

64

---