14. ZŁĄCZOWE TRANZYSTORY POLOWE

14.1. Działanie złączowego tranzystora polowego

Schematyczny przekrój złączowego tranzystora polowego (n-JFET) podczas pracy przedstawia rys.14.1. Widzimy na nim, że przy polaryzacji zaporowej złącza p⁺-n (u_GS<0) jednorodny kanał typu n o wysokości a i długości L jest ograniczany przez warstwę zaporową o zmiennej wysokości H(x). Wysokość neutralnego kanału wynosi
i jest najmniejsza tuż przy drenie spolaryzowanym napięciem u_DS>0.

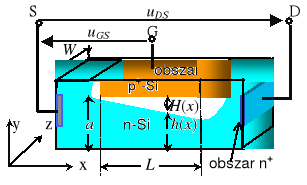
Rys.14.1. Przekrój złączowego tranzystora polowego z kanałem typu n

Zgodnie z teorią złącza, przy jednorodnie domieszkowanym donorami kanale typu n wysokość kanału elektronowego wynosi

(

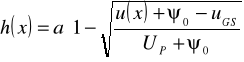
gdzie: ψ0  napięcie dyfuzyjne złącza p+-n, u(x) - spadek napięcia wzdłuż kanału o długości L i szerokości W, U_P - napięcie odcięcia (progowe), przy którym ciągłość obszaru neutralnego pomiędzy źródłem a drenem zostaje przerwana.

Wartość U_P najprościej jest określić, jeżeli kanał zostaje całkowicie odcięty na całej długości, czyli gdy przy x=0 mamy h(0)=0, co jest równoważne odcięciu prądu tranzystora (pinch-off). Na początku kanału u(0)=0 i szerokość warstwy zaporowej złącza jest funkcją tylko u_GS i ψ0 (ale nie zależy od u_DS). W tych warunkach z zależności (14.1) wynika, że odcięcie tranzystora JFET z kanałem typu n nastąpi przy napięciu na bramce

(14.2a)

Napięcie U_P jest określone zależnością

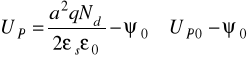
(14.2b

gdzie: Nd - koncentracja donorów, ψ₀ - potencjał dyfuzyjny złącza p⁺n, U_P0 - tzw. wewnętrzne napięcie odcięcia.

Prąd drenu jest tylko prądem unoszenia (dryftu), czyli strumieniem elektronów (-q) płynącym przez neutralny kanał o długości L i przekroju h(x)W w polu elektrycznym E =-duDS (x) /dx dla każdego x z zakresu [0, L]

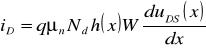
(14.3)

Scałkowanie powyższego równania - po podstawieniu za h(x) wyrażenia (14.1) - prowadzi do ogólnej zależności napięciowo-prądowej dla tranzystora z kanałem typu n:

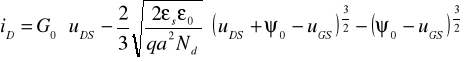
(14.4)

gdzie

(5.5)

jest konduktancją geometryczną kanału. Należy pamiętać, że zależność (14.4) została wyprowadzona dla ciągłego kanału neutralnego o długości L między źródłem a drenem (a więc, gdy u_GS<U_P), przez który przepływa prąd drenu i_D.

Dla tranzystorów z kanałem typu n napięcia u_GS­ i U_P są ujemne, a u_DS jest dodatnie, zaś dla tranzystora z kanałem typu p znaki tych napięć są przeciwne, zatem przy u_DS<0 także prąd i_D w zależności równoważnej (14.4) dla p-JFET będzie ujemny.

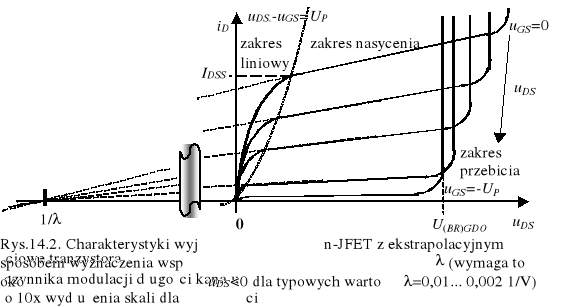
Dla małych napięć drenu, gdy uDS<<ψ_uGS, można wykazać, korzystając z rozwinięć dwumianowych zależności (14.4), że

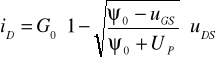
(14.6)

czyli prąd drenu jest liniową funkcją uDS w liniowym zakresie pracy tranzystora (rys.5.4). Gdy uGS= -U_P, to z powyższej zależności wynika, że iD= 0 i tranzystor jest w stanie odcięcia.

W miarę wzrostu różnicy potencjałów pomiędzy drenem a bramką zmniejsza się wysokość neutralnego kanału. Jeżeli przez U_DSS oznaczymy napięcie na drenie, przy którym warstwa zaporowa osiągnie wysokość a (co nastąpi na końcu drenu przy x=L), to w zależności (5.1) tym razem mamy h(L)=0 oraz u(L)=U_DSS. Stąd otrzymamy, że

(14.7)

UDSS jest taką wartością napięcia na drenie uDS, przy której na końcu kanału pole elektryczne jest na tyle duże, że w krzemie następuje nasycenie prędkości nośników. Dla u_DS=U_DSS funkcja (14.4) osiąga wartość maksymalną, którą nazywamy prądem nasycenia

(

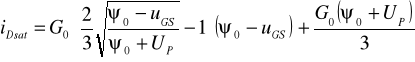
Przy dalszym wzroście u_DS >U_DSS długość efektywna neutralnego kanału L' jest mniejsza niż długość geometryczna (L'<L); obszar neutralny kanału ulega przerwaniu (p. rys.5.7), a tranzystor wchodzi w zakres nasycenia. W tym zakresie dla prądu drenu wstępnie przyjmujemy stałą wartość prądu nasycenia (14.8). Napięcie u_DS w zakresie nasycenia spełnia warunek

(14.9)

W tym zakresie napięć u_DS napięcie nasycenia drenu UDSS - wg (14.7) - i prąd nasycenia i_Dsat- wg (14.8) - zależą tylko od potencjału bramki uGS. Dla uGS= 0 i UDSS=UP prąd drenu ma wartość największą

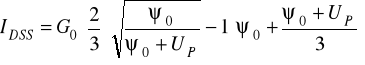
(14.10a)

Zwykle ψ0≤U_P/3, jeżeli zatem przyjmiemy, że ψ₀≈0 oraz skorzystamy z zależności (14.2) i (14.5), to prąd maksymalny w zakresie nasycenia możemy oszacować następująco

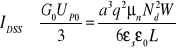
(14.10b)

W praktyce, zamiast dość złożonej zależności (14.8), prąd nasycenia obliczany jest według uproszczonej, kwadratowej zależności empirycznej

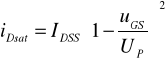
(14.11a)

Jednakże wraz ze wzrostem napięcia na drenie powyżej UDSS (uDS>UDSS) obserwuje się w rzeczywistych tranzystorach polowych liniowy przyrost prądu nasycenia w funkcji uDS, widoczny na charakterystykach wyjściowych (rys.14.2). Jest to tzw. efekt modulacji długości (skrócenia) kanału modelowany parametrem  [1/V] (rys.14.3). Jego wartość jest odwrotnością długości odcinka na osi ujemnej -u_DS, jaki wyznaczają styczne do charakterystyk wyjściowych w zakresie nasycenia, ekstrapolowane do przecięcia się z tą osią. Efekt modulacji kanału modyfikuje zależność (14.11a) do postaci

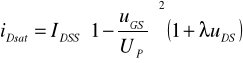
(14.11b)

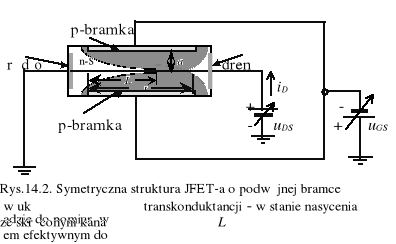
Jednakże dyskretne tranzystory JFET są elementami o czterech wyprowadzeniach zewnętrznych (rys.14.2). Obszar podłoża (body) jest dodatkową bramką, którą zwykle łączy się z bramką górną (joined-gate JFET). W układach scalonych jest ona na własnym potencjale UBS lub uziemiona UBS=0. W związku z tym, w idealizowanych modelach tych tranzystorów kanał ma wysokość 2a i jest jednostajnie i symetryczne zwężany z dwóch stron. Należy więc przyjąć, że przewodność kanału G0 jest dwukrotnie większa niż wartość określona wyrażeniem (14.5).

14.2. Parametry małosygnałowe

Definiujemy dwa podstawowe parametry małosygnałowe złączowego tranzystora polowego:

- konduktancję drenu (kanału)

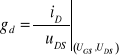
(14.12)

oraz transkonduktancję

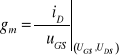
(14.13)

Z zależności (14.4) łatwo wykazać, że w zakresie liniowym:

(

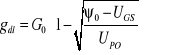
oraz

(

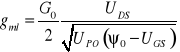
Natomiast w zakresie nasycenia transkonduktancja jest pochodną cząstkową równania (14.8) i wynosi

(

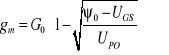
Dla idealnej kwadratowej zależności, dla której , podstawowy związek pomiędzy gm, IDSS i UPO jest postaci

(14.17)

Należy tutaj zauważyć, że zależności (14.14) i (14.16) są identyczne. Konduktacja wyjściowa zakresu liniowego jest zatem równa transkonduktacji zakresu nasycenia. Ponadto rezystancja szeregowa źródła rS redukuje wartość teoretyczną gm do wartości efektywnej

(14.18)

Empiryczna i prosta zależność kwadratowa prądu w zakresie nasycenia (14.11) jest określana dwoma parametrami: UPO i IDSS, które dla idealnego elementu łatwo wyznaczyć z wykresu liniowej zależności . W rzeczywistym elemencie należy uwzględnić efekt modulacji długości kanału  - i wówczas z definicji konduktancja kanału wynosi

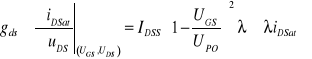
(14.19)

Konduktancja w zakresie nasycenia jest zatem proporcjonalna do prądu drenu, ale niezależna od uDS. Jest to intuicyjne możliwe do przyjęcia, bowiem zdolność uDS do mostkowania obszaru zubożonego pomiędzy źródłem a drenem oraz do modulacji długości aktywnego kanału będzie się zmniejszać, gdy szerokość tego zubożonego obszaru jest powiększana przez wzrost uGS - a tym samym spadek wartości iD. Uwzględniając to zjawisko, wzrost uDS jest równoważny wzrostowi uGS, zatem należy oczekiwać, że gm^→0, gdy uDS→∞ Konsekwencją tego zjawiska są różne wartości  otrzymywane z nachylenia rzeczywistych charakterystyk wyjściowych dla poszczególnych wartości UGS.

Złącza pomiędzy bramkami a kanałem mają skończoną pojemność złączową; przy średniej szerokości
wynosi ona

(14.20)

Przy napięciu uGS=0 oraz warunku odcięcia kanału;
, pojemność ta jest dwukrotnie większa

(14.21)

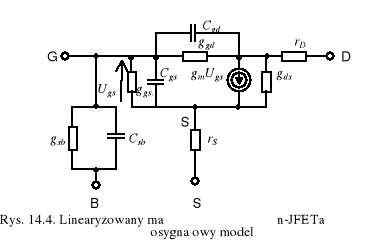
Pomimo rozłożonego wzdłuż kanału charakteru pojemności bramki jest ona reprezentowana dla uproszczenia w schemacie zastępczym JFET-a (rys.14.4) przez dwie wielkości: pojemność pomiędzy bramką i drenem Cgd oraz pojemność pomiędzy bramką a źródłem Cgs' - obie zależne od napięcia.

Ponadto w schemacie pojawia się pojemność pomiędzy drenem a źródłem Cds, uwarunkowana głównie bliskością obudowy elementu. Tranzystor polowy wykonany w układzie scalonym ma także na wejściu elementy związane z wpływem podłoża (B - body) konduktancję g_sb i pojemność C_sb.

Duża pojemność bramki ogranicza częstotliwość odcięcia tranzystora JFET, bowiem wynosi ona

14.22)

14.3. Przebieg ćwiczenia

Zasadniczym celem ćwiczenia jest wykreślenie charakterystyk wyjściowych i przejściowych wskazanych tranzystorów JFET na podstawie punktowych pomiarów napięciowo-prądowych. Wykresy te posłużą do wyznaczenia szeregu uprzednio zdefiniowanych parametrów małosygnałowych. W tym celu należy:

1. Zmontować układ pomiarowy według rys.14.5. Ustawić napięcie U_DS=5 V i regulując potencjometrem napięcie u_GS oszacować wartość napięcia progowego U_P jako napięcie u_GS, przy którym prąd drenu wynosi tylko 10 μA. Następnie należy zmierzyć i wykreślić charakterystyki i_D = i_D(u_DS) dla kilku stałych wartości U_GS.

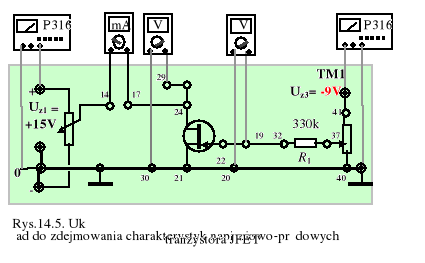
2. Wykreślić dla wybranej wartości U_DS=const charakterystykę przejściową jako funkcję:√i_D=f(u_GS) i na podstawie jej przebiegu i ekstrapolacji do punktu na osi napięciowej, w którym √i_D=0 wyznaczyć wartości parametrów I_DSS i U_P. Wykorzystać wyznaczoną wartość U_P do rozdzielenia zakresu liniowego i nasycenia na charakterystykach wyjściowych w układzie (i_D,u_DS).

3. Na podstawie wykresu uzyskanego w powyższym punkcie wyznaczyć metodą graficzną przebieg funkcji g_m= g_m(u_GS).

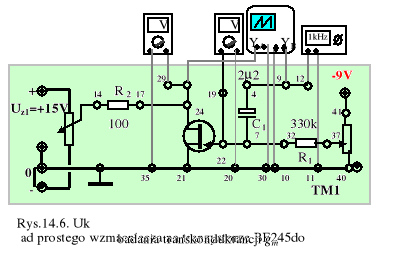
4. Zestawić na module TM-1 układ pomiarowy według rys.14.6. Jest to prosty wzmacniacz na tranzystorze BF245. Na wejście wzmacniacza podać z generatora napięcie piłokształtne o częstotliwości 1 kHz i wartości międzyszczytowej U_we,pp= 200 mV, a następnie zmierzyć na oscyloskopie wartość międzyszczytową napięcia wyjściowego dla wybranej w pkt.2. wartości U_DS i kilku wartości u_GS z przedziału U_P<u_GS<0. Uzyskane wyniki pozwalają wyznaczyć bezpośrednio zależność g_m = g_m(u_GS) - przy założeniu, że g_ds<<1/R₂.

5). Na wspólnym wykresie wykreślić zależności uzyskane z pomiarów w pkt.3. i 4. Na tym samym wykresie wyznaczyć także przebieg zależności teoretycznej g_m=g_m(u_GS) według zależności (14.16).

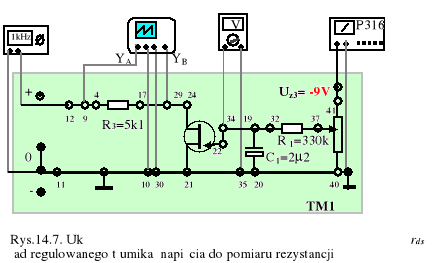
6). W układzie regulowanego tłumika napięcia z rys.14.7. ustawić piłokształtny przebieg napięcia o częstotliwości 1 kHz i wartości międzyszczytowej 100 mV, a następnie zmierzyć na ekranie oscyloskopu wartość międzyszczytową napięcia U_ds dla kilku wartości u_GS z przedziału U_P<u_GS<0. Na podstawie pomiarów wyznaczyć zależność r_ds= r_ds(u_GS) i nanieść ją na wspólny wykres z poprzednio otrzymanymi wynikami.

1

109

---