9. CHARAKTERYSTYKI STAŁOPRĄDOWE TRANZYSTORÓW BIPOLARNYCH
9.1. Model Ebersa - Molla
Tranzystor bipolarny jest przyrządem półprzewodnikowym, w którym dwa bliskie sobie złącza n-p i p-n, oddalone nie więcej niż 1 m, oddziałują na siebie poprzez iniekcję i ekstrakcję nośników mniejszościowych do bazy - wspólnego obszaru środkowego. Nośniki te tworzą tzw. prąd sprzężenia (prąd elektronowy In w strukturze złącz n-p-n).
Model Ebersa-Molla (E-M) przedstawia tranzystor jako kombinację dwóch parametrycznych źródeł prądowych, sterowanych sąsiednimi prądami diodowymi. Są to diody z prądami dyfuzyjnymi w obszarze bazy o przeciwsobnych potencjałach dyfuzyjnych na złączu emiterowym i złączu kolektorowym w układzie o wspólnej bazie (WB) - rys.9.1. W takiej konfiguracji nie ma wzmocnienia prądowego, ale poprzez podłączenie dużej rezystancji obciążenia można uzyskać wzmocnienie napięcia i mocy.
Rys.9.1. Modele Ebersa-Molla dla tranzystorów n-p-n i p-n-p.
Widzimy, że na prądy wyjściowe iE i iC składają się dwa prądy: prąd własny oraz prąd ze źródła parametrycznego, proporcjonalnego do prądu złącza sąsiedniego. Prądy te ujęte są w klasycznym układzie równań Ebera-Molla. Dla tranzystora n-p-n równania E-M. mają postać
(9.1)
(9.2)
gdzie: IES - prąd rewersyjny nasycenia złącza emiterowego przy zwartym złączu kolektorowym (uCB=0), ICS - prąd rewersyjny nasycenia złącza kolektorowego przy zwartym złączu emiterowym (uEB=0), n i m - współczynniki nieidealności (emisji) złącza - kolejno - emiterowego i kolektorowego, N - współczynnik wzmocnienia prądowego tranzystora w konfiguracji wspólnej bazy (WB) normalnej pracy aktywnej, I - współczynnik wzmocnienia prądowego tranzystora w konfiguracji WB inwersyjnej (zwrotnej) pracy aktywnej. Powyższe parametry są współzależne w tożsamości Onsagera
N IES = I ICS ≡ IS (9.3)
gdzie IS jest tzw. transportowym prądem nasycenia w modelach komputerowych (np. SPICE). Zatem każdy z nich można wyznaczyć znając trzy pozostałe - jakkolwiek tożsamość (9.3) jest prawdziwa tylko przy symetrii geometrycznej tranzystora.
Korzystając z tożsamości Onsagera, równania E-M można przepisać przy pomocy tylko trzech parametrów N, I i IS:
(9.4)
(9.5)
Obie powyższe pary równań E-M uproszczą się znacznie, jeżeli zdefiniujemy dwie wielkości
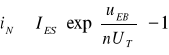
(9.6)
- jako prąd diody emiterowej dla aktywnej pracy normalnej tranzystora, przy uEB>0,3V i uCB<0, oraz
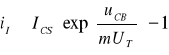
(9.7)
- jako prąd diody kolektorowej dla aktywnej pracy inwersyjnej tranzystora przy uEB<0 i uCB>0,3V. Zachowanie tych diod jest nieco inne niż normalnej, swobodnej diody złączowej p-n. W diodzie emiterowej złącze kolektorowe ze swym potencjałem kontaktowym zbiera prawie wszystkie nośniki mniejszościowe wstrzyknięte z emitera - rys.9.2. Dla wystarczająco dużych wartości napięcia uEB= 0,3...0,6V prąd diody emiterowej można zapisać jako
(9.8)
W ten sposób mamy najprostszy układ równań E-M
iE = -iN + αIiI (9.9)
iC = αNiN - iI (9.10)
Dwa równania Ebersa-Molla wraz z prawami Kirchhoffa dla tranzystora; prądowym (PPK)
iB = -(iC + iE) (9.11)
oraz napięciowym (NPK)
uCE = uCB - uBE (9.12)
są czterema niezależnymi równaniami tranzystora, które wiążą ze sobą jego sześć para- metrów zewnętrznych: iC, iE, iB, uCB, uEB i uCE. Z PPK otrzymujemy prąd bazy
iB = -(iE + iC) = iN(1 - αN) + iI(1 - I) (9.13)
9.2. Metody wyznaczania parametrów równań Ebersa-Molla
W normalnej pracy aktywnej tranzystora złącze emiterowe jest spolaryzowane przepustowo, a złącze kolektorowe zaporowo. W takich warunkach prąd kolektorowy można określić przez prąd emiterowy
iC = - NiE - iI(1 - NI) (9.14)
a uwzględniając, że uCB <0, i w ten sposób iI=-ICS w (9.7), to następnie otrzymamy
iC = - NiE + ICS(1 - NI) (9.15)
Podobnie dla rewersyjnej pracy aktywnej mamy
iE = - IiC + IES(1 - NI) (9.16)
Ostatnie dwa równania wskazują, że cztery parametry równań E-M: N ,I, IES oraz ICS można wyznaczyć z pomiarów zależności iC=iC(iE) w normalnej pracy aktywnej oraz według zależności iE= iE(iC) w inwersyjnej pracy aktywnej tranzystora w konfiguracji WB - rys.9.3.
Z nachylenia pierwszej funkcji liniowej wyznaczymy N, a ekstrapolując ją do osi iE=0 odczytamy prąd zerowy ICO płynący w obwodzie kolektora przy otwartym obwodzie emitera
(9.17)
W podobny sposób postępując przy inwersyjnej pracy aktywnej tranzystora otrzymamy zależność iE = iE(iC) - według (9.16) - na podstawie której wyznaczymy współczynnik wzmocnienia I oraz prąd zerowy IEO przy pracy aktywnej
(9.18)
W konfiguracji WB można ponadto wyznaczyć współczynniki emisji n i m. Bowiem zwierając obwód kolektora ; dla uCB= 0, z pierwszego równania E-M wynika, że iE=iF , i dla wystarczająco dużych wartości napięcia uEB≥ 0,3 V zgodnie z zależnością (9.8) otrzymamy wyrażenie dla n
(9.19a)
albo korzystając z wykresu zależności lniN=f(uEB) - według rys.9.2. - współczynnik n wyznaczamy przyrostowo z nachylenia prostej
(9.19b)
Postępując podobnie przy pracy inwersyjnej tranzystora w konfiguracji WB przy uEB=0, otrzymamy także, że
(9.20a)
albo
(9.20b)
gdzie iI=iC dla uCB≥ 0,3 V.
Jednakże najczęściej tranzystor pracuje w konfiguracji wspólnego emitera WE, w której sterowany jest prądem bazy iB - rys.9.4a. Jeżeli zatem skorzystamy z PPK wg (9.11) i zastąpimy prąd emiterowy w równaniu (9.15) prądem bazy iB, to otrzymamy równanie kolektorowe dla WE
(9.21)
gdzie
(9.22)
jest współczynnikiem wzmocnienia prądu bazy w konfiguracji wspólnego emitera (WE). Zależność (9.21) jest podstawowym równaniem tranzystora dla tej konfiguracji, reprezentowanym schematem funkcjonalnym prądu bazy (rys.9.4b.), a jej podstawowe parametry wyznaczamy, wykreślając charakterystykę przejściową - rys.9.5.
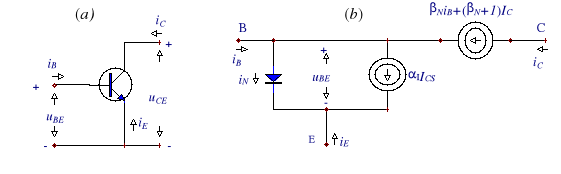
Rys.9.4. a -Tranzystor n-p-n w konfiguracji wspólnego emitera (WE), b - schemat funkcjonalny prądu bazy iB.
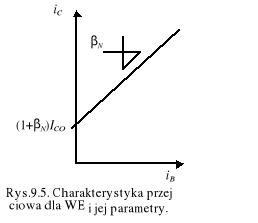
Podobnie dla inwersyjnej pracy aktywnej tranzystora - po odwróceniu ról diody emiterowej z diodą kolektorową - zdefiniujemy współczynnik inwersyjnego wzmocnienia bazy
(9.23)
Prąd zerowy kolektora ICEO przy otwartej bazie w tranzystorze, który pracuje w konfiguracji WE (rys.9.4a) definiujemy następująco
(9.24)
Charakterystyki wejściowe dla konfiguracji WB są przybliżane zależnością
(9.25)
Dla wystarczająco dużych napięć na tranzystorze uCE>0,3 V charakterystyki wyjściowe w konfiguracji WE wykazują jednak liniową zależność od uCE (rys.9.6) ze współczynnikiem nachylenia 1/UAN (efekt Early'ego)
(9.26a)
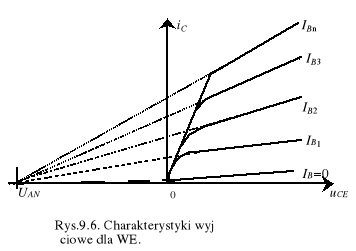
gdzie UAN - napięcie Early'ego, które wyznaczamy z ekstrapolacji liniowej charakterystyk wyjścio-wych w zakresie nasycenia prądu kolektorowego do prostej iC=0 (rys.9.6). Z tą prostą ekstra-polowane proste przecinają się w jednym punkcie UAN, tylko wtedy gdy baza jest jednorodnie domieszkowana.
Odpowiednio ten sam typ zależności liniowej występuje w zakresie nasycenia w inwersyjnej pracy aktywnej i jest charaktery- zowany napięciem Early'ego UAI
(9.26b)
9.3. Model transportowy tranzystora
W symulacji komputerowej pracy tranzystora w konfiguracji WE prąd nasycenia IS określany zależnością (9.3) jest jedynym parametrem modelu E-M dla obu złącz. W tym przypadku definiowane są prądy
iEC ≡ IiI (9.27)
oraz
iCC ≡ NiN (9.28)
i teraz równania E-M przyjmują postać
(9.29)
(9.30)
gdzie
iCT = iCC - iEC (9.31)
Na podstawie równań (9.29) i (9.30) oraz PPK w postaci (9.12) łatwo wykazać, że prąd bazy jest równy
(9.32)
które opisuje tzw. model transportowy tranzystora - rys.9.7. W tym modelu źródło prądowe reprezentuje nośniki mniejszościowe transportowane przez bazę, a iCC i iEC zależą od tego samego prądu IS.
9.4 Przebieg ćwiczenia
Podczas ćwiczenia badany jest tranzystor małej mocy typu BC107 lub BF215. Pomiary wykonywane są pod kontrolą programu LABORAT.EXE, który zapewnia obsługę dwóch mierników METEX (woltomierza i amperomierza) połączonych z komputerem IBM PC złączem RS232. Podczas obsługi programu potwierdzamy każdorazowo zachowanie wyników pomiarów w pamięci dla zmienionych nastaw naciskając ENTER. Plik wyjściowy zawiera wyniki przeprowadzonych pomiarów, które są argumentami i wartościami funkcji dla wykreślenia charakterystyk badanych elementów. W przypadku pomiarów przeprowadzanych z trzema przyrządami pomiarowymi, należy zanotować jedno ze wskazań jako parametr stały charakterystyki.
9.4.1. Pomiary charakterystyk wyjściowych przy połączeniu normalnym
Jako pierwszy zestawiamy układ pomiarowy według rys.9.8. i uruchamiamy program LABORAT.EXE z parametrem OUT_NOM.DAT. Przeprowadzamy pomiary iC=iC(uCE) przy IB = const dla tranzystora w układzie wspólnego emitera przy kilku wartościach parametru IB= 10, 15, 20, 25 μA .
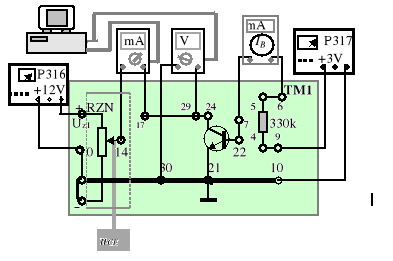
Rys.9.8. Układ do pomiaru charakterystyki wyjściowej iC = iC(uCE)
przy IB=const.
Wyniki pomiarów posłużą do wykreślenia charakterystyk wyjściowych iC=iC(uCE) przy IB=const na jednym układzie współrzędnych. Na podstawie ich przebiegu należy oszacować wartość napięcia Early'ego UAN - wg (9.26a).
9.4.2. Pomiary charakterystyk wyjściowych przy połączeniu inwersyjnym
Zestawiamy układ według rys.9.8, przy czym należy zamienić miejscami wyprowadzenia emitera i kolektora tranzystora. Następnie, po uruchomieniu programu LABORAT.EXE z parametrem OUT_INV.DAT, przeprowadzamy pomiary iE= iE(uEC) przy IB= const przy kilku wartościach parametru IB = 15 ... 25 μA . W połączeniu inwersyjnym nie należy przekraczać napięcia UEC=4 V, aby nie przebić złącza baza-emiter. Tym razem uzyskane wyniki posłużą do wykreślenia charakterystyk wyjściowych iE= iE(uEC) przy IB=const. Na podstawie pomiarów w poprzednim podpunkcie oraz wzorów (9.21), (9.22), (9.23), (9.15) i (9.16) wyznaczamy parametry równań E-M: ICS, IES, αN, αI. Używając wartości liczbowych tych współczynników napisać układ równań E-B - wg (9.1.i 9.2) oraz (9.3 i 9.4).
9.4.3. Określenie granicy pomiędzy obszarami aktywnymi i nasycenia
W celu dokładnego rozgraniczenia poszczególnych obszarów pracy należy zdjąć charakterystykę pomocniczą iC= iC(uCE) przy UCB=0 V. Dla przeprowadzenia pomiarów zestawiamy układ według rys.9.9. i ponownie uruchamiamy program LABORAT.EXE z parametrem OUT_0.DAT. Pomiary realizujemy dla zakresu iC 20mA.
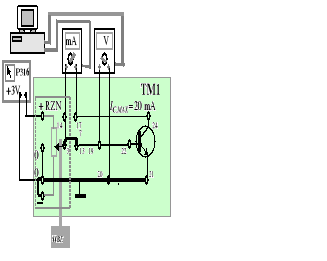
Rys.9.9. Układ do pomiaru charakterystyki wyjściowej iC = iC(uBE) przy UBC=0 (spadek napięcia na mikroamperomierzu do zaniedbania!)
9.4.4. Pomiary charakterystyki wejściowej i przejściowej w konfiguracji WE przy połączeniu normalnym
W celu określenia UT odczytujemy z termometru temperaturę powietrza w laboratorium oraz zestawiamy układ według rys.9.10. Program LABORAT.EXE uruchamiamy z parametrem TR_NOR.DAT i mierzymy jednocześnie charakterystykę wejściową iB= iB(uBE) przy UCB= 3 V dla tych samych wartości uBE oraz charakterystykę przejściową iC = iC(uBE) przy UCB = 3 V.
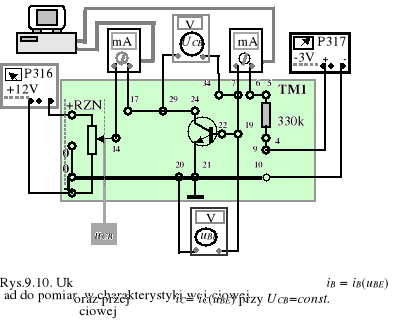
W sprawozdaniu sporządzamy następujące wykresy:
iC = iC(uBE) przy UCB = 3 V w skali liniowo - liniowej,
iB = iB(uBE) przy UCB = 3 V w skali liniowo - liniowej,
βN =βN (iC) przy UCB = 3 V (βN w skali liniowej, iC w skali logarytmicznej),
iC = iC(uBE) i iB = iB(uBE) przy UCB = 3 V; na wspólnym rysunku w skali liniowo -
- logarytmicznej (oś napięć liniowa, oś prądów logarytmiczna).
Na podstawie sporządzonych wykresów należy określić prąd IES, współczynnik n oraz wartość współczynnika βN.
9.4.5. Pomiary charakterystyki wejściowej i przejściowej w konfiguracji WE przy połączeniu inwersyjnym
W układzie z rys.9.10. zamieniamy miejscami wyprowadzenia emitera i kolektora oraz uruchamiamy program LABORAT.EXE z parametrem TR_INV.DAT. Inwersyjną charakterystykę wejściową iB=iB(uBC) należy zmierzyć przy UBE=3V, a inwersyjną charakterystykę przejściową iE = iE(uBC) przy UBE = -3 V.
Zmierzone charakterystyki nanosimy na wykresy charakterystyk iC=iC(uBE) i iB=iB(uBE) zmierzonych w poprzednim podpunkcie w skali liniowo-logarytmicznej, przyjmując następujące oznaczenia napięć i prądów tranzystora w połączeniu inwersyjnym: iB, iE = iiC, uBC= uiBE, uEC = uiCE.
Na podstawie wykresu charakterystyki przejściowej dla kierunku inwersyjnego można określić prąd nasycenia IS oraz wartość współczynnika m. Porównać wyznaczone wartości prądów nasycenia dla kierunków normalnego i inwersyjnego. Porównać także wartości współczynników nieidealności n i m między sobą oraz z wartością oczekiwaną dla tranzystora idealnego. Następnie należy wyznaczyć maksymalną wartość inwersyjnego współczynnika wzmocnienia prądowego βImax i porównać ją z wartością βNmax.
W sprawozdaniu należy zestawić w tabeli komplet uzyskanych parametrów stałoprądowych badanego tranzystora, napisać dla niego układ równań Ebersa-Molla z właściwymi współczynnikami oraz przestawić wartości elementów zastępczych w modelu transportowym tranzystora.
Wyszukiwarka
Podobne podstrony:
CWn12, 3 semestr, Przyrządy Półprzewodnikowe
SPIS-i-ORG 05, 3 semestr, Przyrządy Półprzewodnikowe
CW-OZNA, 3 semestr, Przyrządy Półprzewodnikowe
CWn14, 3 semestr, Przyrządy Półprzewodnikowe
CWn7, 3 semestr, Przyrządy Półprzewodnikowe
CWp13, 3 semestr, Przyrządy Półprzewodnikowe
CW7, 3 semestr, Przyrządy Półprzewodnikowe
CWL8, 3 semestr, Przyrządy Półprzewodnikowe
CW15Ub, 3 semestr, Przyrządy Półprzewodnikowe
CWpp15, 3 semestr, Przyrządy Półprzewodnikowe
CWn15, 3 semestr, Przyrządy Półprzewodnikowe
Cwn9VEE, 3 semestr, Przyrządy Półprzewodnikowe
CwS1, 3 semestr, Przyrządy Półprzewodnikowe
Przyrządy półprzewodnikowe (2)
Badanie optoelektrycznych właściwości przyrządów półprzewodnikowych 5 , LABORATORIUM FIZYCZNE
Materiałoznawstwo, Badanie właściwości materiałów i przyrządów półprzewodnikowych, POLITECHNIKA LUBE
Badanie optoelektrycznych właściwości przyrządów półprzewodnikowych 1 , Pomiar pierwszy
więcej podobnych podstron