15. TRANZYSTORY POLOWE MOS

15.1. Zarys teorii tranzystorów MOS-FET

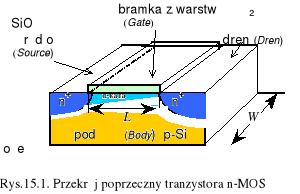
W tranzystorach polowych MOS-FET prąd płynący między źródłem a drenem w przypowierzchniowym kanale jest sterowany potencjałem elektrody bramki poprzez warstwę dielektryka - rys.15.1. Jest to prąd nośników większościowych. Kanał jest zwykle indukowany i tranzystor jest aktywny, gdy potencjał na bramce przekroczy wartość progową V_T. Poniżej tej wartości przez tranzystor płyną znikome prądy przypowierzchniowe, a tranzystor znajduje się w stanie odcięcia.

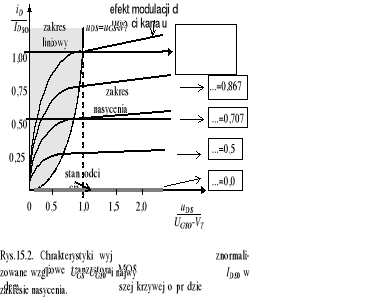
Przy stałych wartościach napięcia na bramce U_GS w układzie wspólnego źródła (WS) na charakterystykach prądowych drenu w układzie współrzędnych (i_D, u_DS) dla napięć u_DS mogą być wyszczególnione dwa zakresy: liniowy (nienasycenia) i nasycenia, rozdzielone napięciem u_DS=u_GS-V_T (rys.15.2). W naj- prostszym opisie tranzystora prąd drenu w zakresie liniowym jest kwadratową funkcją napięcia drenu u_DS

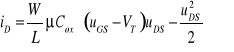
(15.1)

natomiast w zakresie nasycenia ma wartość stałą, niezależną od u_DS

15.2)

gdzie: W - szerokość, a L - długość kanału, μ - ruchliwość nośników w kanale, oraz C_ox - pojemność warstwy tlenkowej (izolacyjnej) bramki.

W tym najprostszym modelu tranzystora MOSFET (Sah - 1960) prąd przepływający przez kanał jest wyznaczony z równania dla składowej dryftowej transportu prądu nośników przez liniowo zawężający się kanał, powstały w obszarze ładunku przestrzennego. Jest to tzw. przybliżenie stopniowanego kanału; gdy pole elektryczne w kierunku prostopadłym do kanału jest znacz- nie większe niż natężenie pola wzdłuż kanału, w którym dryfują zaindukowane nośniki.

Pełny układ równań prądowych dla n-MOSFET-a przy niskich częstotliwościach pracy (i_G=0) jest następujący:

dla u_GS<V_T, u_DS>0 (stan odcięcia) (15.3a)

dla u_GS>V_T i 0<u_DS<u_GS -V_T (15.3b)

(zakres liniowy)

dla u_GS>V_T i u_DS>u_GS - V_T (15.3c)

(zakres nasycenia)

gdzie:
oraz V_T0>0 dla kanału indukowanego,

zaś V_T0<0 dla kanału zubożanego.

Gdzie ponadto wykorzystano tzw. parametry technologiczne tranzystorów:

k'=μC_ox - parametr transkonduktancyjny,

V_T0 - napięcie progowe przy napięciu podłoże-źródło u_BS=0,

γ - współczynnik objętościowy napięcia progowego,

λ - współczynnik modulacji długości kanału.

φ - potencjał powierzchniowy przy silnej inwersji półprzewodnika.

Dla tranzystorów p-MOSFET powyższe równania przyjmują postaci

dla u_GS>V_T, u_DS<0 (stan odcięcia) (15.4a)

dla u_GS<V_T i 0>u_DS>u_GS -V_T (15.4b)

(zakres liniowy)

dla u_GS<V_T i u_DS<u_GS - V_T (15.4c)

(zakres nasycenia)

gdzie:
oraz V_T0>0 dla kanału indukowanego,

zaś V_T0<0 dla kanału zubożanego

Współczynniki k', γ, λ i φ są dodatnie dla obu typów kanałów. Ponadto w projektowaniu tranzystorów używany jest tzw. parametr transkonduktancyjny przyrządu, nazywany też współczynnikiem wzmocnienia

(15.5)

W modelu Shichmana-Hodgesa prąd drenu w zakresie nasycenia przy wyprowadzaniu powyższych zależności został powiązany z napięciem na drenie u_DS, bowiem wraz ze wzrostem u_DS powyżej U_DSS (przy którym kanał traci ciągłość pomiędzy źródłem a drenem) poszerza się warstwa zubożona ładunku przestrzennego i skraca efektywna elektrycznie długość kanału L do L'. Także ze wzrostem u_DS rośnie ładunek warstwy inwersyjnej w pobliżu drenu. Zależności (15.3c) i (15.4c) mają charakter empiryczny: mała wartość λ=0,1...0,01 1/V potwierdza niewielki wpływ u_DS na i_D w zakresie nasycenia (rys.15.2). Aby uniknąć nieciągłości na granicy obszarów liniowego i nasycenia w charakterystykach prądowych czynnik (1+λu_DS) można dołączyć także do zależności dla zakresu liniowego. Wprowadza to oczywiście pewien błąd, jednakże nie znaczący w układach cyfrowych.

15.2. Metody wyznaczania parametrów charakterystycznych V_T, γ, k i λ

Pierwsze trzy parametry: V_T, γ i k wyznaczamy z przebiegu charakterystyk przejściowych, zmierzonych dla tranzystora, w którym u_GS=u_DS (rys.15.3.), i przedstawionych w postaci funkcji

f(u_GS=u_DS) (15.6)

Z przebiegu wykresów łatwo otrzymujemy: V_TO - z punktu odcięcia prądu przy i_D=0 dla u_SB=0, natomiast parametr k - z nachylenia prostej dla każdej stałej wartości U_SB, bowiem

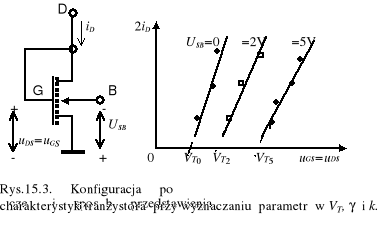
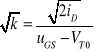
(15.7)

oraz

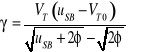
(15.8)

przy czym można przyjąć, że dla tranzystorów z krzemu 2φ=0,6 V.

Efekt modulacji kanału określamy na podstawie pomiarów charakterystyki wyjściowej tranzystora w konfiguracji połączeń zewnętrznych jak na rys.15.4a. w sposób przedstawiony na rys.15.4b. Bowiem łatwo zauważyć, że dla każdych dwóch punktów na charakterystyce (I_D,1,U_D,1) i (I_D,2,U_D,2) mamy

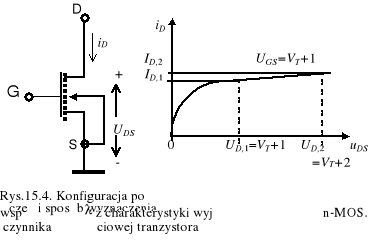
(15.9)

stąd

(15.10)

15.3. Wielkosygnałowy model zastępczy tranzystora MOS-FET

Rys.15.5. przedstawia model wielkosygnałowy tranzystora MOS zaproponowany przez Shichmana i Hodgesa. W modelu tym istotna jest zależność źródła napięciowego i_D od stałych napięć zewnętrznych, w tym także od napięcia pomiędzy podłożem a źródłem u_BS. Diody w tym schemacie reprezentują złącza n-p pomiędzy źródłem a podłożem oraz drenem a podłożem z prądami

(15.11a)

(15.11b)

I_s reprezentuje prądy upływności złącz podłożowych. r_D i r_S przedstawiają rezystancje drenu i źródła, które zwykle wynoszą około 50...100 om. Natomiast pojemności występujące w tym schemacie można podzielić na trzy grupy: pojemności barierowe C_BD i C_BS spolaryzowanych zaporowo złącz B-D i B-S, wspólne pojemności bramki C_GD, C_GS i C_GB (ich wielkość zależy od zakresu pracy tranzystora) oraz pojemności pasożytnicze (konstruk-cyjne), niezależne od zakresu pracy.

15.4. Małosygnałowy model tranzystora MOS-FET

Tranzystory MOS są typowymi elementami układów cyfrowych. Jednakże ostatnio są one także wykorzystywane w analogowych układach scalonych jako wzmacniacze małych sygnałów. Małosygnałowy model zastępczy, niezbędny przy analizie takich układów, uzyskuje się na bazie modelu wielkosygnałowego, w którym uwzględnione są małe, linearyzowane zaburzenia parametrów wokół określonych stałych ich wartości. W wyniku różniczkowania zależności prądowo-napięciowych (15.2), (15.3) i (15.4) w stałych punktach pracy tranzystora definiujemy jego parametry małosygnałowe:

- transkonduktancję

(15.12)

- konduktancję wyjściową

(15.13)

oraz transkonduktancję, wynikającą z wpływu napięcia u_BS na parametry kanału;

(15.14) Wartości tych małosygnałowych parametrów zależą od zakresu, w którym znajduje się punkt pracy tranzystora. Na przykład w zakresie nasycenia transkonduktancja g_m, zgodnie zależnością (15.2), wynosi

(15.15) Zależność parametrów małosygnałowych od warunków wielkosygnałowych w powyższym wyrażeniu jest zatem wyraźna. Podobnie, korzystając z definicji (15.14) stwierdzimy że, transkonduktancja g_mb wynosi

(15.16)

Jeżeli teraz skorzystamy z zależności (15.2) oraz zauważymy, że , to uzyskamy

(15.17)

gdzie η - współczynnik proporcjonalności. Ta transkonduktancja staje się ważna w przypadku, gdy wartość napięcia zmiennego u_BS jest różna od zera.

Łatwo też stwierdzić, że transkonduktancja wyjściowa kanału g_ds jest funkcją liniową prądu drenu

(15.18)

Można także wykazać, że g_ds zależy od długości kanału L dla tranzystorów o krótkim kanale.

Wartości rezystancji r_d i r_s są porównywalne z wartościami r_D i r_S w modelu wielkosygnałowym z rys.15.5. Podobnie przyjmuje się, że C_gs, C_gd, C_gb, C_bd i C_bs są takie same jak C_GS, C_GD, C_GB, C_BD i C_BS. Przy szacowaniu wielkości C_bd i C_bs można skorzystać z następujących przybliżeń:

(15.19)

(15.20)

15.5. Inwerter CMOS

Oba przedstawione powyżej typy tranzystorów polowych; n-MOS i p-MOS wykonane w technologii komplementarnej CMOS na jednym podłożu tworzą tzw. inwerter CMOS - najczęściej występujący obwód w układach scalonych (rys.15.6). Jest to struktura CMOS-inwertera wykonana w n-podłożu; dla tranzystora n-MOS utworzono tzw. p-studnię dyfuzyjną, w której z kolei wdyfundowano n-obszary źródła i drenu.

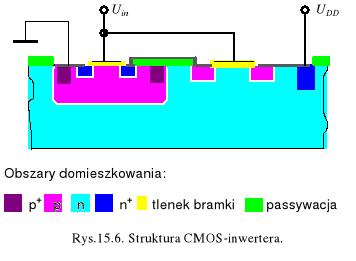
Podłoża (body) każdego z tranzystorów są połączone z ich źródłami, aby zapobiec polaryzacji przepustowej złącz p-n. Bramki tranzystorów są wspólne. Na bramki w układach logicznych podawany jest sygnał wejściowy zmieniający się od logicznego zera u_WE⁽⁰⁾≈0 do logicznej jedynki u_WE⁽¹⁾≈U_DD. Wyjściowy sygnał jest zbierany ze wspólnych drenów tranzystorów na pojemnościowym obciążeniu C_L - rys.15.7.

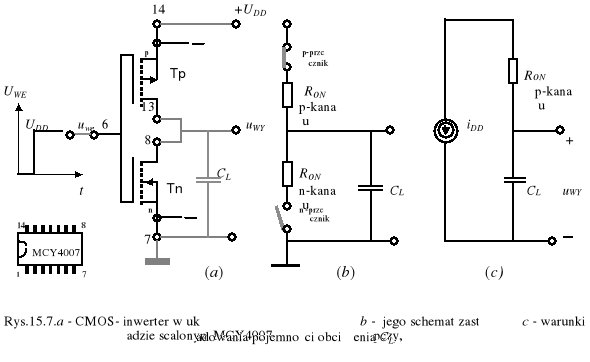
W układzie tym trudno jest odróżnić, który tranzystor jest sterujący, a który sterowany. Przy niskim poziomie napięcia na wejściu (logiczne 0) otwarty jest p-MOS, a n-MOS zamknięty, i na wyjściu mamy wysoki poziom napięcia (logiczna 1), bliski napięciu zasilania U_DD. Przy wysokim napięciu otwarty jest n-MOS, a p-MOS zamknięty, i wyjściowe napięcie jest niskie. Jest to typowa praca inwertera, w którym p-MOS spełnia rolę zmiennego obciążenia. Zamykanie jednego tranzystora otwiera drugi - i na odwrót (stąd: push and pull inverter). Taka praca układu jest związana z faktem, że

u_GS(n)+u_GS(p)=U_DD (15.21)

a spadek wartości u_GS jednego z tranzystorów powoduje zwiększenie u_GS drugiego. W efekcie charakterystyka przejściowa CMOS-inwertera wygląda jak na rys. 15.8.

Założymy na wstępie, że parametry tranzystorów są jednakowe, a prądy upływności bardzo małe. Ogólny warunek jest taki, że

V_Tn + V_Tp <U_DD<U_BO(n-p) (15.22)

Wtedy dla u_WE z zakresu 0<u_WE<V_Tn, tranzystor n-MOS jest zamkniety, a stanowiący obciążenie p-MOS otwarty, i wyjściowe napięcie wynosi u_WY=U_DD=U⁽¹⁾. Przy zwiększaniu u_WE od V_Tn do U_DD-V_Tp zachodzi ciągłe zamykanie p-tranzystora, otwieranie n-tranzystora i zmniejszanie napięcia wyjściowego u_WY. Przy u_WE=U_DD-V_Tp tranzystor obciążający jest zamknięty i u_WY =0=U⁽¹⁾. Zatem oba tranzystory włączają się nieokreślonym logicznym stanie pośrednim i wówczas prąd i_DD może wzrosnąć do niebezpiecznego poziomu (rys. 15.9).

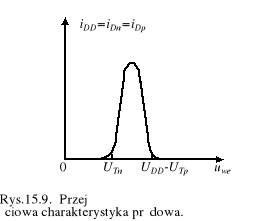
Bardzo ważne w układach logicznych czasy opóźnienia, narastania i opadania sygnału zależą także od napięcia zasilania. Najprostsze formy tych zależności dla CMOS-inwertera można otrzymać przy pominięciu pojemności własnych tranzystorów, przyjmując, że na wejście podawana jest logiczna jedynka U_we⁽¹⁾. Wtedy p-MOS zamyka się, a n-MOS otwiera, i na wyjściu uzyskujemy logiczną jedynkę: U_we⁽¹⁾. Przy przełączaniu tego stanu na stan niski; przy U_we⁽¹⁾ odwracają się stany tranzystorów, a C_L zaczyna ładować się poprzez p-MOS do napięcia +U_DD. Można przyjąć, że ten tranzystor pozostaje w zakresie nasycenia poprzez cały czas ładowania prądem

(15.23)

gdzie u_GS= U_DD. Jeżeli przyjąć, że V_Tp<<U_DD, to

(15.24)

Zatem prąd źródła w schemacie zastępczym inwertera (rys15.7c.) wynosi

(15.25)

Jest to stały prąd ładowania pojemności obciążenia C_L. Zatem

(15.26)

stąd

(15.27)

Jeżeli u_wy =U_DD, to stała czasowa układu t≡ wyniesie

(15.28)

Stąd wniosek, że czas narastania CMOS-inwertera jest odwrotnie proporcjonalny do napięcia zasilania U_DD.

15.6. Przebieg ćwiczenia

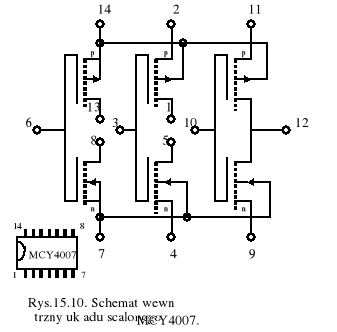
Celem ćwiczenia jest wyznaczenie charakterystyk napięciowo-prądowych tranzystorów n-MOS i p-MOS, tworzących pary komplementarne w układzie scalonym MCY74007 (rys.15.10) oraz określenie wartości parametrów elementów występujących w schemach zastępczych tych tranzystorów.

W tym celu należy:

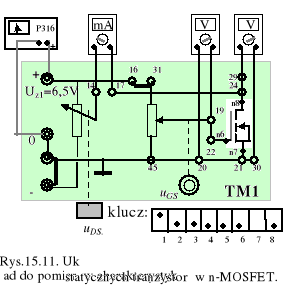
1. W układzie pomiarowym zestawionym na module TM1 według rys.15.11. zmierzyć charakterystykę przejściową i_D=i_D(u_GS) tranzystora n-MOS, dostępnego na wyprowadzeniach 6(G), 8 (D) i 7(S,B) układu MCY74007 w zakresie napięć dodatnich na bramce od U_GS=0 do U_GS= 5 V przy stałej wartości napięcia U_DS=5V. Sporządzić wykres funkcji √i_D=f(u_GS).

2. W tym samym układzie dokonać pomiarów potrzebnych do wykreślenia charakterystyk wyjściowych i_D= i_D(u_DS) w zakresie napięć od U_DS=0 do U_DS=5V przy stałych napięciach na bramce U_GS=2, 2,5, 3 i 4 V.

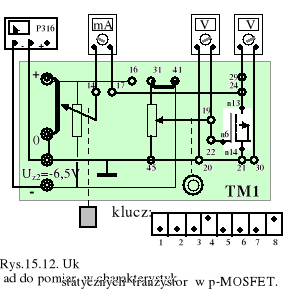
3. W układzie pomiarowym sporządzonym według rys.15.12. zmierzyć charakterystykę przejściową i_D= i_D(u_GS) tranzystora p-MOS, dostępnego na wyprowadzeniach 6(G), 13(D) i 14(S,B) układu MCY74007. Pomiary dokonujemy przy napięciach ujemnych U_DS= -5V oraz U_GS=-5 do U_GS= 0 V. Na podstawie zebranych wyników wykreślić zależność √i_D= f(u_GS).

4. Na podstawie zebranych pomiarów i przy pomocy wykresów wyznaczyć wartości parametrów elektrycznych elementów występujących w zastępczych schematach zastępczych tranzystorów oraz charakterystyczne parametry napięcia progowego V_T, γ , k i λ.

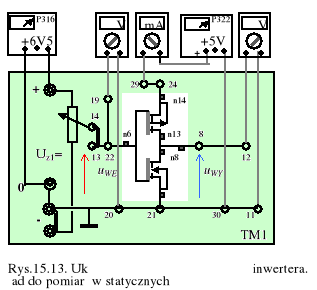
5. Zdjąć charakterystykę przejściową CMOS-inwertera z układu MCY40070N w układzie sporządzonym wg rys. 15.13. Z jej przebiegu odczytujemy wartości U_wy(1), U_wy(0) oraz U_we(1) i U_we(0). Wykreślić także charakterystykę prądu pobieranego przez inwerter w funkcji napięcia u_WE dla dwóch wartości napięcia zasilania U_DD = 5 i 10 V.

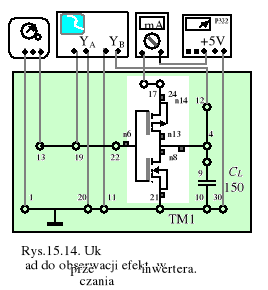
6. Obciążyć inwerter pojemnością C_L =150 pF i w układzie z rys.15.14. zaobserwować na oscyloskopie przełączanie inwertera sterowanego napięciem o przebiegu prostokątnym z amplitudą U_we(1)=5 V i częstotliwości od 100 do 500 kHz. Dokładnie odrysować przebiegi napięcia wyjściowego o czasach narastania t_r i opadania t_f przy zasilaniu układu 5 i 10 V. Korzystając z przedstawionych powyżej zależności oszacować i porównać z odczytami z oscyloskopu wartości tych czasów. Pamiętać, że sonda pomiarowa także stanowi dodatkowe obciążenie inwertera!

---