PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA
W PILE
SPRAWOZDANIE Z LABORATORIUM
Ćwiczenie nr 5 : Wyznaczenie przyspieszenia
ziemskiego za pomocą wahadła
matematycznego.
Data wykonania:
Wykonali:
1.Wstęp:
Ciążenie powszechne (grawitacja)
Prawo powszechnego ciążenia
Newton - 1665 spadanie ciał. Skoro istnieje siła przyciągania pomiędzy dowolnym ciałem i Ziemią, to musi istnieć siła między każdymi dwoma masami m1 i m2. Skoro siła jest proporcjonalna do masy ciała to musi być proporcjonalna do każdej z mas m1 i m2 oddzielnie czyli:
F ∼ m1m2
Newton zastanawiał się również, czy siła działająca na ciała będzie malała wraz ze wzrostem odległości. Doszedł do wniosku, że gdyby ciało znalazło się w odległości takiej jak Księżyc to będzie ono miało takie samo przyspieszenie jak Księżyc bowiem natura siły grawitacyjnej pomiędzy Ziemią i Księżycem jest taka sama jak pomiędzy Ziemią i każdym ciałem.
Newton wykonał takie obliczenia i wyciągnął wniosek, że siła przyciągania między dwoma masami maleje odwrotnie proporcjonalnie do kwadratu odległości między nimi (odległość między środkami mas). Sformułował więc prawo powszechnego ciążenia
![]()
Stałą proporcjonalności oznacza się G, więc
![]()
Newton oszacował wartość stałej G zakładając średnią gęstość Ziemi ρ = 5·103 kg/m3 (porównać to z gęstością pierwiastków z układu okresowego np. ρSi = 2.8·103 kg/m3, ρFe = 7.9·103 kg/m3).
Punktem wyjścia jest równanie:
![]()
Jeżeli weźmiemy r = RZ to otrzymamy:
![]()
Zgodnie z II zasadą Newtona F = ma, gdzie a = g.
Stąd
![]()
więc
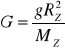
Wiemy, że MZ = ρVZ więc
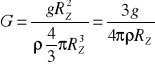
Uwzględniając RZ = 6.37·106 m otrzymamy G = 7.35·10-11 Nm2/kg2 co jest wartością tylko o 10% większą niż ogólnie przyjęta wartość 6.67·10-11 Nm2/kg2.
Porównując przyspieszenie grawitacyjne na orbicie Księżyca i na powierzchni Ziemi, Newton zakładał, że Ziemia zachowuje się tak jakby jej cała masa była skupiona w środku. Zgadywał, że tak ma być ale dowód matematyczny przeprowadził dopiero 20 lat później (wtedy też sformułował rachunek całkowy).
Równanie nazywa się prawem powszechnego ciążenia, ponieważ dokładnie to samo prawo stosuje się do wszystkich sił grawitacyjnych. To samo prawo wyjaśnia spadanie ciał na Ziemię, tłumaczy ruch planet, pozwala obliczyć ich masy i okresy obiegu.
Ruch drgający
Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić za pomocą funkcji sinus i cosinus. Ruch sinusoidalny jest powszechną formą ruchu obserwowaną w życiu codziennym i dlatego jest ważnym przedmiotem fizyki.
Siła harmoniczna
Działającą na ciało siłę, która jest proporcjonalna do przesunięcia ciała od początku układu i która jest skierowana ku początkowi układu, nazywamy siłą harmoniczną lub siłą sprężystości. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna jest wyrażona równaniem
F = - kx
gdzie x jest przesunięciem od położenia równowagi. To równanie opisuje siłę wywieraną przez rozciągniętą sprężynę o ile tylko sprężyna nie została rozciągnięta poza granicę sprężystości. To jest prawo Hooke'a.
Wartości maksymalne (amplitudy) odpowiednich wielkości wynoszą:
dla wychylenia A
dla prędkości ωA (występuje gdy x = 0)
dla przyspieszenia ω2A (występuje gdy x = A)
Okres drgań
Funkcja cosωt lub sinωt powtarza się po czasie T dla którego ωT = 2π. Ta szczególna wartość czasu jest zdefiniowana jako okres T
T = 2π/ω
Liczba drgań w czasie t jest równa
n = t/T
Liczba drgań w jednostce czasu
![]()
Lewa strona równania jest z definicji częstotliwością drgań f
![]()
Dla ruchu harmonicznego więc otrzymujemy
![]()
Zwróćmy uwagę, że okres drgań harmonicznych T jest niezależny od amplitudy drgań A. Tę właściwość drgań harmonicznych prostych zauważył Galileusz i wykorzystał ją do skonstruowania zegara wahadłowego.
Wahadła
Wahadło proste
Wahadło proste jest to wyidealizowane ciało o masie punktowej, zawieszone na cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy.
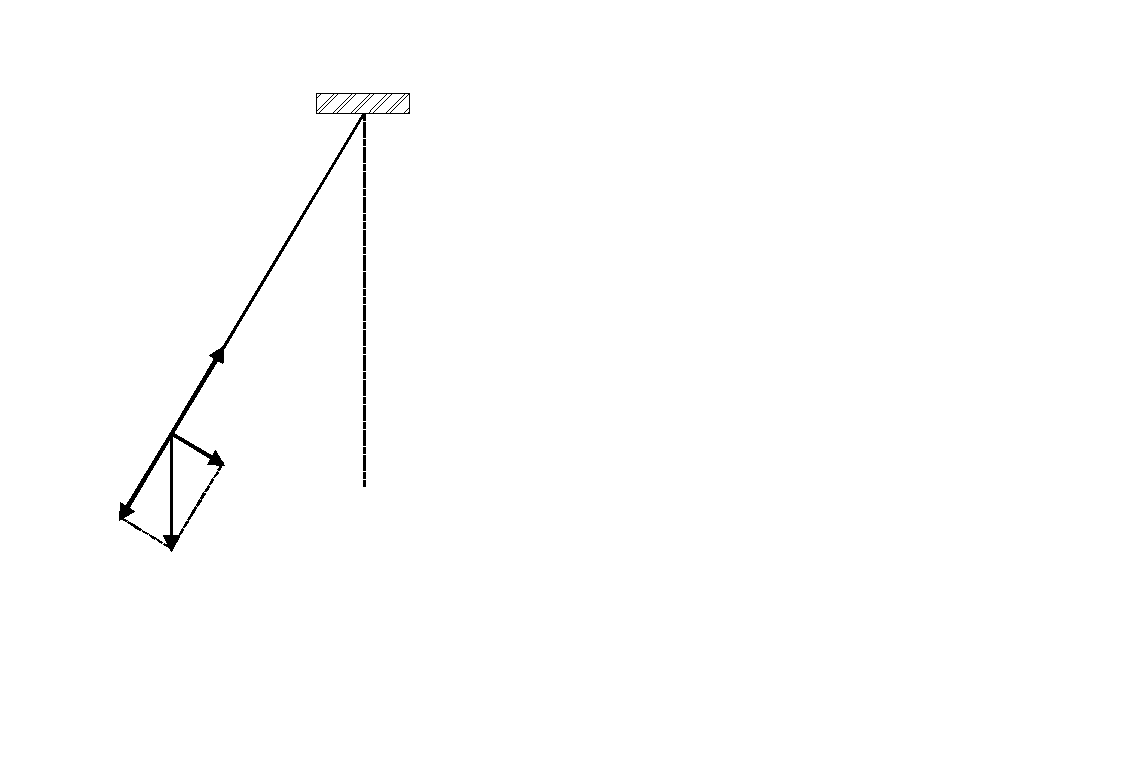
Rysunek przedstawia wahadło o długości l i masie m, odchylone o kąt θ od pionu. Na masę m działają: siła przyciągania grawitacyjnego mg i naprężenia nici N. Siłę mg rozkładamy na składową radialną i styczną. Składowa styczna jest siłą przywracającą równowagę układu i sprowadza masę m do położenia równowagi. Siła ta wynosi
F = mgsinθ
Podkreślmy, że siła jest proporcjonalna do sinθ, a nie do θ, więc nie jest to ruch prosty harmoniczny. Jeżeli jednak kąt θ jest mały (mniejszy niż 10°) to sinθ jest bardzo bliski 0 (różnica mniejsza niż 0.5%). Przemieszczenie wzdłuż łuku (z miary łukowej kąta) wynosi x = 10. Przyjmując zatem, że sinθ ≅0 otrzymujemy
![]()
Siła F jest więc proporcjonalna do przemieszczenia (ze znakiem "-"). Jest to kryterium ruchu harmonicznego. Stała mg/l określa stałą k w równaniu F = - kx. Przy małej amplitudzie okres wahadła prostego wynosi więc
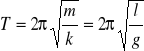
Zauważmy, że okres wahadła nie zależy od amplitudy i od masy wahadła.
Wahadło fizyczne
Dowolne ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi przechodzącej przez to ciało nazywamy wahadłem fizycznym.
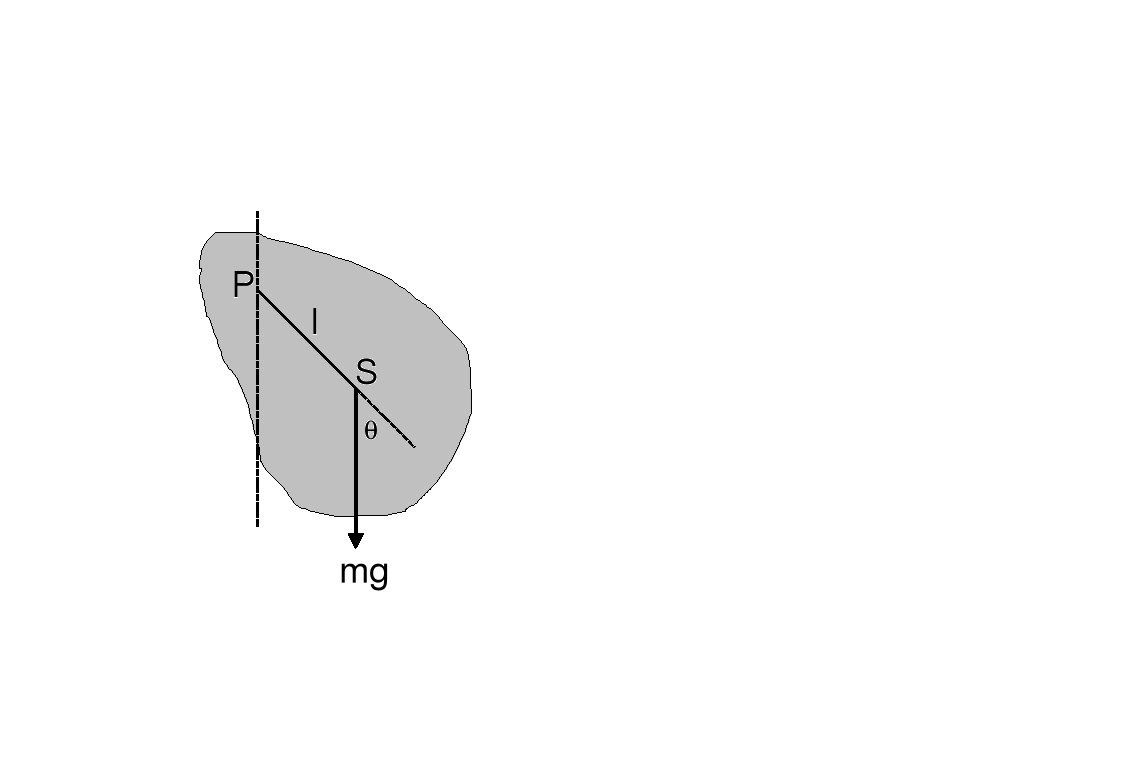
P jest punktem zawieszenia ciała, a punkt S, znajdujący się w odległości l od punkt P, jest środkiem masy. Moment siły τ działający na ciało wynosi
τ = - mglsinθ
Korzystając ze związku
τ = Iα =I(d2θ /dt2)
otrzymujemy
![]()
Dla małych wychyleń, dla których sinθ ≅ θ dostajemy równanie
![]()
To równanie ma tę samą postać co równanie dla ruchu harmonicznego więc
![]()
lub
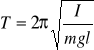
Jako przypadek szczególny rozpatrzmy masę punktową zawieszoną na nici o długości l. Wówczas I = ml2 i otrzymujemy znany wzór dla wahadła prostego
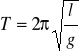
Wahadło fizyczne stosuje się do precyzyjnych pomiarów przyspieszenia g.
Wahadło matematyczne
Wahadłem matematycznym nazywamy punkt materialny
o masie „m” zawieszony na nierozciągliwej i nieważkiej
nici o długości „l” . Inaczej mówiąc jest to wahadło
doskonałe.
2.Wzory:
równanie ruchu harmonicznego
![]()
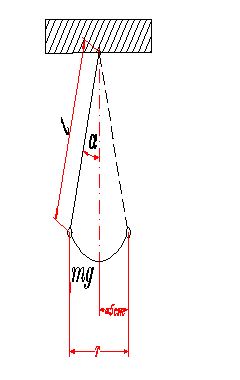
częstość drgań
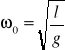
![]()
okres drgań
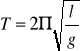
![]()
t- czas
n- ilość pełnych wychyleń
przyspieszenie ziemskie
![]()
l-długość wahadła (dł. sznurka + promień kulki)
3.Przebieg doświadczenia:
Zawieszamy kulkę na cienkiej nici o długościach podanych
w tabeli. Mierzymy długość wahadła od punktu zawieszenia do środka kulki za pomocą zwijanej miary metalowej.
Aby dokładnie wyznaczyć T, mierzymy czas trwania 10 okresów, a następnie z wzoru na okres drgań otrzymujemy czas trwania jednego pełnego wahnięcia.
Do pomiaru czasu używamy stopera, który pozwala mierzyć czas z dokładnością do 0,01 s. Liczymy kolejne przejścia kulki przez jedno z położeń skrajnych.
L.p. |
Długość l |
Czas t |
Okres T |
Przyspieszenie g |
A |
1,214 |
21 |
2,1 |
10,86 |
B |
0,919 |
17,5 |
1,75 |
11,84 |
C |
0,636 |
15,8 |
1,58 |
10,05 |
4.Obliczenie błędów:
- błąd długości ![]()
![]()
- błąd okresu ![]()
Obliczamy błąd względny:
![]()
Dla A: ![]()
![]()
B: ![]()
C: ![]()
Obliczamy błąd bezwzględny:
![]()
Dla A: ![]()
B: ![]()
C: ![]()
Ostatecznie:
![]()
![]()
![]()
![]()
4.Wnioski:
Największy wpływ na wielkość błędu ma w naszym przypadku refleks mierzącego (tzn. nie jednoczesne włączenie stopera i puszczenie kulki ). W obliczeniach należy również uwzględnić błąd paralaksy przy mierzeniu długości wahadła. Podobnie duży wpływ na ów błąd ma liczba mierzonych okresów. Gdyby liczbę tę zwiększyć otrzymany wynik byłby bliższy oczekiwanego 9.81m/s2.
1
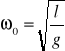
Wyszukiwarka
Podobne podstrony:
Przyspieszenie ziemskie, Fizyka
CW.1-Wyznaczenie przyspieszenia ziemskiego wahadla, 1 STUDIA - Informatyka Politechnika Koszalińska,
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, fizyka lab
wyznaczanie przyspieszenia ziemskiego, Politechnika Opolska, 2 semestr, Fizyka - Laboratorium, fizyk
Fizyka Laborka temat 1 Pomiar przyśpieszenia ziemskiego metodą?ssela
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła pros, Fizyka
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, 101B , Fizyka 101
Fizyka& wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
Fizyka- Pomiar przyspieszenia ziemskiego ziemskiego zahadłem, ĆWICZENIE NR1
cw 10 - Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego, Sprawozdania jakieś, F
więcej podobnych podstron