CAŁKI NIEOZNACZONE

Funkcją pierwotną funkcji
w przedziale
nazywamy każdą funkcję
taką, że

dla każdego
z przedziału
.

Dwie funkcje mające w danym przedziale tę samą skończoną pochodną mogą się różnić co najwyżej o stałą.

Całką nieoznaczoną funkcji
oznaczaną symbolem
nazywamy wyrażenie
, gdzie
jest funkcją pierwotną funkcji
, a
jest dowolną stałą. Mamy więc

, gdzie

Zapis
jest więc skrótem pytania: jakiej to funkcji pochodną jest funkcja f(x), a dx w zapisie informuje o zmiennej, względem której całkujemy.

Podstawowe wzory rachunku całkowego

1.
2.

Kilka szczególnych przypadków z różnym a to:

• dla
  :
  ;

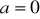
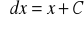
• dla
  :
  ;

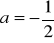
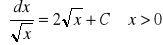
• dla
  :
  .

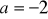
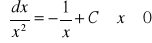
3.
4.
. 5.

6.
7.
8.
9.
10.

Własności całek nieoznaczonych:

1. Stały czynnik można wynieść przed znak całki, tzn.:

2. Całka sumy równa się sumie całek, (addytywność całki względem sumy podcałkowej) tzn.

(podobnie jest z różnicą - na podstawie punktu 1)

Metody całkowania

1. (Całkowanie przez części ) Jeżeli
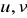
   są funkcjami zmiennej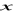
   mającymi ciągłą pochodną, to

2. (Całkowanie przez podstawienie) Jeżeli dla
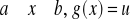
   jest funkcją mającą ciągłą pochodną oraz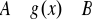
   , a funkcja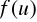
   jest ciągła w przedziale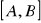
   , to

przy czym po scałkowaniu prawej strony należy w otrzymanym wyniku podstawić
.

Własność ogólna

Jeśli
to

CAŁKA OZNACZONA

Całkę oznaczoną funkcji
w przedziale
oznaczamy symbolem :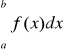
.

INTERPRETACJA GEOMETRYCZNA CAŁKI OZNACZONEJ

Jeżeli w przedziale
jest
to pole obszaru ograniczonego krzywą
, odcinkiem osi
oraz prostymi
równa się całce oznaczonej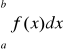
. Jeżeli zaś w przedziale
jest
, to analogiczne pole równa się -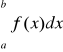
.

Związek między całką oznaczoną i nieoznaczoną. (Twierdzenie Newtona-Leibniza)

Jeżeli
jest funkcją pierwotną funkcji
, ciągłej w przedziale
, tzn. jeśli
, to zachodzi wzór: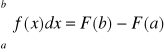
=
.

DŁUGOŚĆ ŁUKU KRZYWEJ

Jeżeli krzywa wyznaczona jest równaniem postaci
, przy czym funkcja
ma w przedziale
ciągłą pochodną, to długość łuku w tym przedziale wyraża się wzorem:

.

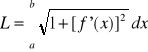
OBJĘTOŚĆ I POLE POWIERZCHNI BRYŁ OBROTOWYCH

Niech dany będzie łuk AB krzywej o równaniu
gdzie
jest funkcją ciągłą i nieujemną w przedziale
. Wówczas objętość bryły obrotowej ograniczonej powierzchnią powstałą w wyniku obrotu łuku AB dookoła osi Ox wyraża się wzorem: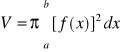
, gdy obrót wokół osi Oy: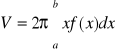

Pole powierzchni obrotowej powstałej przez obrót łuku AB wokół osi Ox obliczamy według wzoru:

.

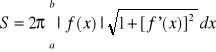
.CAŁKI NIEWŁAŚCIWE

CAŁKI FUNKCJI NIEOGRANICZONYCH

Jeżeli funkcja
jest ograniczona i całkowalna w każdym przedziale
,
oraz w każdym przedziale
i jeżeli istnieją granice:

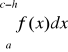
oraz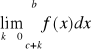
,

to sumę tych granic nazywamy całką niewłaściwą funkcji
w przedziale
i oznaczamy symbolem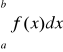
. Jeżeli któraś z powyższych granic nie istnieje, to mówimy, że całka niewłaściwa jest rozbieżna.

CAŁKI OZNACZONE W PRZEDZIALE NIESKOŃCZONYM.

Jeżeli funkcja
jest ograniczona i całkowalna w każdym przedziale skończonym
(
- ustalone,
- dowolne ) oraz istnieje granica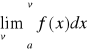
, to granicę tę nazywamy całką niewłaściwą funkcji
w przedziale
i oznaczamy symbolem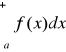
.

Analogicznie określa się znaczenie symbolu :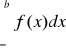
jako granicę
.

1

---