f(t) =![]()
![]()
cos ![]()
ω0 t dla t ![]()
τ/2 ![]()
Wprowadzenie do systemów telekomunikacyjnych
Seminarium rok 2000/2001
Prowadzący: dr inż. Wojciech J. Krzysztofik
Wykonał: Wojciech Radajewicz (nr ind.: 94884; rok stud./Gr.: III/TEL)
Zadanie Z 1/10
I. Treść zadania
Określić transformatę Fouriera impulsów w. cz.
f(t) =![]()
![]()
cos ![]()
ω0 t dla t ![]()
τ/2 ![]()
0 dla t > τ/2
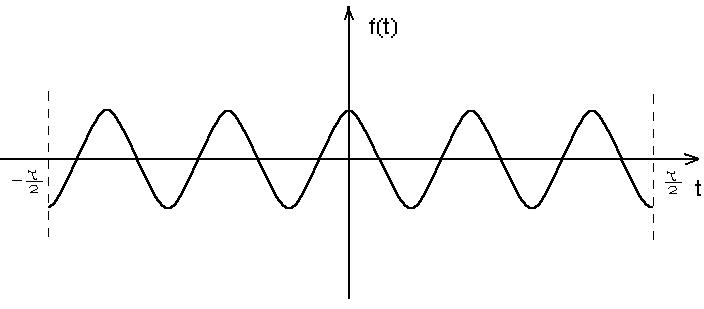
Naszkicować ich charakterystykę gęstości widmowej. Dla jakich częstotliwości funkcja ta jest równa 0?
II. Wprowadzenie teoretyczne
Liniowe przekształcenie Fouriera pomaga w rozwiązywaniu wielu zagadnień dotyczących układów liniowych i jest stosowane w różnych dziedzinach nauki. Zastosowanie tego przekształcenia umożliwia rozwiązywanie zagadnień zarówno fizycznych jak i matematycznych. Ponieważ można zmierzyć przebiegi i widma zjawisk elektrycznych np. odpowiednio za pomocą oscyloskopu, a także spektroskopu. Zatem transformaty Fouriera nie są jedynie przekształceniami matematycznymi, ale mają również określony sens fizyczny, skoro widma są transformatami Fouriera przebiegów fizycznych.
Ciągłym przekształceniem Fouriera dokonanym nad funkcją f(t) nazywamy przekształcenie całkowe postaci
F(ω)=![]()
f(t) e-jωt dt
Odwrotnym przekształceniem Fouriera nazywamy przekształcenie
f(t)=![]()
f(ω) ejωt ![]()
.
Transformata Fouriera funkcji f(t) istnieje, jeżeli f(t) jest bezwzględnie całkowalna w przedziale (-∞;+∞), tzn.
![]()
f(t)dt < ∞.
Przez przekształcenie Fouriera funkcji f(t) można przyporządkować transformatę F(ω), będącą funkcją zespoloną zmiennej rzeczywistej ω. Wobec tego można zapisać, że
F(ω) = F(ω) ejϕ(ω), gdzie ϕ(ω) = arg F(ω). Przebieg F(ω) w funkcji ω nazywa się ciągłym widmem amplitudowym, przebieg ϕ(ω) ciągłym widmem fazowym funkcji f(t).
W powyższym zadaniu muszę określić transformatę Fouriera dla funkcji cos ω0t. Dlatego niezbędne jest skorzystanie ze wzoru Eulera:
cos ω0t = ![]()
, a także z poniższych własności przekształcenia Fouriera:
![]()
= 2Πδ(ω-ω0),
δ(t-t0) = ![]()
F(ω) = ![]()
,
F{δ(t)} = 1,
δ(t) ↔ F(ω),
1 ↔ 2Πδ(-ω),
![]()
↔ δ(t-t0),
![]()
↔ 2Π δ(t-t0) ⇔ ![]()
= 2Π δ(ω-ω0),
cos ω0t = ![]()
= Π[δ(ω-ω0) + δ(ω+ω0)].
III. Rozwiązanie
Określam transformatę Fouriera dla zadanej funkcji.
F(ω)=![]()
f(t) e-jωt dt = ![]()
cos ω0t e-jωt dt = ![]()
![]()
( ![]()
+![]()
)![]()
![]()
= ![]()
![]()
![]()
+ ![]()
![]()
![]()
= ![]()
![]()
-![]()
![]()
= ![]()
(![]()
- ![]()
) - ![]()
(![]()
- -![]()
) = ![]()
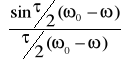
+![]()
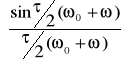
= =![]()
![]()
W obliczeniach skorzystałem ze wzoru Eulera na sin x= 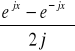
. Sa(x) oznacza ![]()
.
Poniżej przedstawiam wykres gęstości widmowej F=f(ω)dla dla określonego przebiegu w.cz., oraz obliczenia przy jakich częstotliwościach funkcja F(ω) przyjmuje wartość 0.
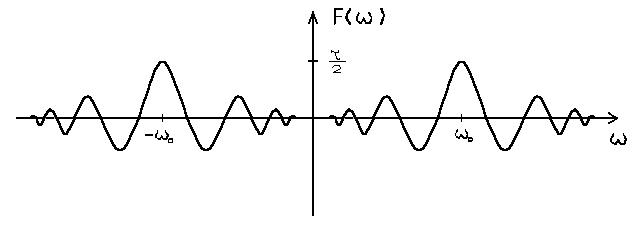
Funkcja F(ω) jest równa 0 ⇔ gdy ![]()
![]()
, gdzie k∈Z
ω=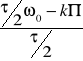
, gdzie ω0=![]()
ω=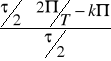
; ω=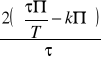
; ω=![]()
[![]()
]
ω=2Πf ; ![]()
=2Πf ; f=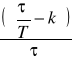
=![]()
[Hz] .
IV. Wnioski
Jak widać z obliczonych wyników transformata zadanych impulsów w.cz. jest funkcją skomplikowaną. F(ω)=![]()
![]()
Dlatego wykres zostal wykonany z pewnym przybliżeniem. Charakterystyka gęstości widmowej jest funkcją parzystą i osiąga zera dla czestotliwości f=![]()
, gdzie k∈Z.
1