Politechnika Białostocka

Wydział Elektryczny

Katedra Promieniowania Optycznego

Instrukcja do zajęć laboratoryjnych z przedmiotu

Podstawy Techniki Świetlnej

Ćwiczenie numer 4

Podstawowe zależności fotometryczne

Opracował: dr inż. Krzysztof Zaremba

2008

Zawartość instrukcji:

1. Wiadomości podstawowe 3

2. Cel i zakres ćwiczenia laboratoryjnego 4

3. Metodyka badań 5

4. Wymagania BHP 5

5. Sprawozdanie studenckie 6

6. Pytania kontrolne 6

7. Literatura 6

1. Wiadomości podstawowe

Strumień świetlny jest szybkością, z jaką promieniowanie świetlne jest emitowane przez źródło światła, czyli jest mocą tego promieniowania ocenianą pod względem możliwości wywoływania wrażenia wzrokowego u obserwatora normalnego. Strumień świetlny mierzony jest w lumenach [lm]. Wartość znamionowa strumienia świetlnego jest podstawowym parametrem źródeł światła, który można znaleźć w katalogu (często też na opakowaniu). Rozchodzenie się strumienia świetlnego z oprawy w danym kierunku przestrzeni charakteryzuje światłość (symbol I), tzn. im większą ilość strumienia świetlnego wysyła oprawa w danym kierunku (w dany kąt bryłowy) tym większa jest światłość oprawy w tym kierunku. Jednostką światłości, która jest jednostką podstawową (definiowaną umownie) w układzie SI, jest kandela [cd].

Bryła fotometryczna światłości to bryła utworzona przez wektory światłości, których początek umieszczony jest w umownym środku źródła światła (rys. 1)

Rys. 1. Bryła fotometryczna światłości żarówki (z bańką przezroczystą)

Rozsył światłości oprawy jest jej podstawowym parametrem zawartym w katalogu. W ogólnym przypadku są to stabelaryzowane wartości światłości w wybranych kierunkach. W przypadku opraw obrotowo-symetrycznych wystarczy przedstawić krzywą światłości I_ oprawy w jednej płaszczyźnie (zawierającej oś symetrii oprawy), jako funkcję kąta wypromieniowania  (rys.2). Na podstawie krzywej światłości można określić kąt połówkowy γ rozsyłu strumienia świetlnego, tzn. kąt liczony od osi do kierunku, w którym wartość światłości jest równa połowie wartości maksymalnej (rys. 2). Często kąt połówkowy mylony jest z użytecznym kątem rozwarcia, tzn. kątem pomiędzy kierunkami, w których światłości jest równa połowie wartości maksymalnej. Należy zwracać na to uwagę, gdyż stosowanie przez producentów różnych oznaczeń może prowadzić do późniejszych błędów (dwukrotnych!). W przypadku żarówek halogenowych z reflektorem na opakowaniu podawany jest użyteczny kąt rozwarcia.

Rys. 2. Rozsyłu światłości oprawy obrotowo-symetrycznej przedstawiony w układzie biegunowym

W celu umożliwienia porównywania parametrów świetlnych opraw o różnych typach i mocach źródeł światła w katalogach krzywa światłości przedstawiona jest jako funkcja I'_ [cd/klm] światłości względnej przeliczonej względem wyrażonego w kilolumenach strumienia świetlnego _z zamontowanych w oprawie źródeł światła. Zatem światłości I_ [cd] oprawy oblicza się na podstawie katalogowej wartości światłości względnej I'_ [cd/klm] mnożąc ją przez wyrażony w kilolumenach katalogowy strumień świetlny _z [1000 lm = klm] zainstalowanych w oprawie źródeł światła.

Rys. 3. Kosinusowy rozsył światłości: a) wykres biegunowy, b) wykres prostokątny

W technice świetlnej wykresy światłości przedstawia się zazwyczaj w układzie biegunowym (rys. 3a), a nie jak zwyczajowo w matematyce w układzie prostokątnym (rys. 3b). Układ biegunowy lepiej obrazuje rzeczywiste parametry oprawy, gdyż powstaje przy założeniu, że kierunek  = 0° oznacza kierunek osiowy oprawy zawieszonej na suficie świecącej do dołu, a promienie wychodzą ze środka oprawy (układu) w różnych kierunkach. Należy jednak zdawać sobie sprawę, że ta sama funkcja przedstawiona w obu układach będzie miała różny wygląd, czego przykładem jest przedstawiona na rysunkach 3 funkcja kosinusowa. Funkcja ta odpowiada w technice świetlnej bryle fotometrycznej światłości powierzchni równomiernie rozpraszającej lub też krzywej światłości świetlówki w płaszczyźnie zawierającej jej oś (rys. 3). W obu układach różnie odczytuje się współrzędne punktów, co na rysunkach 3 przedstawiają linie przerywane pomagające określić współrzędne tego samego punktu P. W układzie biegunowym nie występują ujemne wartości kątów  (lewa część wykresu przedstawia krzywą światłości w płaszczyźnie dopełniającej prawą część do kąta półpełnego).

Prawo odwrotności kwadratów odległości

Do oceny jakości oświetlenia powierzchni płaskiej służy natężenie oświetlenia E (jednostka luks - [lx]). Zależność pomiędzy światłością I_α oprawy w kierunku  a natężeniem oświetlenia E_ na powierzchni w tym kierunku (rys. 4) opisuje wzór:

. (1)

Zależność ta nazywa się prawem odwrotności kwadratów odległości lub fotometrycznym prawem odległości, które mówi, że natężenie oświetlenia E_ [lx] w danym punkcie powierzchni jest wprost proporcjonalne do światłości I_ [cd] w kierunku tego punktu oraz kosinusa kąta  padania światła (zawartym między kierunkiem światłości a normalną do powierzchni), a odwrotnie proporcjonalne do kwadratu odległości l_ [m] tego elementu od oprawy. Fotometryczne prawo odległości jest słuszne, gdy odległość l_ jest co najmniej 5 razy większa niż największy wymiar oprawy.

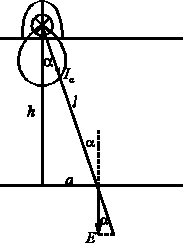
Rys. 4. Wyznaczanie natężenia oświetlenia na podstawie krzywej światłości oprawy

2. Cel i zakres ćwiczenia laboratoryjnego

Obliczenie metodą punktową, zgodnie z prawem odwrotności kwadratów, rozkładu natężenia oświetlenia na powierzchni roboczej oraz weryfikacja pomiarowa wyników obliczeniowych. Zapoznanie się z parametrami dostępnych handlowo reflektorowych żarówek halogenowych

3. Metodyka badań

W ćwiczeniu zastosowana zostanie niskonapięciowa żarówka halogenowa z reflektorem.

• Wskazane źródło światła z odbłyśnikiem umieścić poziomo nad powierzchnią roboczą w odległości h (odległość od źródła światła do powierzchni pomiarowej głowicy luksomierza) wskazanej przez prowadzącego (rys. 4).

• Znaleźć w katalogu parametry świetlne badanego źródła światła.

• Wyznaczyć teoretycznie wartości natężenia oświetlenia w punktach wskazanych przez prowadzącego (rys 4).

• Zmierzyć luksomierzem wartości natężenia oświetlenia na powierzchni roboczej w równomiernie rozłożonych punktach na prostej przechodzącej przez środek plamy świetlnej (rys. 4. - a = const).

• Wyznaczyć krzywą światłości wypełniając tabelkę (odległość l i kąt  wyznaczyć z zależności geometrycznych (rys. 4), a wartość światłości I_ z (1) po przekształceniu).

a	E	l		I
[m]	[lx]	[m]	[Ⴐ]	[cd]

• Wykreślić krzywą światłości [cd] żarówki w układzie biegunowym.

• Wyznaczyć użyteczny kąt rozwarcia badanego źródła światła.

• Porównać otrzymane wyniki z danymi katalogowymi źródła światła i przeanalizować wartości i źródła błędów.

• Badania powtórzyć przy innej wysokości umieszczenia żarówki nad powierzchnią roboczą.

4. Wymagania BHP

Wymagania BHP są zgodne z ogólnym regulaminem obowiązującym w laboratorium z przedmiotu: “Technika świetlna”.

5. Sprawozdanie

Sprawozdanie powinno zawierać: cel i zakres ćwiczenia, opis stanowiska badawczego z uwzględnieniem użytych przyrządów pomiarowych i urządzeń, przebieg realizacji ćwiczenia, zestawienie i analizę wyników badań, wnioski.

6. Pytania kontrolne

• Światłość, bryła fotometryczna światłości, krzywa światłości

• Kąt połówkowy i użyteczny kąt rozwarcia

• Dane katalogowe światłości względnej, a światłość oprawy

• Wykres funkcji kosinusowej w układzie biegunowym

• Natężenie oświetlenia

• Prawo odwrotności kwadratów odległości

7. Literatura

1. Żagan W.: Podstawy techniki świetlnej, Oficyna Wyd. Politechniki Warszawskiej, Warszawa 2005

2. Czyżewski D., Zalewski S.: Laboratorium fotometrii i kolorymetrii, Oficyna Wyd. Politechniki Warszawskiej, Warszawa 2007

2

---