Temat: Analiza statystyczna - miary tendencji centralnej
Celem kompletnej analizy statystycznej badanego zjawiska jest dojście do pewnego rodzaju uogólnień dotyczących tego zjawiska.
Średnia arytmetyczna:
średnia arytmetyczna zwykła (prosta)
jeżeli dane przedstawione są w postaci indywidualnego szeregu wartości cechy to średnią obliczamy według wzoru:
![]()
gdzie:
xi - wartość cechy statystycznej
N - liczebność zbiorowości
Przykład:
Uczeń dostał następujące oceny: 5, 6, 5, 4, 3 oblicz średnią:
![]()
Odp.: Średnia ocen wynosi 4,6
średnia arytmetyczna ważona
jeżeli informacje dotyczące wartości cech są podane w formie szeregu statystycznego rozdzielczego:
z cechą mierzalną ze zmiennością skokową stosuje się wzór:
![]()
gdzie:
ni - liczebność cząstkowa
Przykład:
oceny (xi) |
ilość (ni) |
xi*ni |
1 |
4 |
4 |
2 |
10 |
20 |
3 |
8 |
24 |
4 |
2 |
8 |
5 |
3 |
15 |
6 |
1 |
6 |
Razem |
28 |
77 |
![]()
Odp.: średnia otrzymanych ocen wynosi 2,75
gdzie zastosowano rozpiętość przedziałów klasowych średnia oblicza się ze wzoru:
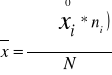
gdzie:
![]()
- średnia przedziału klasowego
Przykład:
oceny (xi) |
ilość (ni) |
|
1 - 2 |
5 |
1,5 * 5 = 7,5 |
3 - 4 |
10 |
3,5 * 10 = 35 |
5 - 6 |
3 |
5,5 * 3 = 16,5 |
Razem |
18 |
59 |
![]()
= (1+2):2= 1,5 ![]()
![]()
Dominanta - jest to wartość cechy, która najczęściej występuje w badanej zbiorowości statystycznej. Nazywa się ją również wartością modalną (moda)
wskazuje się, kiedy dane przedstawione są w postaci indywidualnego szeregu wartości oraz szeregu statystycznego z cechą mierzalna ze zmiennością skokowa. Jest to taka wartość zmiennej, która w danym szeregu występuje najczęściej
Przykład:
Indywidualny szereg wartości: 5, 6, 5, 4, 3
Dx = 5
Szereg statystyczny z zmiennością skokową:
oblicza się, gdy dane przedstawione są w postaci szeregu statystycznego z cechą mierzalna ze zmiennością ciągłą ( gdy są przedziały klasowe).
Mediana - jest to wartość środkowa, dzieląca zbiorowość na dwie równe części.
szereg uporządkowany indywidualny o nieparzystej liczbie jednostek
szereg uporządkowany indywidualny o parzystej liczbie jednostek
szereg statystyczny z cechą mierzalną z zmiennością skokową.
szereg statystyczny z cecha mierzalną z zmiennością ciągłą (wartości cech są ujęte w przedziałach klasowych)
Wskaźnik struktury - wskaźnik udziału liczebności cząstkowej do liczebności globalnej.
Ułamkowe wskaźniki struktury
Wskaźnik procentowy
Wskaźnik natężenia - są to wielkości stosunkowe, wyrażające kształtowanie się wielkości jednego zjawiska na tle innego, logicznie z nim związanego
…
…
…
oceny (xi) |
ilość (ni) |
1 |
4 |
2 |
10 |
3 |
8 |
4 |
2 |
5 |
3 |
6 |
1 |
Razem |
28 |
Dx = 2
W przedziale gdzie jest największa liczba jednostek obliczamy dominantę.
![]()
gdzie:
xo - dolna granica przedziału klasowego, w którym występuje dominanta
L - rozpiętość przedziału klasowego
n - liczebność przedziału dominanty
n-1 - liczebność przedziału poprzedzająca dominantę (jak niema żadnego wcześniej to wpisujemy 0)
n1 - liczebność przedziału występująca po dominancie
Przykład:
oceny (xi) |
ilość (ni) |
1 - 2 |
5 |
3 - 4 |
10 |
5 - 6 |
3 |
Razem |
18 |
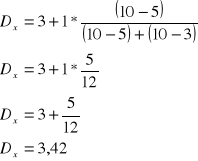
Wynik musi się mieścić w przedziale szeregowym dominanty.
Wyznaczanie w poszczególnych szeregach statystycznych:
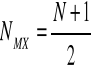
Przykład:
Oceny ucznia:
1, 2, 3, 5, 4, 6, 4, 3, 3, - szereg nieuporządkowany
1, 2, 3, 3, 3, 4, 4, 5, 6, - szereg uporządkowany
![]()
Mx = 3
Odp.: Wartością środkowa jest 3, co oznacza ze połowa jednostek ma wartość większą niż 3, a połowa mniejsza niż 3.
![]()
![]()
Z wartości tych wyrazów obliczamy średnią arytmetyczną, która jest medianą
Przykład:
Oceny ucznia:
1, 2, 2, 3, 3, 4, 4, 5, 6, 6,
![]()
![]()
Średnia arytmetyczna:
![]()
Należy utworzyć szereg skumulowany i ustalić numer jednostki środkowej
oceny (xi) |
ilość (ni) |
ilość skumulowana |
1 |
8 |
8 |
2 |
6 |
14 (8+6) |
3 |
12 |
26 (14+12) |
4 |
5 |
31 (26+5) |
5 |
1 |
32 (31+1) |
6 |
1 |
33 (32+1) |
Razem |
33 |
|
Ustalamy czy liczebność zbiorowości (N) jest liczbą parzysta czy nieparzystą.
![]()
W kolumnie skumulowanej wybieramy przedział w której znajduje się pozycja mediany
![]()
![]()
gdzie:
xoMX - górna wartość przedziału klasowego w którym znajduje się mediana
L - rozpiętość przedziału klasowego
SSMX-1 - wartość szeregu skumulowana poprzedzająca medianę
Przykład:
oceny (xi) |
ilość (ni) |
szereg skumulowany |
1 - 2 |
5 |
5 |
3 - 4 |
10 |
15 |
5 - 6 |
3 |
18 |
Razem |
18 |
|
18 - liczba parzysta
![]()
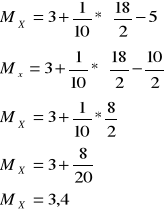
Odp.:
Struktura zbiorowości określona jest przez podział badanej zbiorowości statystycznej na grupy jednostek różniących się od siebie wartościami poszczególnych cech.
Wskaźnik struktury możemy obliczyć jako:
![]()
gdzie:
ni - liczebność poszczególnych części danej zbiorowości
N - liczebność całej zbiorowości statystycznej
![]()
Najczęściej spotykanym współczynnikiem natężenia są np. gęstość zaludnienia, liczba urodzeń małżeństw, wskaźnik umieralności, wskaźnik wydajności pracy, produkcja energii elektrycznej w Kw. Na 1 mieszkańca.
![]()
gdzie:
N1 - wielkość jednej zbiorowości
N2 - wielkość drugiej zbiorowość
ZADANIA
Zadanie 1
Oblicz lub wskaż średnią arytmetyczną, dominantę i medianę oraz zinterpretuj wyniki poniższych danych.
Powierzchnia sklepu w m2: 20, 80, 40, 40, 20, 15, 20, 18, 15, 20, 80, 18, 20
powierzchnia w m2 (xi) |
ilość (ni) |
20 |
5 |
40 |
15 |
60 |
5 |
Razem |
25 |
powierzchnia w m2 (xi) |
ilość (ni) |
(20 - 40> |
10 |
(40 - 60> |
20 |
(60 - 80> |
8 |
Razem |
38 |
Rozwiązanie:
Szereg:
nieuporządkowany: 20, 80, 40, 40, 20, 15, 20, 18, 15, 20, 80, 18, 20
uporządkowany:15, 15, 18, 18, 20, 20, 20, 20, 20, 40, 40, 80, 80
średnia arytmetyczna:
![]()
Odp.: Średnia powierzchnia sklepów wynosi 31,23m2
dominanta:
Dx = 20m2
Odp.: Sklepy maja najczęściej powierzchnię 20m2
mediana:
![]()
Odp.: Połowa sklepów ma mniejsza powierzchnię niż 20m2, a druga połowa sklepów badanych ma większą powierzchnię niż 20m2
B.
powierzchnia w m2 (xi) |
ilość (ni) |
xi * ni |
szereg skumulowany |
20 |
5 |
100 |
5 |
40 |
15 |
600 |
20 |
60 |
5 |
300 |
25 |
Razem |
25 |
1000 |
|
średnia arytmetyczna:
![]()
Odp.: Przeciętna powierzchnia sklepów wynosi 40m2
dominanta:
Dx= 40
Odp.: Najwięcej jest sklepów o powierzchni 40m2
mediana:
![]()
Mx= 40
Odp.: Połowa sklepów ma powierzchnie mniejsza od 40m2, a druga większą.
C.
powierzchnia w m2 (xi) |
ilość (ni) |
|
|
szereg skumulowany |
(20 - 40> |
10 |
30 |
300 |
10 |
(40 - 60> |
20 |
50 |
1000 |
30 |
(60 - 80> |
8 |
70 |
560 |
38 |
Razem |
38 |
|
1860 |
|
średnia arytmetyczna:
![]()
Odp.: Średnia powierzchnia sklepów wynosi 48,95m2
dominanta:
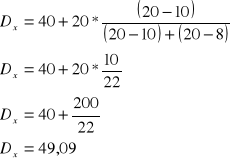
Odp.: Najwięcej sklepów ma powierzchnię 49m2
mediana:
![]()
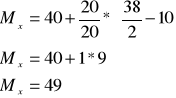
Odp.: Połowa sklepów ma powierzchnie większą od 49m2, a druga połowa sklepów ma mniejsza powierzchnię niż 49m2.
Wyszukiwarka
Podobne podstrony:
statystyka, ekonomika przewdsiebiorstw
Zadania statystyka i ekonometria
Przyk-adowe zadania na egzamin ze statystyki, ekonomia, 2 rok, statystyki test
Rola i zadania statystyki w administracji, EKONOMIA
Zadanie370, Informatyka i Ekonometria 2 rok, badania operacyjne, sciagniete z internetu
Zadanie Domowe 4, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy
zadania dodatkowe, Ekonomia- studia, Finanse publiczne i rynki finansowe
dane skorelowane zadania, statystyka, statystyka
Zadania statystyka 2
Ekonometria - zadania transportowe, Ekonometria
zadania statystyka[1]
Zadania statystyka
statystyka zadanie, statystyka i demografia-Hnatyszyn-Dzikowska ćwiczenia
zadania z mikroekonomi, Ekonomia, ekonomia
statystyka i ekonometria XDTCVH3BH3DIFXWBHH22BEIUDA5ESVRZ25P2UZY
statystyka-5-zadania, Statystyka, zadania
więcej podobnych podstron