106 nr cwicz	15-04 2001 data	Tomasz Golon imię i nazwisko	elektryczny wydział	II semestr	E-9 grupa
mgr J. Gutek prowadzący		przygotowanie	wykonanie	opracowanie	ocena ostateczna

Temat: Wyznaczanie współczynnika przewodnictwa cieplnego metali.

Wstęp teoretyczny

Przewodnictwem cieplnym nazywamy przekazywanie energii kinetycznej jednych drobin do drugich w wyniku ich zderzeń.

Strumieniem ciepła
przepływającego przez przekrój pręta określamy poniższym równaniem:

Czyli jako stosunek ilości ciepła do czasu.

Zgodnie z podstawowym prawem przewodnictwa cieplnego możemy zapisać:

gdzie:
nazywamy współczynnikiem przewodnictwa cieplnego, mierzymy go
;

Przy rozpatrywaniu pręta dokładnie izolowanego o stałym przekroju możemy korzystać z równania:

Możemy więc łatwo zauważyć że, gdy
jest duże, wówczas chcąc utrzymać stałą różnicę temperatur
musimy dostarczyć duży strumień ciepła. Natomiast gdy
jest małe to przekazywanie ciepła do zimnego końca jest powolne. W tym przypadku aby podtrzymać stałą różnicę temperatur wystarczy nam mały strumień dostarczanego ciepła.

Rozkład temperatury wzdłuż takiego (izolowanego) pręta otrzymujemy stosując poniższy wzór:

W przypadku gdy powierzchnia boczna pręta nie jest izolowana cieplnie, przepływający przez kolejne powierzchnie strumień jest coraz mniejszy. Dzieje się tak ponieważ część ciepła ucieka do otoczenia. Biorąc pod uwagę prawo ostygania tz., że strumień ciepła przez ściany boczne jest proporcjonalny do różnicy temperatur między danym punktem a otoczeniem możemy otrzymać następujące równanie opisujące rozkład temperatury w postaci:

,

gdzie: h jest stałą charakteryzującą pręt i ośrodek zewnętrzny.

Ciała, których przewodnictwo elektryczne jest duże są dobrymi przewodnikami ciepła. Potwierdza to prawo Wiedemanna-Franza które mówi, że stosunek przewodnictwa cieplnego
do przewodnictwa elektrycznego
jest proporcjonalny do temperatury i nie zależy on od rodzaju ciała

.

W celu wyznaczenia współczynnika cieplnego metali stosujemy układ pomiarowy przedstawiony poniżej:

Jak można zauważyć na powyższym rysunku jeden koniec pręta umieszczamy w grzejniku a drugi w wodzie z lodem. Pręt ten jest izolowany cieplnie od otoczenia. Pomiaru temperatury dokonujemy w kilku miejscach. Strumień cieplny który przepływa przez pręt pochodzi od grzejnika. Jego wielkość zależy od wydajności grzejnika:

ponieważ nie całkowity strumień (będący mocą przepływającego przez niego prądu) zostanie przekazany prętowi.

Schemat doświadczenia

• Najpierw mierzymy średnicę pręta

• Następnie łączymy obwód grzejnika oraz termopar według rysunku. Naczynie wypełniamy wodą z lodem

• Włączamy grzejnik i czekamy na ustalenie się temperatury

• Przy ustalonym przepływie mierzymy napięcie i prąd grzejnika, oraz temperaturę wszystkich punktów pomiarowych badanych prętów

• Sporządzamy wykres zależności temperatury w pręcie od odległości

• Z nachylenia wykresu dla stanu równowagi znajdujemy gradient temperatury (dt/dx) stosując regresję liniową

• Obliczamy współczynnik przewodnictwa cieplnego

• Powyższe obliczenia stosujemy dla jeszcze 2 innych wartości napięcia grzejnika

Pomiary i obliczenia:

Promień rurki - r [mm]		Sprawność grzejnika - η		Odległość między punktami pomiarów X [mm]
Aluminiowej	Mosiężnej	Aluminiowego	Mosiężnego
10 0,1	10 0,1	0,52 0,01	0,24 0,01	50 2

Tabelka z pomiarami temperatury w stanie ustalonym.

Napięcie i natężenie	50 V, 135 mA		60 V, 165 mA		65 V, 179 mA
x [mm]	Temperatura ^oC		Temperatura ^oC		Temperatura ^oC
		aluminium	mosiądz	aluminium	mosiądz	aluminium	mosiądz
0	23,7	23,9	26,8	26,7	29,9	30,3
50	21,9	21,1	24,5	23,3	27,3	26,4
100	19,2	18,8	21,4	20,7	24	23,3
150	16,6	15,9	18,2	17,6	20,7	20,1
200	14,1	12,8	15,2	14,7	17,7	16,9

Strumień ciepła:

Nr pomiaru Rurka	1	2	3
Mosiężna	1620	2376	2792
Aluminiowa	3510	5146	6050

Przekrój prętów wynosi:

A = 314,159 [mm]

Gradient temperatury

Nr pomiaru	aluminium	mosiądz
1	0,049	0,058
2	0,059	0,059
3	0,062	0,066

Pomiar	α
		Aluminium	Mosiądz
1	0,105237235	0,1926325
2	0,128187276	0,2776312
3	0,14334225	0,2917843

Współczynnik przewodnictwa cieplnego

Używane wzory:

Aby obliczyć współczynnik przewodnictwa cieplnego należy skorzystać z poniższego wzoru:

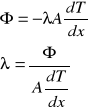
Gdzie
- jest gradientem temperatury, możemy go odczytać z współczynników kierunkowych prostych wykreślających zależność temperatury w pręcie od odległości

Przekrój pręta - A obliczymy ze wzoru:

Natomiast Φ obliczamy ze wzoru:

Dyskusja błędów:

Błąd A obliczamy następująco:

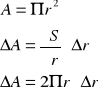
gdzie: r=0,1mm

Zatem A = 6,28

Błąd strumienia obliczamy za pomocą różniczki zupełnej:

gdzie: ΔU=0,5V; ΔI=0,0005A

Więc odpowiednio:

	Aluminiowa	Mosiężna	Aluminiowa	Mosiężna	Aluminiowa	Mosiężna
[W]	13	6	15,6	7,2	16,9	7,8

Błąd dla współczynnika przewodnictwa cieplnego obliczamy stosując różniczkę zupełną, więc:

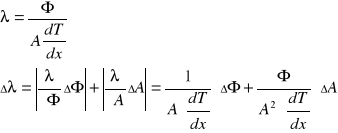
Otrzymujemy więc:

[W/(mK)]	Nr pom.	Mosiądz	Aluminium
		1	175,736183	450,6976
		2	253,291497	548,5854
		3	266,039215	613,6741

Przykład obliczeń:

Przykład obliczenia błędu współczynnika przewodnictwa cieplnego dla 1 pomiaru - mosiądzu:

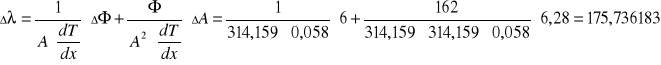
Wnioski:

Jak możemy zauważyć na wykresie aluminium wolniej się ochładza niż mosiądzu. Błędy w wynikach mogą być spowodowane niedokładnością przyrządów pomiarowych oraz tym, że trudno było dokładnie określić moment ustabilizowania się przepływu strumienia.

Wykres zależności temperatury w pręcie od odległości

---