Podstawowe pojęcia i wzory
III. ANALIZA MATEMATYCZNA
GRANICA I CIĄGŁOŚĆ FUNKCJI
GRANICA FUNKCJI
Definicja Heinego granicy funkcji (ciągowa)
Dla funkcji ![]()
i ![]()
liczba rzeczywista q jest granicą funkcji f w x0,
/symbolicznie: „![]()
” /
wtedy, gdy dla każdego ciągu![]()
,takiego, że:![]()
, to ![]()
Inaczej:
![]()
Definicja Cauchy'ego granicy funkcji
Liczba q jest granicą funkcji f w x0 wtedy i tylko wtedy, gdy:
dla każdej liczby rzeczywistej ![]()
> 0 istnieje liczba rzeczywista ![]()
> 0 taka, że
dla każdego ![]()
:
jeśli ![]()
![]()
, to ![]()
Inaczej:
![]()
f(x)
![]()
![]()
![]()
![]()
x
f(x)
![]()
x
Definicja 1
Funkcja f ma w punkcie x0 granicę ![]()
, jeżeli dla dowolnej liczby rzeczywistej ![]()
istnieje taka liczba ![]()
(dobrana do ε), że dla wszystkich ![]()
spełniających warunek ![]()
zachodzi nierówność ![]()
co zapisujemy:
![]()
Analogicznie definiujemy granicę równą ![]()
.
Definicja 2
Funkcja f ma granicę równą g przy x zmierzającym do ![]()
jeżeli dla dowolnej liczby rzeczywistej ![]()
istnieje P<0 takie, że dla wszystkich x spełniających warunek x<P zachodzi nierówność ![]()
, co zapisujemy:
![]()
Analogicznie zdefiniujemy granicę funkcji przy x zmierzającym do ![]()
.
Twierdzenie 1
Jeżeli ![]()
i ![]()
, to
![]()
![]()
![]()
![]()
przy dodatkowym założeniu, że ![]()
![]()
Twierdzenie 2
Jeżeli ![]()
i ![]()
, to
![]()
![]()
jeżeli ![]()
lub ![]()
gdy ![]()
![]()
Analogicznie będziemy liczyć granicę, w przypadku, gdy ![]()
.
Twierdzenie 3
Jeżeli ![]()
i ![]()
, to
![]()
![]()
jeżeli ![]()
lub ![]()
, gdy ![]()
![]()
Twierdzenie 4
Jeżeli ![]()
i ![]()
oraz ![]()
, to
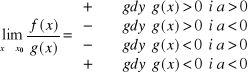
Twierdzenie 5 (o trzech funkcjach)
Jeżeli ![]()
oraz ![]()
w pewnym otoczeniu punktu x0
to ![]()
Definicja 3
Liczbę g nazywamy lewostronną [prawostronną] granicą funkcji w punkcie x0, jeżeli dla dowolnej liczby rzeczywistej ![]()
istnieje taka liczba ![]()
(dobrana do ε), że dla wszystkich ![]()
spełniających warunek ![]()
[![]()
] zachodzi nierówność ![]()
.
Zatem możemy to zapisać symbolicznie:
![]()
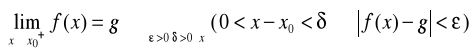
Przykłady ważniejszych granic
Rozważmy przypadki:
n = m
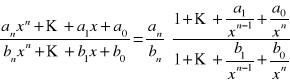
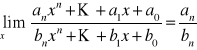
.
n < m
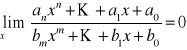
c)n > m
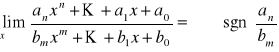
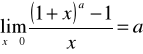
;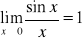
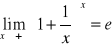
CIĄGŁOŚĆ FUNKCJI
Definicja 4
Funkcja rzeczywista f jest ciągła w punkcie x0 wtedy i tylko wtedy gdy:
![]()
.
Korzystając z dwóch definicji granicy funkcji otrzymujemy dwie równoważne definicje ciągłości.
Definicja Heinego ciągłości funkcji
Funkcja rzeczywista f jest ciągła w punkcie x0 wtedy i tylko wtedy, gdy:
![]()
Definicja Cauchy'ego ciągłości funkcji
Funkcja rzeczywista f jest ciągła w punkcie x0 wtedy i tylko wtedy, gdy
![]()
Y
y=f(x)
![]()
![]()
![]()
![]()
![]()
![]()
X
Twierdzenie 6
Suma, różnica oraz iloczyn funkcji ciągłych
w pewnym punkcie jest funkcją ciągłą w tym punkcie.
Jeżeli funkcje
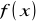
i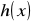
są ciągłe w punkcie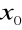
i ![]()
, to iloraz ![]()
/ ![]()
jest także funkcją ciągłą w tym punkcie.
Funkcja stała
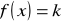
oraz funkcja tożsamościowa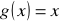
są ciągłe w każdym punkcie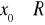
Wniosek
Każdy wielomian W![]()
jest funkcją ciągłą w dowolnym punkcie ![]()
.
Funkcja wymierna jest więc ciągła w każdym punkcie swej dziedziny naturalnej, którą jest zbiór R z wyjątkiem pierwiastków wielomianu znajdującego się w mianowniku.
Funkcje trygonometryczne, funkcja wykładnicza oraz logarytmiczna są ciągłe w swoich dziedzinach.
Definicja 5
Funkcja jest ciągła w zbiorze, jeżeli jest ciągła w każdym punkcie tego zbioru.
Definicja 6
Funkcja rzeczywista f jest prawostronnie ciągła w punkcie x0 jeżeli spełniony jest warunek
![]()
gdzie ![]()
oznacza granicę prawostronną funkcji f w punkcie x0.
Funkcja rzeczywista f jest lewostronnie ciągła w punkcie x0 jeżeli spełniony jest warunek
![]()
.
gdzie ![]()
oznacza granicę lewostronną funkcji f w punkcie x0.
Twierdzenie 7
Jeżeli funkcja ![]()
jest ciągła w punkcie ![]()
, to jest w tym punkcie lewo- i prawostronnie ciągła, a także na odwrót.
Definicja 7
Funkcja rzeczywista f jest ciągła w przedziale domkniętym [a;b] jeżeli spełnia następujące warunki:
jest ciągła w przedziale
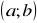
prawostronnie ciągła w punkcie a,
lewostronnie ciągła w punkcie b.
Definicja 8
Jeżeli funkcja ![]()
nie jest ciągła w punkcie ![]()
, to ![]()
nazywamy punktem nieciągłości tej funkcji.
Rodzaje nieciągłości
Nieciągłość pierwszego rodzaju - funkcja ma obydwie granice jednostronne właściwe (skończone).
Nieciągłość drugiego rodzaju - pozostałe przypadki
Definicja 9
Skok funkcji f w punkcie ![]()
definiujemy jako:
![]()
.
WŁASNOŚCI FUNKCJI CIĄGŁYCH
Twierdzenie o ciągłości funkcji odwrotnej
Funkcja odwrotna do funkcji ciągłej i rosnącej (malejącej) jest ciągła i rosnąca (malejąca).
Twierdzenie o ciągłości funkcji złożonej
Jeżeli funkcja ![]()
jest ciągła w punkcie ![]()
i funkcja ![]()
jest ciągła w punkcie ![]()
, to funkcja złożona ![]()
jest ciągła w punkcie ![]()
.
POCHODNA FUNKCJI
Definicja 10
Otoczeniem otwartym punktu a o promieniu ε nazywamy dowolny przedział postaci (a- ε, a+ε)
Sąsiedztwem punktu a o promieniu δ nazywamy zbiór (a-δ, a+δ)-{a}
Definicja 11
Punkt x0 nazywamy punktem skupienia zbioru X, jeżeli każde sąsiedztwo tego punktu ma niepuste przecięcie ze zbiorem X.
Uwaga Punkt skupienia nie musi należeć do zbioru X.
Załóżmy, że funkcja ![]()
jest określona w przedziale ![]()
i ![]()
jest ustalonym punktem tego przedziału. Niech ![]()
oznacza taką liczbę różną od zera, że ![]()
Z przyjętych założeń wynika, że ![]()
może być zarówno liczbą dodatnią, jak i ujemną. Rozpatrzmy teraz funkcję ![]()
, która liczbie ![]()
przyporządkowuje liczbę ![]()
Zatem
![]()
Wobec tego ![]()
jest ilorazem różnicowym funkcji ![]()
odpowiadającym przyrostowi argumentu ![]()
o liczbę ![]()
Interesować nas będzie granica ![]()
a więc granica ![]()
Definicja 12
Jeśli funkcja ![]()
jest określona w przedziale ![]()
![]()
i istnieje skończona granica ![]()
to granicę tę nazywamy pochodną funkcji ![]()
w punkcie ![]()
i oznaczamy symbolem ![]()
O funkcji ![]()
, która ma pochodną w punkcie ![]()
mówimy również, że jest różniczkowalna w tym punkcie. Jeżeli funkcja ![]()
ma pochodną w każdym punkcie przedziału ![]()
to funkcję ![]()
nazywamy różniczkowalną w przedziale ![]()
Twierdzenie 8
Pochodna funkcji f w punkcie ![]()
jest współczynnikiem kierunkowym stycznej do wykresu funkcji f, poprowadzonej w punkcie ![]()
.
Definicja 13
Styczną do wykresu funkcji f, poprowadzoną w punkcie ![]()
nazywać będziemy prostą o równaniu
![]()
.
Definicja 14
Pochodną funkcji f nazywać będziemy funkcję, która każdemu argumentowi ![]()
funkcji f, w którym istnieje pochodna tej funkcji, przyporządkowuje wartość pochodnej funkcji w tym punkcie , tzn. liczbę ![]()
.
Twierdzenie 9
Jeżeli funkcja f posiada pochodną w punkcie ![]()
, to jest w tym punkcie ciągła.
Twierdzenie 10
Jeżeli funkcje f, g posiadają pochodne w punkcie x, to funkcje ![]()
posiadają pochodne w tym punkcie oraz zachodzą równości
![]()
![]()
![]()
Jeżeli dodatkowo ![]()
, to funkcja ![]()
posiada pochodną w punkcie x oraz
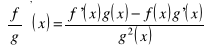
Twierdzenie 11
Jeżeli funkcja ![]()
posiada pochodną w punkcie ![]()
, a funkcja ![]()
posiada pochodną w punkcie ![]()
, to funkcja złożona ![]()
posiada pochodną w punkcie ![]()
oraz
![]()
.
Twierdzenie 12
Jeżeli funkcja f jest monotoniczna i ciągła na przedziale ![]()
oraz posiada pochodną w punkcie ![]()
, różną od zera ![]()
, to funkcja odwrotna ![]()
posiada pochodną w punkcie ![]()
oraz
![]()
Definicja 15
Różniczką funkcji f w punkcie ![]()
dla przyrostu ![]()
nazywamy wyrażenie
![]()
Tablica pochodnych funkcji elementarnych:
Pochodne |
|
Zakres zmienności x |
|
|
|
|
|
W zależności od |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EKSTREMA LOKALNE FUNKCJI, ASYMPTOTY FUNKCJI.
Definicja 16
Mówimy, że funkcja f osiąga w punkcie ![]()
maksimum lokalne (minimum lokalne), jeżeli istnieje takie otoczenie U punktu ![]()
, że dla każdego punktu ![]()
spełniona jest nierówność
![]()
Liczbę ![]()
nazywamy wówczas odpowiednio maksimum lokalnym (minimum lokalnym).
Twierdzenie 13 (Warunek konieczny istnienia ekstremum funkcji różniczkowalnej)
Jeżeli funkcja f jest różniczkowalna w punkcie ![]()
i posiada w punkcie ![]()
ekstremum, to ![]()
.
Uwaga. Warunek ten nie jest dostateczny.
Twierdzenie 14 (Warunek dostateczny istnienia ekstremum lokalnego)
Jeżeli funkcja f jest ciągła w pewnym otoczeniu U punktu ![]()
, jest różniczkowalna w pewnym sąsiedztwie tego punktu oraz dla ![]()
zachodzi jeden z warunków:
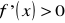
dla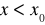
i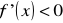
dla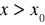
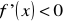
dla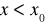
i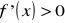
dla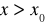
,
to funkcja f osiąga w punkcie ![]()
odpowiednio maksimum (minimum lokalne).
Definicja 17
Pochodną drugiego rzędu (drugą pochodną) funkcji f nazywamy pochodną pochodnej tej funkcji
![]()
Analogicznie określamy pochodne wyższych rzędów.
Definicja 18
Mówimy, że funkcja f jest wypukła (wklęsła) na pewnym zbiorze A, jeżeli dla dowolnych ![]()
punkty wykresu funkcji f w przedziale ![]()
leżą poniżej (powyżej) siecznej, przechodzącej przez punkty ![]()
oraz ![]()
.
Uwaga. Jeżeli funkcja f różniczkowalna na zbiorze A, to wypukłość (wklęsłość) można zastąpić warunkiem, by w każdym punkcie x zbioru A wykres funkcji f leżał nad (pod) styczną, poprowadzoną do wykresu tej funkcji w punkcie ![]()
Twierdzenie 15
Jeżeli funkcja f posiada na przedziale ![]()
ciągłe pochodne pierwszego i drugiego rzędu oraz ![]()
![]()
dla ![]()
, to funkcja f jest na tym przedziale wypukła (wklęsła).
Definicja 18
Mówimy, że punkt ![]()
jest punktem przegięcia wykresu funkcji f, jeżeli w pewnym lewostronnym sąsiedztwie punktu ![]()
funkcja f jest wklęsła, a w pewnym prawostronnym sąsiedztwie tego punktu jest wypukła lub na odwrót.
Twierdzenie 16 (Warunek konieczny istnienia punktu przegięcia funkcji różniczkowalnej)
Jeżeli funkcja f posiada w otoczeniu punktu ![]()
pochodne pierwszego i drugiego rzędu oraz punkt ![]()
jest punktem przegięcia wykresu funkcji f, to ![]()
.
Twierdzenie 17 (Warunek dostateczny istnienia punktu przegięcia)
Jeżeli funkcja f posiada w otoczeniu punktu ![]()
pochodne pierwszego i drugiego rzędu oraz
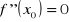
w lewostronnym sąsiedztwie punktu
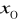
druga pochodna jest dodatnia, a w prawostronnym sąsiedztwie jest ujemna (lub na odwrót),
to punkt ![]()
jest punktem przegięcia krzywej ![]()
.
Definicja 19
Jeżeli ![]()
jest punktem skupienia dziedziny funkcji f oraz istnieje granica jednostronna ![]()
![]()
i jest niewłaściwa, to prostą ![]()
nazywamy asymptotą pionową lewostronną (prawostronną) funkcji f.
Definicja 20
Jeżeli funkcja f jest określona co najmniej w przedziale ![]()
![]()
oraz istnieje prosta o równaniu ![]()
taka, że ![]()
![]()
, to prostą ![]()
nazywamy asymptotą ukośną lewostronną (prawostronną) funkcji f.
W szczególnym przypadku, gdy ![]()
, asymptota ukośna jest asymptotą poziomą (ma to miejsce wtedy, gdy funkcja ta ma w ![]()
lub w ![]()
skończoną granicę).
Badanie przebiegu zmienności funkcji:
Dziedzina funkcji.
Granice funkcji na brzegu dziedziny.
Asymptoty funkcji.
Ekstrema i przedziały monotoniczności funkcji: pierwsza pochodna funkcji, jej miejsca zerowe i punkty nieróżniczkowalności, znak pierwszej pochodnej.
Wklęsłość i wypukłość funkcji oraz jej punkty przegięcia: pochodna drugiego rzędu, jej miejsca zerowe i znak.
Zebranie wyników w tabelce.
Narysowanie wykresu funkcji.
1
a- ε a a+ ε
a-δ a a+δ
Wyszukiwarka
Podobne podstrony:
WYKLAD ANALIZA MATEMATYCZNA
Analiza matematyczna, lista analiza 2008 6 szeregi
Analiza Matematyczna 1 Gewert Skoczylas zadania
Analiza Matematyczna Twierdzenia
Analiza matematyczna 1
Praca domowa 2a Analiza Matematyczna
Zadania z Analizy Matematycznej, Matematyka
zestaw9, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
Analiza matematycza opracowanie pytań
Kolos 3 Analiza matematyczna
analiza matematyczna 7
Analiza matematyczna 2 Przyklady i zadania
cw 13 Analiza Matematyczna (calki) id
Analiza matematyczna 1, tab
,analiza matematyczna 2, elemen Nieznany (2)
zestaw10, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
a2k, WTD, analiza matematyczna
CALY E -TRAPEZ, PWR, Analiza Matematczna
więcej podobnych podstron