Podział zadań tekstowych ze względu na strukturę:

- zadania poprawnie skonstruowane

- zadania z niedoborem danych

- zadania ze zbyt dużą liczbą danych niesprzecznych

- zadania z danymi wzajemnie sprzecznymi

- zadania otwarte

Podział zadań ze względu na złożoność konstrukcyjną:

- zadania proste

- zadania złożone łańcuchowo

- właściwe zadania złożone

Podział zadań ze względu na formę: statyczne i dynamiczne.

Układanie zadań tekstowych przez uczniów:

- układanie zadań analogicznych do danych z wykorzystaniem tych samych liczb lub działań

- układanie zadań z rozsypani

- układnie zadań do konkretnej sytuacji związanej z czynnościami

- zakładanie zadań do ilustracji

- układanie zadań do działań

- układanie zadań do sytuacji ogólnej, gdy trzeba wybrać pewne elementy (np. kupowanie z cennikiem)

- układanie zadań do schematu

Metoda „kruszenia” jest jedną z nowoczesnych metod rozwiązywania zadań tekstowych.

„Kruszenie w czasie rozwiązywania zadań oznacza modyfikowanie, zwiększanie lub zmniejszanie danych i ich wartości, zastępowanie danych innymi, zmianę miejsca danych, a także przekształcanie zadania, jego odwracanie, wprowadzanie nowych związków i zależności, uszczegóławianie lub uogólnianie zadania.”

Proces „kruszenia” rozpoczyna się zawsze od tzw. Zadania bazowego, które jest najczęściej złożone, otwarte, niestandardowe i nie zawiera pytań.

Dzieci najchętniej rozwiązują zadania, których treść związana jest z ich przeżyciami oraz odzwierciedla ich zainteresowania.

I. Na planszy, tablicy lub grafoskopie prezentujemy uczniom treść zadania bazowego:
Na uroczystość klasową przygotowano 6 małych stolików 4 - osobowych i 4 stoliki duże 8 - osobowe.

• Zadanie zostaje odczytane, wyjaśnione są niezrozumiałe słowa. Treść jest cały czas widoczna dla uczniów.

II. Układanie przez dzieci pytań szczegółowych:

• Polecenie dla uczniów: Pomyśl i powiedz, co można obliczyć na podstawie treści i danych liczbowych zadania bazowego. Ułóż odpowiednie pytanie.

• Motywowanie uczniów do pracy: Przyjmujemy każdy pomysł, nie ma pomysłów złych.

• Zapisywanie wszystkich pytań na tablicy bez oceny ich poprawności:

1. Ile osób usiądzie przy stolikach małych ?

2. Ile osób usiądzie przy stolikach dużych ?

3. Dla ilu osób przygotowano miejsca ?

4. Których stolików jest więcej i o ile ?

5. O ile mniej osób usiądzie przy stolikach małych ?

6. Ile było stolików małych?

7. O ile więcej osób usiądzie przy stoliku dużym ?

8. Ile jest wszystkich stolików ?

9. Których stolików jest więcej ?

10. Ile osób usiądzie przy 1 stoliku małym i 1 stoliku dużym razem?

11. Ile stolików 4 - osobowych można zrobić z 1 stolika 8 - osobowego ?

12. Ile stolików 4 - osobowych trzeba przygotować, aby posadzić przy nich wszystkie osoby siedzące przy dużych stolikach ?

III. Sprawdzenie sensowności i poprawności ułożonych pytań poprzez: ich analizę, układanie do nich działań i obliczanie wyników.

• Polecenie dla uczniów: Przeczytaj uważnie pytanie. Pomyśl, jak obliczyć niewiadomą zawartą w pytaniu. Zapisz działanie obok pytania.

• Motywowanie uczniów do pracy: Zastanów się, czy ułożone pytanie ma sens i logiczną odpowiedź.

• Zapisywanie przez uczniów działań matematycznych obok wcześniej ułożonych pytań.

1. 6 ? 4 = 24

2. 4 ? 8 = 32

3. 6 ? 4 + 4 ? 8 = 52

4. 6 - 4 = 2

5. 4 ? 8 - 6 ? 4 = 8

6. - ta liczba była podana w zadaniu - pytanie wymazujemy

7. 8 - 4 = 4

8. 6 + 4 = 10

9. - pytanie powtarza się - wymazujemy je

10. 4 + 8 = 12

11. 8 : 4 = 2

12. (4 ? 8 ) : 4 = 8

IV. Układanie zadań.

• Polecenie dla ucznia: Wybierz dowolne pytanie z tablicy i ułóż do niego treść zadania o podobnej tematyce. Rozwiąż je samodzielnie i zapisz odpowiedź.

Walory metody kruszenia:

• Jest to atrakcyjna dla uczniów metoda pracy, polegająca na wymyślaniu pytań i odpowiedzi w postaci formuły matematycznej ( poprzedzonych ułożeniem w myślach zadania i znalezieniem związku między danymi liczbowymi a niewiadomą zawartą w pytaniu ).

• Rozwija myślenie ideacyjne ( wytwarzające pomysły ) i krytyczno - logiczne ( oceniające pomysły ).

• Uczy dostrzegania związków i zależności w zadaniach tekstowych, wykorzystywanych do tworzenia nowych wersji zadań.

• Uaktywnia uczniów poprzez głośną, zbiorową pracę i pobudza do poszukiwań nowych rozwiązań i dostrzegania różnorodności ( praca samodzielna jednoosobowa jest bardziej uschematyzowana ).

• Ćwiczy płynność myślenia ( chęć układania wielu pytań ), giętkość myślenia ( szybka zmiana kierunku myślenia w związku z dostrzeganiem nowych zależności ), oryginalność myślenia ( układane pytania są coraz bardziej twórcze ).

W geometrii przyjmuje się bez określenia pewną ilość pojęć zwanych pojęciami pierwotnymi. Pozostałe pojęcia określa się, czyli definiuje za pomocą pojęć pierwotnych. Do pierwotnych pojęć w geometrii płaskiej zaliczamy: punkt, prostą, płaszczyznę.

PUNKT





Punkty na płaszczyźnie oznaczamy wielkimi literami alfabetu. Punkty przedstawiamy w postaci kropeczki, kółeczka lub krzyżyka. Nie posiadają one żadnych wymiarów.




Figurą geometryczną nazywamy każdy zbiór punktów.

Ta figura składa się z jednego punktu	Ta figura składa się z trzech punktów	Ta figura składa się z nieskończenie wielu punktów

PROSTA

prosta a	prosta AB   (prosta BA)


Prostą możemy oznaczyć małą literą. Prostą też można oznaczyć dwiema dużymi literami, które oznaczają punkty należącej do tej prostej.




Przez jeden punkt przechodzi nieskończenie wiele prostch	Przez dwa punkty przechodzi dokładnie jedna prosta




Wzajemne położenie prostych

prosta a b Prosta a jest prostopadła do prostej b	prosta a || b Prosta a jest równoległa do prostej b

PÓŁPROSTA





Każdy punkt należący do prostej wyznacza dwie półproste.

półprosta a	półprosta AB


Półprostą możemy oznaczyć małą literą. Półprostą też można oznaczyć dwiema dużymi literami: pierwsza z tych liter oznacza początek półprostej.

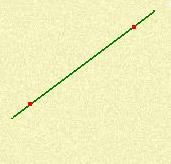
ODCINEK




                                                        odcinek AB


Dwa punkty należące do prostej wyznaczają odcinek. Punkty te nazywamy końcami odcinka.

ŁAMANA




Łamana to figura geometryczna utworzona z odcinków (zwanych jej bokami) w taki sposób, że:

• żadne dwa następujące po sobie odcinki nie leżą na jednej prostej

• koniec pierwszego odcinka jest początkiem drugiego odcinka, koniec drugiego - początkiem trzeciego i tak dalej.

Rodzaje łamanych

łamana zamknięta	łamana otwarta	łamana wiązana

WIELOKĄT




Wielokąt to część płaszczyzny, ograniczona łamaną zamkniętą, wraz z tą łamaną. Boki łamanej nazywamy bokami wielokąta. Wierzchołki łamanej nazywamy wierzchołkami wielokąta.

Nazwy wielokątów pochodzą od ilości kątów wewnętrznych w danym wielokącie np:

trójkąt	czworokąt	pięciokąt





Wielokąt nazywamy wypukłym, jeżeli odcinek łaczący dowolne dwa punkty tego wielokąta zawiera się w tym wielokącie.
Wielokąt, który nie jest wypukły nazywamy wklęsłym.

wielokąt wypukły	wielokąt wklęsły








Odcinek, którego końcami są wierzchołki wielokata i który nie jest jego bokiem, nazywamy przekatną tego wielokąta.

Obwodem wielokąta nazywamy długość łamanej, wyznaczajacej ten wielokąt, a więc sumę długości boków tego wielokąta.

---