5. Kwantyfikatory.

Kwantyfikator to termin przyjęty w matematyce i logice matematycznej na oznaczenie zwrotów: dla każdego oraz istnieje, które odgrywają ważną rolę w formułowaniu twierdzeń i definicji matematycznych

Rachunek predykatów pierwszego rzędu (ang. First order predicate calculus) to system logiczny, w którym kwantyfikatory mogą mówić tylko o obiektach, nie zaś o ich zbiorach. Rachunek ten też często nazywamy rachunkiem kwantyfikatorów. System rachunku predykatów pierwszego rzędu składa się z:

• Stałych,

• Funkcji n-argumentowych dla pewnego n naturalnego,

• Relacji n-argumentowych dla pewnego n naturalnego,

• Relacji logicznych

• Kwantyfikatora ogólnego i kwantyfikatora szczegółowego.

Jeśli funkcja zdaniowa ϕ(x), x∈X jest zdaniem prawdziwym dla każdego elementu zakresu zmienności, to piszemy

lub krócej

co odczytujemy „dla każdego x ϕ(x)”. Jest to kwantyfikator ogólny(uniwersalny, duży). Inne oznaczenie tego kwantyfikatora to ∀ (z ang. All -każdy).

Jeśli funkcja zdaniowa ϕ(x), x∈X jest zdaniem prawdziwym dla co najmniej jednego (czyli dla pewnego) elementu zakresu zmienności, to piszemy

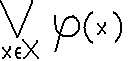
lub krócej

co odczytujemy „dla pewnego x ϕ(x)”. Jest to kwantyfikator szczegółowy(egzystencjalny, mały). Inne oznaczenie tego kwantyfikatora to ∃ (z ang. Exist -istnieje).

Przykład 4.1.Stwierdzenie, że dla każdej liczby rzeczywistej wyrażenie x²+4 przyjmuje wartości dodatnie, przy pomocy kwantyfikatora zapisujemy

Przykład 4.2.Stwierdzenie, że istnieją takie liczby rzeczywiste, które spełniają równanie x²-4=0 , przy pomocy kwantyfikatora zapisujemy

Zmienna występująca pod znakiem kwantyfikatora nazywa się zmienną związaną danym kwantyfikatorem. Natomiast zmienna występująca w wyrażeniu matematycznym, która nie jest związana żadnym kwantyfikatorem, nazywa się zmienną wolną. Wyrażenie następujące po kwantyfikatorze, objęte tym kwantyfikatorem, nazywa się zasięgiem kwantyfikatora. Jeżeli w zasięgu kwantyfikatora znajdują się jakieś inne kwantyfikatory, to kwantyfikator początkowy wiąże tylko te zmienne, które nie są związane żadnym kwantyfikatorem zawartym w jego zasięgu. Stosując kwantyfikator do formy zdaniowej, otrzymuje się nową formę zdaniową lub zdanie. Pozwalają one budować nowe predykaty (nowe funkcje zdaniowe) z już istniejących.

Przykład 4.3.Rozpatrzmy wyrażenie {
}. Zmienna x jest objęta tylko kwantyfikatorem szczegółowym wobec tego jest związana przez ten kwantyfikator zaś jest wolna dla kwantyfikatorem ogólnego. Natomiast zmienna y jest objęta tylko kwantyfikatorem ogólnym wobec tego jest związana przez ten kwantyfikator zaś jest wolna względem kwantyfikatora ogólnego szczegółowego.

Przykład 4.4.Rozpatrzmy wyrażenie {
}. Jest ono równoważne formie zdaniowej z Przykładu 4.3. Zmienna oznaczona symbolem x jest objęta kwantyfikatorem szczegółowym i jest związana przez ten kwantyfikator. Natomiast ponowne oznaczenie zmiennej symbolem x powoduje, że staje się ona związana przez kwantyfikator ogólny. Oczywiście są to zmienne oznaczone jedynie takim samym symbolem.

Przykład 4.5.Rozpatrzmy wyrażenie {
}. Mamy dla
-x zmienna związana oraz
-y związana zaś x wolna.

Przykład 4.6.Rozpatrzmy wyrażenie {
} nie jest ono równoważne wyrażeniu z Przykładu 4.5 .

Prawa rachunku kwantyfikatorów

Niech ϕ(x) i ψ(x) będą funkcjami zdaniowymi o zakresie w zbiorze X:

1. Prawa de'Morgana dla kwantyfikatorów

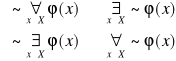
2. Prawa rozdzielności

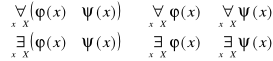
3.

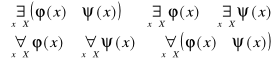
4.

Przykład 4.7 .Niech X=N , ϕ(x) -„x jest liczbą parzystą” i ψ(x) -„x jest liczbą nieparzystą”. Wówczas forma zdaniowa

• 
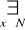
  (x jest liczbą parzystą) ∧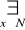
  (x jest liczbą nieparzystą)

jest prawdziwa, ale

(x jest liczbą parzystą ∧ x jest liczbą nieparzystą)

jest fałszywe.

Fakt ten jest dowodzi, że w 3, pierwszej implikacji odwrócić nie można.

• 
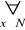
  (x jest liczbą parzystą ∨ x jest liczbą nieparzystą)

jest prawdziwa, ale

(x jest liczbą parzystą) ∨
(x jest liczbą nieparzystą)

jest fałszywe.

Fakt ten jest dowodzi, że w 3, drugiej implikacji odwrócić nie można.

• 
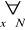
  (x jest liczbą parzystą ) ⇒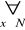
  ( x jest liczbą nieparzystą)

jest prawdziwa(„fałszu zawsze mamy prawdę”), ale

(x jest liczbą parzystą ⇒ x jest liczbą nieparzystą)

jest fałszywe.

Niech ϕ(x,y) oznacza funkcję zdaniową zmiennych: x o zakresie X i y o zakresie Y. Wówczas:

1.

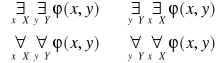
2.

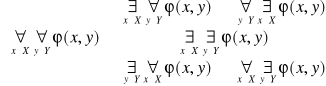
Przykład 4.8.Niech X=Y=R , ϕ(x, y):=(x < y).Wówczas

jest zdaniem prawdziwym

jest zdaniem fałszywym

Kwantyfikatory ograniczone.

Niech ϕ(x) i ψ(x) będą funkcjami zdaniowymi o zakresie X. Wyrażenia

oznacza

oznacza

Przykład 4.9. Niech X=R₊ , ϕ(x):= (x ≥ 1) i ψ(x):=(ln x ≥ 0).Wyrażenie

oznacza

oznacza

Przykład 4.10. Niech X=R, zdanie

• Dla
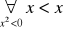
  jest zdaniem prawdziwym oznacza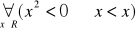
  

• 
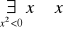
  jest zdanie, fałszywym oznacza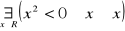
  

ZADANIA

5.1. Zakładając, że dziedziną każdej funkcji zdaniowej jest zbiór liczb rzeczywistych wskazać, które z następujących zdań są prawdziwe, a które fałszywe:

a)
(sin²x+cos²x=1), b)
(sin²x+cos²x=2) (sin x/2=1),

c)
(sin2x=2sinx), d)
(sin2x=2sinx),

e) ~
(
=x), f)
(2^x=-2),

g)
(x²-3x=0), h)
(x+1>0),

i)
(sin x/2=1), j)
(sin x/2=1),

k)
(|x|>0), l)
[(x<-1)⇒(x<0)],

m)
[(x=0)∨ (|x|>0)].

1. Dla funkcji zdaniowych:

1. 
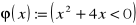
   ; b)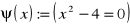
   ;

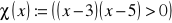
2. 
   ; c)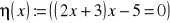
   ,

podać wartość logiczną zdań i zapisać ich negację

1. 
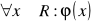
   ; 2)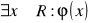
   ;

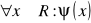
2. 
   ; 3)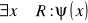
   ;

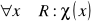
3. 
   ; 4)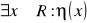
   .

2. Dla funkcji zdaniowych

1. 
   ;

2. 
   ;

3. 
   ;

4. 
   .

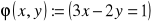
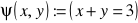
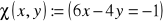
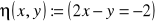
Zapisać zdania i podać ich wartości logiczne

1)
,
;

2)
,
;

3)
,
;

4)
.

2. Zapisać przy pomocy kwantyfikatorów i funktorów następujące sformułowania

1. dla każdej liczby rzeczywistej x,
   ;

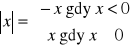
2. wartość bezwzględna sumy dwóch liczb rzeczywistych jest niewiększa od sumy wartości bezwzględnych tych liczb;

3. nie dla każdej liczby rzeczywistej jej kwadrat jest większy od tej liczby

4. dla dowolnego m równanie mx²-mx-2m=0 ma rozwiązanie.

5. x jest liczbą parzystą

6. nie istnieje największa liczba naturalna

7. nie istnieje liczba, której kwadrat byłby mniejszy od zera

8. f(x) jest funkcją malejącą

9. ciąg {a_n} jest rosnący

---