sprawozdanie 12 got zal, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka lab skrypty, Fizyka, Sprawozdanie 12

Politechnika Śląska Katowice, dnia 13.04.11r.

Wydział Transportu

ĆWICZENIA LABOLATORYJNE Z FIZYKI

Sprawozdanie z ćwiczenia nr 12

Temat ćwiczenia: Wyznaczanie pracy wyjścia elektronów z metali w badaniach emisji termoelektronowej.

Grupa T15

Sekcja nr 7

Cabon Tomasz

Majran Kamil

Pyszny Marcin

OBLICZENIA

I. Obliczanie oporu Katody R_t odpowiednio dla U_ż = 3,54 V, I_ż= 2,2A i U_ż = 4,14V, I_ż= 2,4A

U_ż₁= 3,54 [V] Δ U_ż1= 0,5%* U_ż1

I_ż₁= 2,2 [A] Δ I_ż₁= 0,5%* I_ż1

Obliczenie niepewności wszystkich uzyskanych wyników wynikające z klasy dokładności użytych przyrządów pomiarowych.

Obliczenie niepewności pomiarowych.

napięcie anodowe U_a [V]	niepewność U_a [V]	Natężenie prądu anodowego I_ax10^-6[A]	Niepewność I_a x10^-6 [A]
0	0	0	0
10	0,005	0	0
20	0,01	1	0,0005
30	0,015	7	0,0035
40	0,02	24	0,012
50	0,025	43	0,0215
60	0,03	59	0,0295
70	0,035	76	0,038
80	0,04	97	0,0485
90	0,045	116	0,058
100	0,05	138	0,069
110	0,055	153	0,0765
120	0,06	156	0,078
130	0,065	159	0,0795
140	0,07	160	0,08
150	0,075	162	0,081
160	0,08	164	0,082
170	0,085	166	0,083
180	0,09	167	0,0835
190	0,095	169	0,0845
200	0,1	170	0,085
210	0,105	171	0,0855
220	0,11	173	0,0865
230	0,115	174	0,087
240	0,12	175	0,0875
250	0,125	177	0,0885
Średnia	0,0625		0,058788

Obliczenie oporu katody R_t₁_.

R_t1= U_ż₁/I_ż₁

Obliczenie niepewności wyznaczenia R_tmetodą różniczki zupełnej.

gdzie:

ΔU₁ = 0,0625 [V]

ΔI₁ = 0,058788 [A]

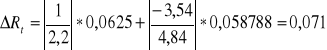
0x01 graphic

U_ż₂= 4,14 [V] Δ U_ż₂= 0,5%* U_ż₂

I_ż₂= 2,4 [A] Δ I_ż₂= 0,5%* I_ż₂

Obliczenie niepewności pomiarowych.

napięcie anodowe U_a [V]	niepewność U_a [V]	Natężenie prądu anodowego I_a x10^-6[A]	Niepewność I_a x10^-6 [A]
0	0	0	0
10	0,005	0	0
20	0,01	4	0,002
30	0,015	19	0,0095
40	0,02	49	0,0245
50	0,025	90	0,045
60	0,03	142	0,071
70	0,035	201	0,1005
80	0,04	267	0,1335
90	0,045	339	0,1695
100	0,05	408	0,204
110	0,055	481	0,2405
120	0,06	556	0,278
130	0,065	615	0,3075
140	0,07	662	0,331
150	0,075	687	0,3435
160	0,08	695	0,3475
170	0,085	702	0,351
180	0,09	710	0,355
190	0,095	716	0,358
200	0,1	723	0,3615
210	0,105	729	0,3645
220	0,11	735	0,3675
230	0,115	741	0,3705
240	0,12	747	0,3735
250	0,125	751	0,3755
Średnia	0,0625		0,226327

Obliczenie oporu katody R_t

R_t₂= U_ż₂/I_ż₂

Obliczenie niepewności wyznaczenia R_tmetodą różniczki zupełnej.

gdzie:

ΔU₂ = 0,0625 [V]

ΔI₂ = 0,226327 [A]

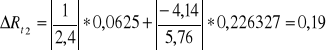
0x01 graphic

U_ż3= 4,7 [V] Δ U_ż3= 0,5%* U_ż₃

I_ż3= 2,6 [A] Δ I_ż3= 0,5%* I_ż₃

Obliczenie niepewności pomiarowych.

napięcie anodowe U_a [V]	niepewność U_a [V]	Natężenie prądu anodowego I_ax10^-6[A]	Niepewność I_a x10^-6 [A]
0	0	0	0
10	0,005	1	0,0005
20	0,01	11	0,0055
30	0,015	36	0,018
40	0,02	79	0,0395
50	0,025	134	0,067
60	0,03	205	0,1025
70	0,035	292	0,146
80	0,04	394	0,197
90	0,045	509	0,2545
100	0,05	641	0,3205
110	0,055	796	0,398
120	0,06	957	0,4785
130	0,065	1139	0,5695
140	0,07	1323	0,6615
150	0,075	1502	0,751
160	0,08	1665	0,8325
170	0,085	1805	0,9025
180	0,09	1921	0,9605
190	0,095	2000	1
200	0,1	2060	1,03
210	0,105	2110	1,055
220	0,11	2150	1,075
230	0,115	2170	1,085
240	0,12	2190	1,095
250	0,125	2210	1,105
Średnia	0,0625		0,544231

Obliczenie oporu katody R_t3.

R_t3= U_ż3/I_ż3

Obliczenie niepewności wyznaczenia R_tmetodą różniczki zupełnej.

gdzie:

ΔU = 0,0625 [V]

ΔI = 0,544231 [A]

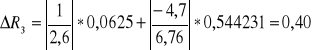
0x01 graphic

Zależność rezystancji katody od jej temperatury

R [Ω]	1,39	1,5	1,59	1,66	1,77
T [K]	2000	2100	2250	2350	2450

Wykres R_t = f(T) unormowanej rezystancji jako funkcji jej temperatury wraz z prostą aproksymującą R_t = f(T) w zakresie temperatur 1273-2273°C=1546-2546 K

Aproksymacja wykresu metodą najmniejszych kwadratów oraz niepewności a i b metodą różniczki zupełnej.

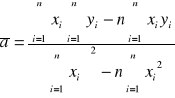
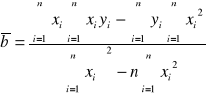
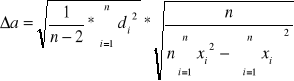
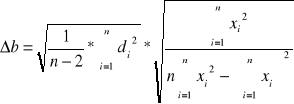
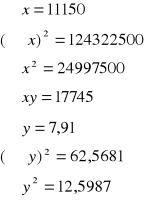
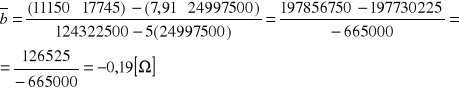
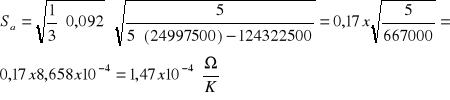
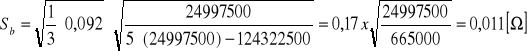
0x01 graphic

= (
0 ± 0,00015) [Ω/K]

= (-0,190 ± 0,011) [Ω]

Wykorzystując wartości współczynników kierunkowych prostej aproksymującej
obliczyć temperatury katody T odpowiadające rezystancjom katody wyznaczonym w p.A6. korzystamy ze wzoru:

gdzie:

Metodą różniczki zupełnej obliczyć niepewność wyznaczania wielkości T

= 421,97+13,75+88,75 = 524,47 [K]

=450+13,75+237,5 = 701,25 [K]

=468,75+13,75+500 = 982,5 [K]

Odczytanie z wykresów wartości prądów nasycenia I_an1i I_an2odpowiadające temperaturom T₁, T₂

I_an1=16×10^-⁶ [A]

I_an2=695×10^-⁶ [A]

I_an3=2000×10^{- 6} [A]

Wyznaczenie pracy W wyjścia elektronów z metalu katody

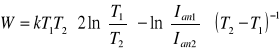
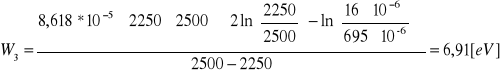
0x01 graphic

Wartość średnia pracy wyjścia elektronów z metalu katody.

Odchylenie standardowe

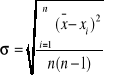
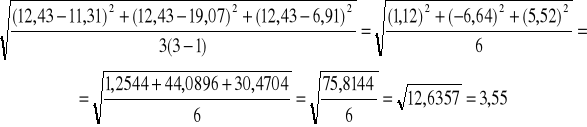
0x01 graphic

=3,55

W_śr=[12,43±3,55) [eV]

Zestawienie wyników:

= (
0 ± 0,00015) [Ω/K]

= (-0,190 ± 0,011) [Ω]

y= 0,0008x - 0,190 - prosta aproksymująca

I_an1=16×10^{- 6} [A]

I_an2=695×10^{- 6} [A]

I_an3=2000×10^{- 6} [A]

W_śr=[12,43±3,55) [eV]

Wnioski:

Celem ćwiczenia było wyznaczenie pracy wyjścia elektronów z metali w badaniach emisji termoelektrycznej.

Wyniki naszych obliczeń obarczone są błędami pomiarowymi wynikającymi z klasy dokładności użytych przyrządów pomiarowych jak i również z niedokładności odczytów wielkości pomiarowych.

Do obliczenia pracy wyjścia elektronów z metalu wykorzystany został wzór Richardsona, który określa natężenie prądu płynącego przez diodę ( prąd nasycenia). Obliczając wartość średnią i odchylenie standardowego otrzymanych wyników pracy wyjścia elektronów z metalu uzyskaliśmy wartość W_śr=[12,43±3,55) [eV]