MATERIAŁY POMOCNICZE DO LABORATORIÓW

Z BADAŃ OPERACYJNYCH

Badania operacyjne: wybrane zagadnienia programowania liniowego - rozwiązywanie zadań z wykorzystaniem modułu Solver.

1. WYBÓR STRUKTURY ASORTYMENTOWEJ PRODUKCJI

Zad.1 str. 23. Badania operacyjne w przykładach i zadaniach pod red. K. Kukuły, PWN: Warszawa 2001.

Zakład produkuje dwa wyroby, które są wykonywane na dwóch obrabiarkach: O₁ oraz O₂ i na frezarce F. Czas pracy tych maszyn jest ograniczony i wynosi, odpowiednio, dla obrabiarki O₁ - 33 000 godz., dla obrabiarki O₂ - 13 000 godz. i dla frezarki - 80 000 godz. Zużycie czasu pracy maszyn (w godz.) na produkcję jednostki każdego z wyrobów podano w poniższej tabeli.

Maszyny	Zużycie czasu pracy na jednostkę wyrobu
		I	II
O1	3	1
O2	1	1
F	5	8

Zysk ze sprzedaży wyrobu I wynosi 1 zł, ze sprzedaży wyrobu II - 3 zł. Z analizy sprzedaży z lat ubiegłych wynika, że wyrobu II nie będzie można sprzedać więcej iż 7 000 szt.

Zaplanować strukturę asortymentową produkcji tak, aby przy przyjętych ograniczeniach zysk ze sprzedaży wyrobów był jak największy.

Rozwiąż zadanie programowania liniowego stosując moduł Solver /Excel/.

Postać standardowa modelu:

Fc: X1 + 3X2 → MAX

Wo. 3X1 + X2 ≤ 33 000 (1.)

X1 + X2 ≤ 13 000 (2.)

5X1 + 8X2 ≤ 80 000 (3.)

X2 ≤ 7 000 (4.)

Xi ≥ 0

Algorytm rozwiązania - moduł Solver /Excel/

1. Korzystamy z modelu decyzyjnego w postaci standardowej.

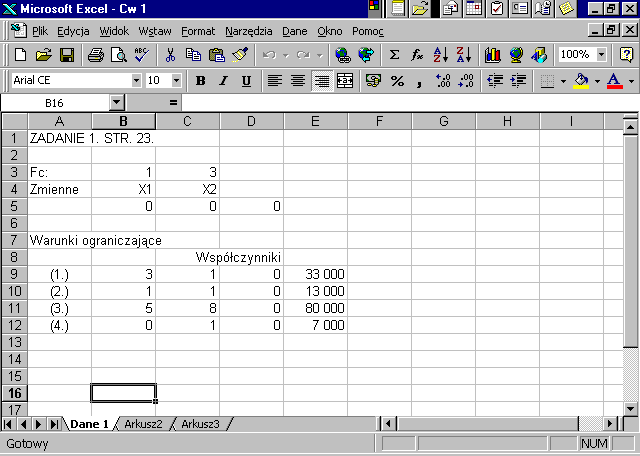
2. Otwieramy arkusz Excel-a, nazywamy go zad.1.Wprowadzamy dane w następujący sposób:

a/ współczynniki funkcji celu (wagi funkcji celu) w zakres: B3:C3,

b/ zmienne decyzyjne w zakres: B4:C4,

c/ wartości początkowe zmiennych decyzyjnych (dla każdej zmiennej wpisujemy wartość początkową 0) w zakres: B5:C5,

d/ współczynniki warunków ograniczających w zakres: B9:C12,

e/ wyrazy wolne warunków ograniczających w zakres: E9:E12,

f/ komórkę D5 przeznaczamy na wartość funkcji celu dla bieżących wartości zmiennych decyzyjnych; w komórce tej wprowadzamy funkcję Excel-a: SUMA.ILOCZYNÓW(B3:C3;B5:C5),

g/ w komórkach D9:D12 zapisujemy formuły obliczania wartości lewych stron warunków ograniczających zadania optymalizacyjnego dla bieżących wartości zmiennych decyzyjnych według wzoru D9:=SUMA.ILOCZYNÓW(B9:C9;$B$5:$C$5); (F4 - skrót klawiszowy wprowadzający adres bezwzględny). Formułę z komórki D9 kopiujemy do komórek D10, D11, D12.

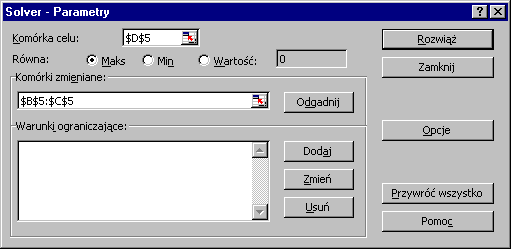
3. Wybieramy z menu Narzędzia opcję Solver. Wyświetli się okno dialogowe Solver - Parametry.

4. W okno Komórka celu wprowadzamy adres komórki z formułą obliczania wartości funkcji celu ($D$5).

5. Wybieramy jedno z kryteriów optymalizacji. W naszym zadaniu będzie to Maks.

6. 
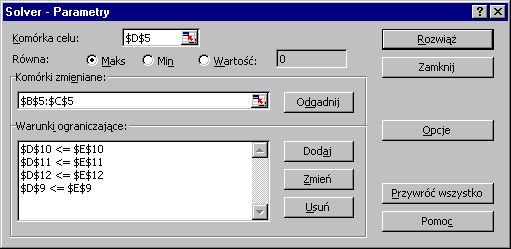
   W polu Komórki zmieniane wprowadzamy zakres komórek, w które wcześniej wpisaliśmy wartości zerowe zmiennych decyzyjnych ($B$5:$C$5).

7. W pole Warunki ograniczające za pomocą przycisku Dodaj wprowadzamy kolejne warunki ograniczające.

8. Otworzy się okno Dodaj warunek ograniczający. W polu Adres komórki wprowadzamy adres komórki zawierającej formułę obliczania wartości lewej strony pierwszego warunku ograniczającego ($D$9), następnie wybieramy symbol właściwej relacji (<=), a w polu Warunek ograniczający wprowadzamy adres komórki zawierającej wartość wyrazu wolnego pierwszego warunku ograniczającego ($E$9). W analogiczny sposób dodajemy kolejne warunki ograniczające.

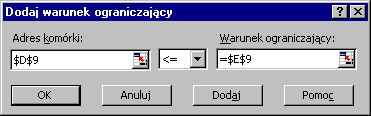
9. Po wprowadzeniu ostatniego warunku ograniczającego klikamy OK i wracamy do okna Solver - Parametry.

10. 
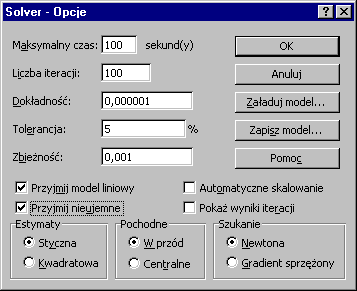
    Klikamy w oknie dialogowym w Opcje i zaznaczamy: Przyjmij model liniowy oraz Przyjmij nieujemne (warunek nieujemności zmiennych decyzyjnych - X_j ≥ 0). Potwierdzamy polecenie OK.

9. 
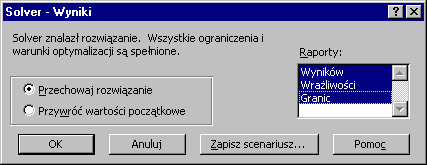
   W oknie Solver - Parametry klikamy przycisk Rozwiąż i otrzymujemy okno dialogowe, w którym zaznaczamy raporty: Wyników, Wrażliwości i Granic.

10. 
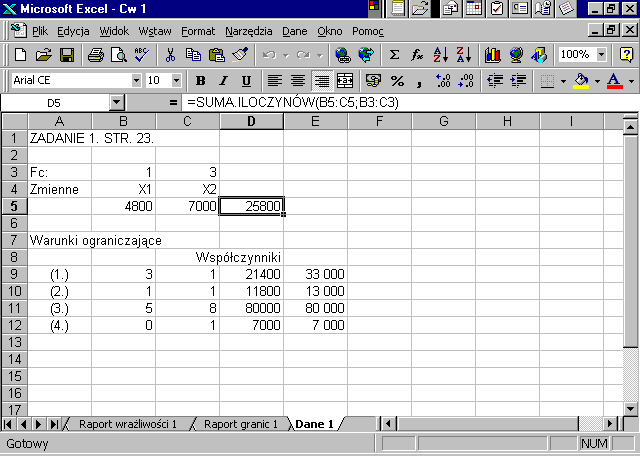
    Rozwiązanie zadania otrzymujemy zarówno w arkuszu, w którym wprowadzaliśmy dane jak i w Raporcie wyników.

11. Sprawdźmy jeszcze, wykorzystując raporty wyników i wrażliwości w Solverze, czy otrzymane rozwiązanie jest jedynym rozwiązaniem optymalnym:

a/ jeżeli w raporcie wrażliwości wartość końcowa i przyrost krańcowy zmiennej decyzyjnej są równe zero to występuje nieskończenie wiele rozwiązań optymalnych,

b/ jeżeli zależności te dla zmiennych decyzyjnych nie są spełnione, to dla każdego warunku ograniczającego sprawdzamy wartość ceny dualnej:

• jeżeli przynajmniej w jednym przypadku cena dualna jest równa zero i

• odpowiedni warunek ograniczający jest wiążący (w raporcie wyników) to zadanie ma nieskończenie wiele rozwiązań optymalnych.

Microsoft Excel 8.0a Raport wyników
Komórka celu (Maks)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$D$5		0	25800
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$5	X1	0	4800
	$C$5	X2	0	7000
Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$D$9	(1.) Współczynniki	21400	$D$9<=$E$9	Nie wiążące	11600
	$D$10	(2.) Współczynniki	11800	$D$10<=$E$10	Nie wiążące	1200
	$D$11	(3.) Współczynniki	80000	$D$11<=$E$11	Wiążące	0
	$D$12	(4.) Współczynniki	7000	$D$12<=$E$12	Wiążące	0

Microsoft Excel 8.0a Raport wrażliwości
Komórki decyzyjne
			Wartość	Przyrost	Współczynnik	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	krańcowy	funkcji celu	wzrost	spadek
	$B$5	X1	4800	0	1	0,875	1
	$C$5	X2	7000	0	3	1E+30	1,4
Warunki ograniczające
			Wartość	Cena	Prawa strona	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	dualna	w. o.	wzrost	spadek
	$D$9	(1.) Współczynniki	21400	0	33000	1E+30	11600
	$D$10	(2.) Współczynniki	11800	0	13000	1E+30	1200
	$D$11	(3.) Współczynniki	80000	0,2	80000	6000	24000
	$D$12	(4.) Współczynniki	7000	1,4	7000	3000	2000

Microsoft Excel 8.0a Raport granic
		Cel	Wartość
	Komórka	Nazwa	końcowa
	$D$5		25800
		Zmienne decyzyjne	Wartość		Dolna	Cel		Górna	Cel
	Komórka	Nazwa	końcowa		granica	Wynik		granica	Wynik
	$B$5	X1	4800		0	21000		4800	25800
	$C$5	X2	7000		0	4800		6999,999859	25799,99958

W związku z tym, że dla rozwiązywanego zadania nie są spełnione wymienione warunki istnieje tylko jedno rozwiązanie optymalne.

Rozwiązanie:

X1 = 4800 szt.

X2 = 7000 szt.

Fc. = 25 800 zł

2. PROBLEM MIESZANKI

Rozwiąż zadanie stosując moduł Solver.

Zadanie 2.

Racjonalna hodowla Pokėmonów wymaga dostarczenia dziennie każdemu osobnikowi trzech składników odżywczych A, B i C w następujących ilościach: składnika A co najmniej 4 jednostki wagowe; składnika B dokładnie 4 jednostki, a składnika C co najwyżej 6 jednostek wagowych. Składniki te zawarte są w trzech rodzajach galaretek tazos: czarnej, niebieskiej oraz fioletowej. W poniższej tablicy podano zawartość każdego ze składników w 1kg galaretki oraz ceny zakupów tych galaretek.

Zawartość składnika w 1 kg galaretki	Galaretki			Dzienna norma zapotrzebowania
		Czarna	Niebieska		Fioletowa
A	1	1	3	4
B	2	1	1	4
C	0	2	3	6
CENA	2	2	1

Jakie ilości poszczególnych galaretek należy zakupić, aby dzienne koszty wyżywienia Pokėmonów były możliwie najniższe?

Algorytm rozwiązania - moduł Solver /Excel/.

Postać standardowa modelu:

Fc: 2X1 + 2X2 + X3 → MIN

Wo. X1 + X2 + 3X3 ≥ 4 (1.)

2X1 + X2 + X3 = 4 (2.)

2X2 + 3X3 ≤ 6 (3.)

Xi ≥ 0

1. Korzystamy z modelu decyzyjnego w postaci standardowej.

2. Otwieramy nowy arkusz Excel-a, nazywamy go zad.2. Wprowadzamy dane w następujący sposób:

a/ współczynniki funkcji celu (wagi funkcji celu) w zakres: C2:E2,

b/ zmienne decyzyjne w zakres: C3:E3,

c/ wartości początkowe zmiennych decyzyjnych (dla każdej zmiennej wpisujemy wartość początkową 0) w zakres: C4:E4,

d/ współczynniki warunków ograniczających w zakres: C7:E9,

e/ wyrazy wolne warunków ograniczających w zakres: G7:G9,

f/ komórkę F4 przeznaczamy na wartość funkcji celu dla bieżących wartości zmiennych decyzyjnych; w komórce tej wprowadzamy funkcję Excel-a: =SUMA.ILOCZYNÓW(C2:E2;C4:E4),

g/ w komórkach F7:F9 zapisujemy formuły obliczania wartości lewych stron warunków ograniczających zadania optymalizacyjnego dla bieżących wartości zmiennych decyzyjnych według wzoru F7: =SUMA.ILOCZYNÓW(C7:E7;$C$4:$E$4); formułę z komórki F7 kopiujemy do komórek F8, F9.

3. Wybieramy z menu Narzędzia opcję Solver. Wyświetli się okno dialogowe Solver - Parametry.

4. W okno Komórka celu wprowadzamy adres komórki z formułą obliczania wartości funkcji celu ($F$4).

5. Wybieramy jedno z kryteriów optymalizacji. W naszym zadaniu będzie to Min.

6. W polu Komórki zmieniane wprowadzamy zakres komórek, w które wcześniej wpisaliśmy wartości zerowe zmiennych decyzyjnych ($C$4:$E$4).

7. W pole Warunki ograniczające za pomocą przycisku Dodaj wprowadzamy kolejne warunki ograniczające.

8. Otworzy się okno Dodaj warunek ograniczający. W polu Adres komórki wprowadzamy adres komórki zawierającej formułę obliczania wartości lewej strony pierwszego warunku ograniczającego ($F$7), następnie wybieramy symbol właściwej relacji (>=), a w polu Warunek ograniczający wprowadzamy adres komórki zawierającej wartość wyrazu wolnego pierwszego warunku ograniczającego ($G$7). W analogiczny sposób dodajemy kolejne warunki ograniczające.

9. 
   Po wprowadzeniu ostatniego warunku ograniczającego klikamy OK i wracamy do okna Solver - Parametry.

10. Klikamy w oknie dialogowym w Opcje i zaznaczamy: Przyjmij model liniowy oraz Przyjmij nieujemne (warunek nieujemności zmiennych decyzyjnych - X_j ≥ 0), potwierdzamy OK.

11. W oknie Solver - Parametry klikamy przycisk Rozwiąż i otrzymujemy okno dialogowe, w którym zaznaczamy raporty: Wyników, Wrażliwości i Granic.

12. Rozwiązanie zadania otrzymujemy zarówno w arkuszu, w którym wprowadzaliśmy dane jak i w Raporcie wyników.

13. Sprawdzamy, czy uzyskane rozwiązanie optymalne jest jedynym rozwiązaniem, czy też jest jednym z nieskończenie wielu rozwiązań optymalnych.

A/ Jeżeli w raporcie wrażliwości wartość końcowa i przyrost krańcowy zmiennej decyzyjnej są równe zero to występuje nieskończenie wiele rozwiązań optymalnych.

B/ Jeżeli zależności te dla zmiennych decyzyjnych nie są spełnione, to dla każdego warunku ograniczającego sprawdzamy wartość ceny dualnej:

1. jeżeli przynajmniej w jednym przypadku cena dualna jest równa zero i

2. odpowiedni warunek ograniczający jest wiążący (w raporcie wyników) to zadanie ma nieskończenie wiele rozwiązań optymalnych,

W związku z tym, że dla pierwszego warunku ograniczającego cena dualna jest równa zero, a warunek jest wiążący istnieje nieskończenie wiele rozwiązań optymalnych.

Microsoft Excel 8.0a Raport wrażliwości
Komórki decyzyjne
			Wartość	Przyrost	Współczynnik	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	krańcowy	funkcji celu	wzrost	spadek
	$B$4	x1	1,6	0	2	0	1E+30
	$C$4	x2	0	1	2	1E+30	1
	$D$4	x3	0,8	0	1	5	0
Warunki ograniczające
			Wartość	Cena	Prawa strona	Dopuszczalny	Dopuszczalny
	Komórka	Nazwa	końcowa	dualna	w. o.	wzrost	spadek
	$E$6		4	0	4	3	2
	$E$7		4	1	4	4	2,666666667
	$E$8		2,4	0	6	1E+30	3,6

Microsoft Excel 8.0a Raport wyników
Komórka celu (Min)
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$E$4		0	4
Komórki decyzyjne
	Komórka	Nazwa	Wartość początkowa	Wartość końcowa
	$B$4	x1	0	1,6
	$C$4	x2	0	0
	$D$4	x3	0	0,8
Warunki ograniczające
	Komórka	Nazwa	Wartość komórki	formuła	Status	Luz
	$E$6		4	$E$6>=$F$6	Wiążące	0
	$E$7		4	$E$7=$F$7	Wiążące	0
	$E$8		2,4	$E$8<=$F$8	Nie wiążące	3,6

Microsoft Excel 8.0a Raport granic
		Cel	Wartość
	Komórka	Nazwa	końcowa
	$F$4		4
		Zmienne decyzyjne	Wartość		Dolna	Cel		Górna	Cel
	Komórka	Nazwa	Końcowa		granica	Wynik		granica	Wynik
	$C$4	x1	1,6		1,6	4		1,6	4
	$D$4	x2	0		0	4		0	4
	$E$4	x3	0,8		0,8	4		0,8	4

10

Wyrazy wolne warunków ograniczających

Wartości lewych stron warunków ograniczających

Wartość funkcji celu

Współczynniki warunków ograniczających

Wartości początkowe zmiennych decyzyjnych

Zmienne decyzyjne

Wagi funkcji celu

---