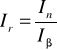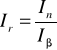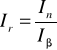Realne stopy procentowe
depozytów złotowych i dewizowych
w banku BGŻ w lutym 2003 r.
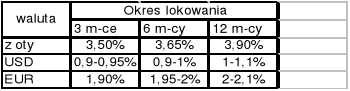
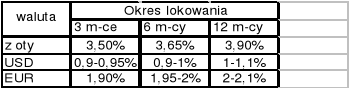
Bank BGŻ s.a. na dzień 01.02.2003 r. oferował następujące roczne nominalne oprocentowanie dla lokat złotowych oraz dewizowych:
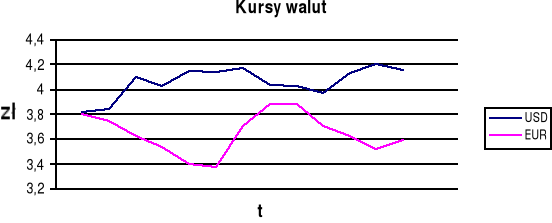
Dla ułatwienia przyjmuje się kursy EUR w taki sposób, że rok 2003 traktuje się jako rok 2001 a jako kursy USD przyjmuje się dane wstecz i w ten sposób kursy USD i EUR będą kształtować się następująco na następne lata:

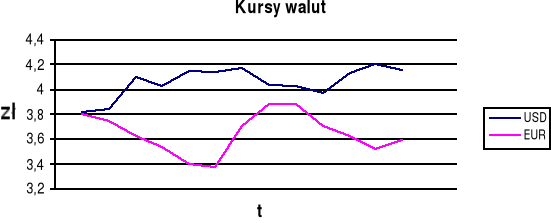

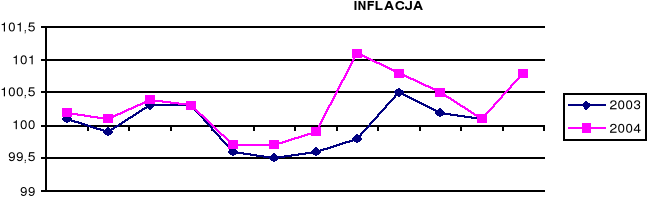
Do obliczenia realnych stóp depozytów niezbędne również będą dane na temat inflacji. Ze względu na niemożliwość posiadania tych informacji, inflację będziemy liczyć wstecz i tak:
3 miesiące
Dane: |
|
|
|
|
zł = |
3,50% |
|
ℓ$1 = |
3,82 zł/$ |
$1= |
0,90% |
|
ℓ$2 = |
4,03 zł/$ |
$2 = |
0,95% |
|
ℓ€1= |
3,80 zł/€ |
€ = |
1,90% |
|
ℓ€2= |
3,54 zł/€ |
gdzie:
αzł - roczna stopa procentowa depozytów złotowych
α$ - roczna stopa procentowa depozytów w dolarach
α€ - roczna stopa procentowa depozytów w euro
ℓ$1 - kurs dolara w stosunku do złotego na początku okresu
ℓ$2 - kurs dolara w stosunku do złotego na koniec okresu
ℓ€1 - kurs euro w stosunku do złotego na początku okresu
ℓ€2 - kurs euro w stosunku do złotego na koniec okresu
β - inflacja za dany okres
|
![]()
I1, I2, ... - indeksy inflacji dla kolejnych miesięcy
In - indeks inflacji w miesiącu, w którym kończy się termin lokaty
![]()
Indeks przyrostu wkładu złotowego
Aby obliczyć indeksy przyrostu wkładów złotowych i dewizowych, należy roczne stopy procentowe tych depozytów zamienić na kwartalne a następnie zamienić je na indeksy i tak otrzymujemy:
|
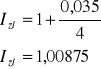
Indeks przyrostu wkładów dewizowych
wkładu dolarowego
![]()
oraz ![]()
wkładu w euro
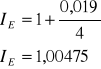
Indeks kursu walutowego
Indeks kursu walutowego obliczamy jako iloraz kursu na koniec okresu i kursu na początek okresu
|
![]()
Indeks bazowy
Indeks ten obliczamy jako iloczyn indeksów łańcuchowych
|
![]()
In$1 = 1,00225 . 1,055 = 1,0574
In$2 = 1,002375 .1,055 = 1,0575
In€ = 1,00475 . 0,9316 = 0,936
Już tutaj widzimy, że nie opłaca się nam zakładać lokaty w euro na okres 3 miesięcy przy takiej zmianie kursów walutowych, nawet jeśli nie bierzemy pod uwagę inflacji. Spadek euro w stosunku do złotego powoduje, że przy takiego rodzaju lokacie tracimy.
Przejście do stóp realnych wg formuły Fishera
|
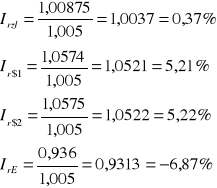
Z powyższych obliczeń wynika, że najbardziej opłacalna okazała się 3 miesięczna lokata dolarowa, której realne oprocentowanie w skali kwartalnej wynosiłoby od 5,21% do 5,22%. Oznacza to, że lokując na niej 1000 zł, po 3 miesiącach wyjęlibyśmy 1052,1 zł, czyli nasz zysk wyniósłby 52,1 zł. Wynika to ze wzrostu wartości dolara w stosunku do złotego oraz stosunkowo niskiej inflacji, choć inflacja jest wyższa od stopy procentowej.
Jeślibyśmy chcieli ulokować te same pieniądze na lokacie o takim samym terminie, lecz złotową, również byśmy zyskali, jednak znacznie mniej, bo jedynie 3,7 zł. Wynika to z faktu, iż oprocentowanie lokaty było wyższe od inflacji w danym okresie.
Najgorszą opcją jest tutaj lokata w euro. W skutek spadku ceny waluty euro oraz z powodu niskiego oprocentowania, które jest niższe od inflacji dla 3 miesięcy, wkład ten przyniósłby nam stratę w wysokości 6,87 grosza na 1 zainwestowaną złotówkę.
6 miesiący
Dane:
zł = |
3,65% |
|
ℓ$1 = |
3,82 zł/$ |
$1= |
0,90% |
|
ℓ$2 = |
4,17 zł/$ |
$2 = |
1,00% |
|
ℓ€1= |
3,80 zł/€ |
€1 = |
1,95% |
|
ℓ€2= |
3,71 zł/€ |
€2 = |
2,00% |
|
|
|
|
![]()
I1, I2, ... - indeksy inflacji dla kolejnych miesięcy
In - indeks inflacji w miesiącu, w którym kończy się termin lokaty
![]()
Jak widać mamy tu do czynienia z deflacją.
Indeks przyrostu wkładu złotowego
|
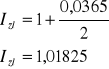
Indeks przyrostu wkładów dewizowych
wkładu dolarowego
![]()
oraz ![]()
wkładu w euro
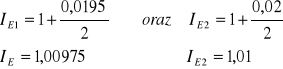
Indeks kursu walutowego
Indeks kursu walutowego obliczamy jako iloraz kursu na koniec okresu i kursu na początek okresu
|
![]()
Indeks bazowy
Indeks ten obliczamy jako iloczyn indeksów łańcuchowych
|
![]()
In$1 = 1,0045 . 1,0916 = 1,0965
In$2 = 1,005 . 1,0916 = 1,0971
In€1 = 1,00975 . 0,9763 = 0,9858
In€2 = 1,01 . 0,9763 = 0,9861
Widzimy tutaj, że nie opłaca się nam zakładać lokaty w euro na okres pół roku przy takiej zmianie kursów walutowych (nie biorąc pod uwagę inflacji). Spadek euro w stosunku do złotego powoduje, że przy takiego rodzaju lokacie tracimy.
Przejście do stóp realnych wg formuły Fishera
|

Jak widzimy na powyższych obliczeniach, najbardziej opłacalna okazała się 6-miesięczna lokata dolarowa (podobnie jak w przypadku lokaty 3-misięcznej), której realne oprocentowanie w skali półrocznej wynosiłoby aż od 10,55% do 10,61%. Oznacza to, że lokując 1000 zł, po 6 miesiącach wyjęlibyśmy 1105,5 zł, czyli nasz zysk wyniósłby 105,5zł. Wynika to z dużego wzrostu wartości dolara w stosunku do złotego oraz występującej w tym okresie deflacji. Możemy tu zauważyć jak ogromny wpływ na lokatę dewizową ma kurs waluty.
Jeśli chcielibyśmy ulokować te same pieniądze i na ten sam termin wykupu na lokacie złotowej, również byśmy zyskali, jednak znacznie mniej, bo jedynie 2,66 zł. Jest to wyższe oprocentowanie niż oferowane w banku na 6 miesięcy (3,65%:2=1,825%). Wynika to z zaistniałej w tym okresie deflacji.
Najgorszą opcją do wyboru, podobnie jak dla lokaty 3 miesięcznej, jest lokata w euro. W skutek spadku ceny waluty euro, wkład ten przyniósłby nam stratę w średniej wysokości 6 złotych na 1000 zł zainwestowanych. Trzeba podkreślić, że odnotowalibyśmy stratę pomimo występującej deflacji, która podnosi realne oprocentowanie.
12 miesiący
Dane:
zł = |
3,90% |
|
ℓ$1 = |
3,82 zł/$ |
$1= |
1,00% |
|
ℓ$2 = |
4,16 zł/$ |
$2 = |
1,10% |
|
ℓ€1= |
3,80 zł/€ |
€1 = |
2,00% |
|
ℓ€2= |
3,59 zł/€ |
€2 = |
2,10% |
|
|
|
β - inflacja za dany okres
|
![]()
I1, I2, ... - indeksy inflacji dla kolejnych miesięcy
In - indeks inflacji w miesiącu, w którym kończy się termin lokaty
![]()
Indeks przyrostu wkładu złotowego
Aby obliczyć indeksy przyrostu wkładów złotowych i dewizowych, należy roczne stopy procentowe tych depozytów zamienić na kwartalne a następnie zamienić je na indeksy i tak otrzymujemy:
|
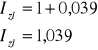
Indeks przyrostu wkładów dewizowych
wkładu dolarowego
![]()
oraz ![]()
wkładu w euro
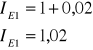
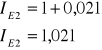
Indeks kursu walutowego
Indeks kursu walutowego obliczamy jako iloraz kursu na koniec okresu i kursu na początek okresu
|
![]()
Indeks bazowy
Indeks ten obliczamy jako iloczyn indeksów łańcuchowych
|
![]()
In$1 = 1,01 . 1,089 = 1,09989
In$2 = 1,011 . 1,089 = 1,1
In€1 = 1,02 . 0,9447 = 0,9636
In€2 = 1,021 . 0,9447 = 0,9645
Już tutaj widzimy, że nie opłaca się nam zakładać lokaty w euro na okres 1 roku przy takiej zmianie kursów walutowych, nawet jeśli nie bierzemy pod uwagę inflacji. Spadek euro w stosunku do złotego powoduje, że przy takiego rodzaju lokacie tracimy.
Przejście do stóp realnych wg formuły Fishera
|
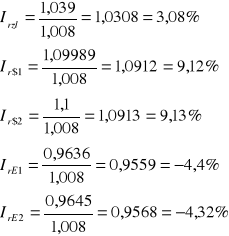
Z powyższych obliczeń wynika, że najbardziej opłacalna okazała się po raz kolejny lokata roczna w dolarach, której realne oprocentowanie wynosiłoby od 9,12% do 9,13%. Oznacza to, że lokując na niej 1000 zł, po roku wyjęlibyśmy 1091,2 zł, czyli nasz zysk wyniósłby 91,2 zł. Wynika to ze wzrostu kursu dolara w stosunku do złotego oraz stosunkowo niskiej inflacji.
Jeślibyśmy chcieli ulokować te same pieniądze na lokacie o takim samym terminie, lecz złotową, również byśmy zyskali, jednak znacznie mniej, bo zaledwie 3,08 zł. Wynika to z faktu, iż oprocentowanie lokaty było wyższe od inflacji w danym okresie.
Najgorszą opcją jest tutaj lokata w euro. W skutek znacznego spadku ceny waluty euro, wkład ten przyniósłby nam stratę w wysokości około 4,36 grosza na 1 zainwestowaną złotówkę. Dodatkową przyczyną straty była inflacja, jednak odbiła się ona na tym wyniku w bardzo niewielkim stopniu.
WNIOSKI KOŃCOWE
Jak można zauważyć, bardzo ryzykowne jest lokowanie pieniędzy we wkłady dewizowe, ponieważ są one silnie związane z kursem walutowym. Choć małe obniżenie kursu waluty, powoduje duże zmiany w realnym oprocentowaniu lokaty. Jak wynika z powyższej analizy, inwestowanie w lokaty dolarowe przyniosłoby ogromne zyski przy terminie 3, 6 i 12 miesięcy. Odwrotny skutek odnieślibyśmy w przypadku lokat w walucie euro. Tu spadek kursu spowodował stratę na lokacie, nawet w sytuacji deflacji. Daje to wyraźny obraz, jak bardzo ryzykowne są lokaty dewizowe. Jeśli chodzi o lokaty złotowe, to w Polsce nie mamy się o co obawiać. Bardzo niska inflacja powoduje, że zawsze zarobimy na tej lokacie (oprocentowanie jest wyższe od tempa inflacji). Jest to dużo bezpieczniejsza forma lokowania pieniędzy.
Z powyższych danych wynika, że największy zysk osiągnęlibyśmy wkładając nasze oszczędności na lokatę dolarową na 6 miesięcy. Natomiast najwięcej stracilibyśmy zakładając lokatę w walucie euro na okres 3 miesięcy. Trzeba jednak pamiętać, że nie są to dane realne. Obecnie lokowanie w euro jest opłacalne, ponieważ ostatnimi czasy waluta ta stale rośnie, a inflacja w kraju pozostaje bez zmian na bardzo niskim poziomie. Jeśli chodzi o lokaty w dolarach, to tu sytuacja jest bardziej ryzykowna. Przez obecne konflikty zbrojne oraz prawdopodobieństwo ataków terrorystycznych, na rynku dolara zachodzą wahania.
REALNE STOPY PROCENTOWE DEPOZYTÓW ZŁOTOWYCH I DEWIZOWYCH W BANKU BGŻ W LUTYM 2003
3
POLITECHNIKA KOSZALIŃSKA
Wydział Ekonomii i Zarządzania
Koszalin 2003


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
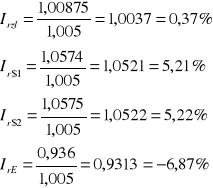
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
RF wyk Rosiński, Archiwum, Semestr VIII, Przedmioty ogólne, Rynki finansowe
MSG Garbe, Archiwum, Semestr VIII, Przedmioty ogólne, Międzynarodowe stosunki gospodarcze
KZP wyk2 Paradygmaty, Archiwum, Semestr VIII, Ekonomia menedżerska
KZP wyk7 Organizacja ucząca się, Archiwum, Semestr VIII, Ekonomia menedżerska
Jankowiak, Archiwum, Semestr VIII, Ekonomia menedżerska
KZP wyk5 Benchmarking, Archiwum, Semestr VIII, Ekonomia menedżerska
KZP wyk3 Outsourcing, Archiwum, Semestr VIII, Ekonomia menedżerska
KZP wyk9 Lean management, Archiwum, Semestr VIII, Ekonomia menedżerska
Test- zarzadzanie finansami spółek, Archiwum, Semestr VIII, Finanse i Rachunkowość
KZP wyk4 Reengineering, Archiwum, Semestr VIII, Ekonomia menedżerska
Filozofia karta przedm, semestr VIII, Semestr VIII, VIII semestr, Filozofia, Materiały od wykładowcy
SYLABUS PRZEDMIOTU.do rynek kapitalowy i finansowy, Ekonomia UWr WPAIE 2010-2013, Semestr V, Rynki f
Zagadnienia z przedmiotu Geologia i ochrona złóż 09 10, Ochrona Środowiska studia, 4 rok (2009-2010
kjp-Karta Przedmiotu, Edukacja, studia, Semestr VIII, Kultura Języka Polskiego, CD1 - 2006 KJP-1 INF
Wybierz, Edukacja, studia, Semestr VIII, Kultura Języka Polskiego, CD1 - 2006 KJP-1 INFORMATYKA, KJP
sciaga tomczewski, semestr VIII, Semestr VIII, VIII semestr, Wprowadzenie do telekominikacji
rodzaje', Edukacja, studia, Semestr VIII, Kultura Języka Polskiego, CD1 - 2006 KJP-1 INFORMATYKA, KJ
zarzadzanie strategiczne kol1, Archiwum, Semestr IX
1 Ostre choroby zakaźne wieku dziecięcego, Medycyna, Pediatria, semestr VIII, tydzień II
więcej podobnych podstron