Oligopol

(bardzo dokładna prezentacja w podręczniku)

1. Firmy współzależne i gry o sumie niezerowej

2. Model Cournot'a

3. Domniemane zmiany

Konkurencja monopolistyczna

4. Równowaga w LR w konkurencji monopolistycznej

5. Równowaga w LR i doskonała konkurencja

*

Oligopol

Większość rynków nie jest ani monopolem, ani doskonałą konkurencją, ale ich struktury znajdują się gdzieś pomiędzy tymi biegunami. Nawet monopolista napotyka na konkurencję ze strony producentów substytutów. Na typowym rynku działa więcej niż jeden producent podobnego dobra. Producenci nie są cenobiorcami. Każda firma napotyka więc opadającą krzywą popytu, a wiec posiada pewną dozę siły monopolistycznej. Tradycyjnie oligopol i konkurencja monopolistyczna analizowane były dzięki konstruowaniu serii specyficznych modeli dla poszczególnych rynków. Nowocześniejsze podejście polega na wyborze strategii przez firmy.

Firmy współzależne i gry o sumie niezerowej: Gry kooperacyjne i kartele

Gry kooperacyjne - wspólnym celem jest maksymalizacja wspólnego zysku i jego dystrybucja w taki sposób, że sytuacja żadnego z graczy nie pogarsza się w porównaniu do sytuacji, w której firma nie współpracuje.

Gry niekooperacyjne - gracze maksymalizują korzyści bez kooperacji.

Zawsze, gdy istnieje możliwość ustalenia cen - wielkości produkcji maksymalizujących zysk monopolistyczny, to otwiera się możliwość prowadzenia gry kooperacyjnej. ALE: Aby uzyskać ten zysk firmy muszą umówić się, że nie będą produkować więcej niż wynosi wielkość produkcji monopolu i ustanowią monopolistyczną cenę. Taka współpraca to zawiązanie kartelu.

Jeden ze sposobów funkcjonowania kartelu (działanie jak monopol i dystrybucja zysku) wymaga wyznaczenia popytu dla całego przemysłu i określenia wielkości produkcji każdej firmy aby MR_przemysł = MC_{każda firma}. Wspólne zyski:

Warunki pierwszego rzędu:

dla wszystkich j,

gdzie X jest sumą wszystkich x_j.

Czyli: MR = MC_j dla wszystkich j ⇒ W punkcie maksymalizującym wspólny zysk każda firma produkuje tyle, że MR_przemysł związany z całkowitą wielkością produkcji równa się MC_firma związane z wielkością produkcji tej firmy. Jest to sprzeczne z zasadą maxπ firmy (MR_firma = MC_firma)

Przykład: Powstanie OPEC:

Każda firma zaczyna od konkurencyjnej wielkości produkcji sprzedawanej po konkurencyjnej cenie. Wiadomo, że wielkość produkcji w monopolu jest mniejsza niż w konkurencji doskonałej, a cena jest wyższa. Aby więc przemysł konkurencyjny zawiązał kartel każda z firm musi zgodzić się na zmniejszenie produkcji, żeby suma równała się produkcji monopolistycznej. Po ograniczeniu produkcji cena wzrośnie. Aby wszystkie firmy zgodziły się, to każda z nich musi osiągnąć wyższy zysk niż przed zawiązaniem kartelu. Różne firmy mają różne funkcje kosztów.

Jeżeli firmy obserwują wielkość produkcji i mogą sądownie wymusić restrykcje ilościowe, to kooperacyjny kartel będzie stabilny. Np. w Japonii i Niemczech kartele są legalne, a w USA - nie. Pomimo że OPEC nie jest nielegalny, to i tak nie może wymuszać porozumień dotyczących wielkości produkcji.

Oszukiwanie

Istnieje silna pokusa do oszukiwania, gdyż każda firma zyskuje na zwiększaniu wielkości produkcji. Jeśli więc kartel nie ma możliwości obserwowania wielkości produkcji i wymuszania przestrzegania ograniczeń produkcji, to wszystkie firmy będą miały bodziec do oszukiwania.

Rys. 16.2: w punkcie (x*, p*)cały przemysł maksymalizuje wspólny zysk (π*). Każda z firm uważa, że jeżeli zwiększy troszeczkę wielkość produkcji (Δx), to jej zysk zwiększy się nawet jeśli cena rynkowa nieznacznie obniży się do p¹_x. Jeśli dwie firmy produkują tyle samo maksymalizując wspólny zysk, to firma B straci zacienioną część zysku, gdy zwiększy produkcję i doprowadzi do obniżki ceny, ale otrzyma część zysku zacienionego wywołanego zwiększeniem produkcji. Przy małych wzrostach produkcji, zwiększanie zysku przewyższa jego straty. Istnieje optymalne zwiększenie produkcji przez B (maksymalizujące wzrost zysku), jeśli A dotrzymuje umowy.

Rys. 16.3: Obie firmy zwiększają produkcję o Δx Całkowity wzrost wielkości produkcji: 2Δx, cena obniża się do p²_x. Ponieważ cena spada bardziej niż, gdy tylko firma B oszukiwała, to teraz ta firma traci więcej niż zyskuje.

Przykład:

krzywa popytu rynkowego: p_x = 20 - x

zał.: MC = 0; każda z firm zgodziła się produkować połowę wielkości produkcji monopolu i otrzymywać połowę zysku monopolu. Aby znaleźć produkcję monopolu wyznaczamy funkcję zysku: π_m = 20x - x² i warunek konieczny:
. Rozwiązanie: x* = 10; p_x*= 10; π_m* = 100. Każda z firm produkuje 5 jednostek i osiąga zysk = 50 przy cenie wynoszącej 10. Firma 1 oszukuje i produkuje 6 jednostek. Jeżeli firma 2 w dalszym ciągu produkuje 5 jednostek, to produkcja rynkowa = 11, a cena spadnie do 9. Przy cenie = 9 i zerowych kosztach, firma 1 ma zysk = 54 (6 × 9), czyli więcej niż 50, a firma 2 ma zysk 45 (5 × 9), czyli mniej niż 50. Jeżeli obie firmy będą produkować po 6 jednostek, to całkowita produkcja rośnie do 12, cena spada do 8 i każda osiąga zysk równy 48.

Duopol Cournot'a

Zał. 1: Liniowy popyt

Zał. 2: MC = 0

Zał. 3: Produkt homogeniczny

Zał. 4: Firmy nie uczą się

Zaczynamy od monopolu i potem pozwolimy drugiej firmie wejść na rynek.

Funkcja popytu: x = a - (a/b)p_x.

Rys. 16.6: monopolista maxπ: MC = 0 = MR ⇒ (x*, p_x*) = ((1/2)a; (1/2)b). Druga firma zakłada, że monopolista będzie produkować ½a. Wchodząca firma traktuje pozostałe ½a krzywej popytu jako własny popyt i zachowuje się jak monopolista w tym segmencie - rys. 16.7. Oryginalny monopolista produkuje ½a pozostawiając niższą, prawą część swej krzywej popytu niezaspokojoną. Firma wchodząca traktuje tę niższą część jako swą „rezydualną”.

Wielkość produkcji maksymalizująca zysk dla dolnej części popytu:

½ (a - ½ a) = ¼ a. Ale jeżeli firma 2 wytwarza ¼ a, to firma 1 nie jest monopolistą, czyli produkcja: ½ a nie maksymalizuje zysku. Firma 1 traktuje decyzje dotyczące wielkości produkcji firmy 2 (¼ a) jako stałą i przyjmuje pozostałą część krzywej popytu, czyli wielkość produkcji maksymalizująca zysk wynosi: ½ (a - ½ a) = (3/8)a. Ten proces dostosowawczy trwa aż żadna z firm nie ma motywacji do zmiany wielkości produkcji. Jeżeli każda z firm oferuje (1/3)a, to firma 2 oferuje: ½ (a - (1/3)a) = (1/3)a, a firma 1 oferuje: ½ (a - (1/3)a) = (1/3)a. Wielkość produkcji w równowadze: x = (1/3)a + (1/3)a = (2/3)a i cena w równowadze wynosi: p_x = b - (b/a) (2/3)a = (1/3)b. Rys. 16.8

Funkcje reakcji i równowaga

Odwrotny popyt: p_x = b - (b/a)(x₁ + x₂)

Mnożąc powyższe równanie przez x₁ otrzymujemy zyski firmy 1: π₁ = [b - (b/a)(x₁ + x₂)]x₁ . Różniczkujemy względem x₁ i przyrównujemy do 0 aby określić decyzje maksymalizujące zysk:
⇒ x₁ = ½ (a - x₂): jest to funkcja reakcji firmy 1 opisująca wielkość jej produkcji jako funkcję wielkości produkcji konkurenta. Analogicznie wyprowadzamy funkcję reakcji firmy 2:

π₂ = [b - (b/a)(x₁ + x₂)]x₂ ⇒
⇒

x₂ = ½ (a - x₁).

Jest to słaba równowaga Nash'a w grze niekooperacyjnej.

Rozwiązanie: x₂ = ½ (a - ½ (a - x₂)) = ½ a - ¼ a + ¼ x₂ ⇒

x₂ = (1/3)a ⇒ x₁ = ½ (a - (1/3)a) = (1/3)a (rys. 16.9)

Rozszerzenie dla n firm:

Zał.: są 3 firmy i dwie z nich oferują ¼ a. Trzecia firma maxπ dla pozostałej części krzywej popytu:

x₃ = ½ (a - ¼ a - ¼ a) = ¼ a.

Pierwsze dwie firmy odpowiadają tym samym:

x₁ = x₂ = ½ (a - ¼ a - ¼ a) = ¼ a.

Przy n firmach, każda z nich oferuje:
, a więc każda inna oferuje: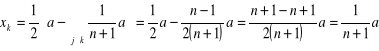
i to są wielkości produkcji w równowadze. Sumowanie po j daje wielkość dla rynku:
. Cena wynosi:
.

Pozwólmy wchodzić nowym firmom i określmy graniczne wielkości ceny i wielkości produkcji:
i
. Jeżeli więc n dąży do nieskończoności, to wielkość produkcji dąży do a cena zaś do 0, czyli równa się MC (cena doskonale konkurencyjna). Model Cournot'a z możliwością wejścia staje się modelem doskonałej konkurencji przy ilości firm dążącej do nieskończoności.

Rozszerzenie dla dodatnich MC

Zał.: MC stałe i dodatnie. (Rys. 16.10) Jeżeli LRMC = c, to wielkość produkcji w doskonałej konkurencji wyniesie d. Możemy wyprowadzić równowagę Cournot'a traktując linię MC jako oś odciętych w modelu z MC = 0. Czyli d jest punktem przecięcia wielkości produkcji, a wielkość produkcji w równowadze duopolu wyniesie: (1/3)d przy cenie:

c + (1/3)(b - c). Uogólniając:
i
.

Domniemane zmiany

Założenie, że działania konkurentów są stałe jest nierealistyczne. Jest ono nieprawdziwe dla wszystkich punktów poza równowagą. Zmiany wielkości produkcji następują aż równowaga zostaje osiągnięta - menadżerowie oczekują domniemanych zmian wielkości produkcji u konkurentów.

Funkcje reakcji z domniemanymi zmianami

Zacznijmy od sytuacji, w której firmy przewidują jeden ruch do przodu. Możemy wyrazić oczekiwania firmy 1 w postaci funkcji: x₂ = x₂(x₁), a firmy 2: x₁ = x₁(x₂).

Przy liniowej funkcji popytu i stałych MC funkcja zysku firmy 1: π₁ = {b - (b/a)[x₁ + x₂(x₁)]}x₁ - cx₁

Warunek pierwszego rzędu:

.

Po uporządkowaniu wyrażeń funkcja reakcji firmy 1 uwzględniająca domniemane zmiany przyjmuje postać:

.

Funkcja reakcji firmy 2 jest symetryczna:

.

Rozważmy trzy możliwe założenia dotyczące domniemanych zmian czynionych przez firmę.

Wspólne domniemane zmiany

Po pierwsze, możemy przyjąć, że firmy będą przestrzegać ograniczeń ilościowych i osiągną sytuację monopolu. Z tego wynika domniemana zmiana +1 dla każdej firmy. Wstawiając +1 za pochodne w równaniach funkcji reakcji otrzymujemy:

i
.

Aby wykazać, że te funkcje reakcji prowadzą do rozwiązania w postaci monopolu najpierw znajdujemy rozwiązanie dla monopolu dzięki maksymalizacji funkcji zysku monopolu zakładając: x₁ + x₂ = x_m:

⇒

Teraz dodajmy funkcje reakcji i rozwiążmy dla wielkości produkcji w równowadze:

⇒

Doskonale konkurencyjne domniemane zmiany

Drugim skrajnym przypadkiem jest przyjęcie założenia, że jeżeli firma zmniejszy wielkość produkcji o jednostkę, to inna firma zwiększy produkcję o jednostkę aby zniwelować różnicę. Z tego założenia wynika, że każda pochodna = -1:

.

Wstawiając -1 za pochodne w równaniach funkcji reakcji otrzymujemy:

i
.

Wykażemy, że przy takich funkcjach reakcji obie firmy wytworzą wielkość produkcji dla rynku doskonale konkurencyjnego. Aby określić tę wielkość produkcji zrównujemy cenę z MC:
⇒
.

Teraz znajdujemy wielkość produkcji obu firm z domniemanymi zmianami = -1:

⇒
.

Z równań wynika, że nie jest określona wielkość produkcji poszczególnych firm, pomimo że określona jest wielkość produkcji przemysłu. Jest to analogia do równowagi w LR w konkurencji doskonałej ze stałymi korzyściami skali. Ponieważ każda wielkość produkcji kosztuje w przeliczeniu na jednostkę tyle samo w LR, czyli nie ma zysków, to firmom jest obojętne, w jaki sposób alokowana jest produkcja.

Domniemane zmiany Cournot'a

Pośrednie założenie dotyczące domniemanych zmian jest dokonywane w modelu Cournot'a, gdzie przyjmuje się, że każda firma traktuje wielkość produkcji konkurenta jako stałą. Jest to założenie głoszące, że zerowych domniemanych zmianach:
. Wstawiając 0 za pochodne w równaniach funkcji reakcji otrzymujemy:
i
. Po dodaniu tych wielkości produkcji:

⇒
.

Wielkość produkcji w oligopolu wynosi 2/3 wielkości produkcji w doskonałej konkurencji.

Przy domniemanych zmianach od +1 do -1 można otrzymać doskonałe porozumienie - najwyższa cena i najmniejsza wielkość produkcji, duopol Cournot'a lub doskonałą konkurencję - najniższa cena i największa produkcja.

Konkurencja monopolistyczna

Istnienie zróżnicowanych produktów i niedoskonałej informacji u konsumentów oznacza korzyści zarówno dla konsumentów, jak i dla producentów z reklamy. Konsumenci wiedzą więcej, czyli łatwiej wybrać im koszyk maksymalizujący ich użyteczność. Firmy mogą sprzedać więcej dzięki informacjom posiadanym przez konsumentów. Dzięki reklamie lub dzięki posiadanym korzyściom skali w konkurencji monopolistycznej firmy wytwarzają zróżnicowany produkt przy rosnących korzyściach skali lub przy kosztach przeciętnych w kształcie U w LR. Każda firma jest monopolem dla swojego produktu, ale popyty na produkty poszczególnych firm są względnie elastyczne, czyli istnieje wiele potencjalnych substytutów spośród nieco zróżnicowanych produktów oferowanych przez innych producentów. Dlatego problem decyzyjny każdej z firm można rozwiązywać w sposób zbliżony do monopolu. Przyjmując, że firma zna popyt, maksymalizuje ona zyski wybierając wielkość produkcji i wysokość ceny zrównując MC i MR - rys. 16.12.

Równowaga w LR w konkurencji monopolistycznej

Zyski osiągane przez firmy zachęcają potencjalnych konkurentów do wejścia na rynek. Ich oferta przyciąga konsumentów, którzy po części mogą zrezygnować z dotychczasowej oferty, co prowadzi do przesunięcia na lewo krzywych popytu firm działających na rynku. Ponadto krzywe popytu mogą stać się bardziej elastyczne - rys. 16.13.

Przy wolnym wejściu na rynek, firmy będą wchodzić aż skończy się możliwość osiągania zysku. Jak w konkurencji doskonałej, gdzie w LR zysk = 0. W konkurencji monopolistycznej p > MC i p > minLRAC w równowadze w LR.

Dzieje się tak, gdyż każda firma napotyka opadającą krzywą popytu i posiada pewną siłę monopolistyczną pomimo wyeliminowania zysku - rys. 16.14.

Równowaga w LR i doskonała konkurencja

Co się stanie, gdy ilość firm dąży do nieskończoności? W modelu Cournota pokazaliśmy, że rozwiązanie dąży do konkurencji doskonałej. W modelu konkurencji monopolistycznej można podać ten sam argument dla kosztów w LR w kształcie U i gdy krzywe popytu stają się coraz bardziej elastyczne przy wchodzeniu nowych firm. Jeżeli bowiem krzywe popytu stają się coraz bardziej elastyczne, to w końcu żadna firma nie będzie miała siły rynkowej, jak w doskonałej konkurencji - rys. 16.15. Firma j-ta jest cenobiorcą, a jej krzywa popytu jest doskonale elastyczna przy cenie rynkowej.

Model konkurencji monopolistycznej pozwala sformułować kilka ważnych spostrzeżeń:

1. Jeżeli w równowadze w LR cena jest wyższa od ceny z równowagi doskonale konkurencyjnej w LR, to różnica między ceną i MC pokazuje długookresową cenę, jaką płacimy za zróżnicowanie produktów.

2. Zbieżność w granicy pokazuje siłę wejść i konkurencyjności eliminujących nieefektywność nawet wtedy, gdy firma ma pewną siłę monopolistyczną.

3. Równowaga konkurencji niedoskonałej jest nieefektywna w tym sensie, że p ≠ MC i p > minLRAC. Jeżeli jednak produkty zaczynają być homogeniczne, to siły rynkowe eliminują i ten ślad nieefektywności.

Oligopol - zadania

Przykład: max π przy zmowie

Oligopoliści mogą uzgodnić wspólne działanie dążąc do max wspólnego zysku i dzięki temu zwiększając oczekiwane zyski każdej z firm. Określą oni wspólną cenę, wielkość produkcji każdej z firm i sposób podziału zysku. Jest to kartel.

Dla uproszczenia: duopol z homogenicznym produktem.

q₁ - wielkość produkcji 1. firmy;

q₂ - wielkość produkcji 2. firmy;

q₁ + q₂ = q - wielkość produkcji przemysłu;

C₁(q₁) - koszty 1. firmy;

C₂(q₂) - koszty 2. firmy;

C₁(q₁) + C₂(q₂) = C - koszty przemysłu;

p = h(q_d) - popyt na produkt.

TR = pq = h(q)q = R(q) = R(q₁ + q₂).

Funkcja zysku przemysłu:

π = TR - C = R(q₁ + q₂) - C₁(q₁) - C₂(q₂)

Aby znaleźć wielkość produkcji max π:

i

lub:
i
czyli MC = MR dla każdej firmy.

Widać, że MR przemysłu jednostki produktu jest taki sam niezależnie, która firma ją wyprodukowała:
, czyli warunki konieczne można zapisać:

.

(Trzeba też sprawdzić warunki wystarczające i możliwość istnienia rozwiązań brzegowych.)

Przykład: max π przy przywództwie cenowym firmy dominującej

Oligopol z k firmami sprzedającymi produkt homogeniczny. Jedna z firm jest przywódcą cenowym: q₁ to wielkość jej produkcji, a q_i to wielkość produkcji i-tej firmy, gdzie i = 2, 3, ...., k. Produkcja rynku: q = q₁ + q₂ + .... + q_k =
. Popyt rynkowy: q_d = f(p).

Przywódca cenowy wyznacza cenę przyjmowaną przez pozostałe firmy, które dostosowują wielkość produkcji w celu maxπ. Wszystkie firmy, oprócz lidera, zachowują się jak w konkurencji doskonałej. Dla każdej z nich: π_i = pq_i - C_i(q_i). Aby maxπ pochodną tej funkcji przyrównujemy do zera traktując cenę jako stałą:

⇒
.

Jest to warunek konieczny maxπ dla każdej firmy oprócz lidera. Firmy te zrównują więc cenę wyznaczoną przez lidera ze swoimi MC wyznaczając wielkość produkcji przyjmując, że warunki drugiego rzędu są spełnione i nie ma rozwiązań brzegowych. Jeżeli cena wyznaczana przez lidera zmienia się, to również zmienia się wielkość produkcji max π każdej z firm: q_i = g_i(p).

Przywódca cenowy oblicza wielkość produkcji wytwarzaną przez wszystkie pozostałe firmy przy każdej cenie. Potem wstawia te wartości q_i do funkcji popytu rynkowego w celu określenia funkcji popytu na własny produkt. Popyt rynkowy opisuje równanie: q_d = f(p), gdzie q_d odnosi się do wszystkich firm, czyli: q₁ + q₂ + .... + q_k = f(p) lub q₁ = f(p) -
.

Ale: q_i = g_i(p), dlatego: q₁ = f(p) -
.

Lider określi więc swoją funkcję TR rozwiązując równanie q₁ = f(p) -
. Zna on funkcję kosztów od q₁ i wyznacza zysk. Warunek konieczny: MC = MR.

Przykład: max π przy stałych udziałach na rynku

Zdarza się, że wszyscy sprzedający na rynku oligopolistycznym pozwalają jednej firmie na przywództwo cenowe, pod warunkiem, że mogą zachować swoje udziały na rynku. Jeżeli lider zmienia cenę, to inne firmy reagują zmieniając swoje ceny aby zachować swój udział na rynku. Dla dwóch firm: q₁ + q₂ = q: wielkość produkcji rynkowej. Firma 1: przywódca cenowy, przy ustalonym podziale rynku. Udział firmy 2: to K, czyli: K = q₂/( q₁ + q₂). Rozwiązując dla q₂: q₂ = K(q₁ + q₂) = Kq₁ + Kq₂ ⇒ q₂ = Kq₁/(1 - K).

Firmy produkują homogeniczny produkt, na który popyt opisuje równanie: p = f(q) lub: p = f(q₁ + q₂). Funkcja zysku firmy 1: π₁ = TR₁ - C₁ = pq₁ - C₁(q₁) = q₁f(q₁ + q₂) - C₁(q₁). Wstawiając wartość q₂ otrzymujemy:

π₁ = q₁f(q₁ + Kq₁/(1 - K)) - C₁(q₁), czyli zysk firmy 1 można wyrazić jako funkcję q₁. Aby ją max różniczkujemy ją względem q₁ i przyrównujemy do zera. Otrzymujemy więc wartość q₁ i q₂ można obliczyć z q₂ = Kq₁/(1 - K).

W przypadku produktu zróżnicowanego popyty każdej z firm opisują równania: p₁ = h₁(q₁, q₂) i p₂ = h₂(q₁, q₂). Funkcja zysku firmy 1: π₁ = TR₁ - C₁ = pq₁ - C₁(q₁) = q₁h₁(q₁ , q₂) - C₁(q₁). Po wstawieniu wartości q₂ (z q₂ = Kq₁/(1 - K)) mamy:

π = q₁h₁(q₁ , Kq₁/(1 - K)) - C₁(q₁). Ponownie zysk firmy 1 jest funkcją wyłącznie q₁. Można wyznaczyć jego max różniczkując funkcję względem q₁ i przyrównując ją do zera. Otrzymamy więc q₁ a q₂ wyznaczamy z q₂ = Kq₁/(1 - K).

---