13. W*aściwości elektryczne i cieplne

Polimery na ogół są dielektrykami wskutek specyfiki ich budowy chemicznej. Przewodność elektryczną wykazują polimery specjalne o budowie biegunowej powodującej stały ładunek w obiętości lub napełnione przewodnikiem minieralnym.

13.1. Przenikalność dielektryczna i współczynnik stratności dielektrycznej

Zdolność do przewodzenia prądu pod działaniem natężenia pola elektrycznego przyłożonego do próbki polimeru nazywa się przewodnością właściwą elektryczną. Dzieli się ona na jonową, molowa i elektronową. Sumaryczna wartość przewodności wynosi:

, Ω^-1∙m^-1

gdzie: n_i - liczba nośników ładunku;

q_i - ładunek nośnika;

χ_i - ruchliwość nośnika.

Rozróżnia się przewodność obiętościową (γ_ν) i powierchniową (γ_s). Wszystki materiały można podzielić na przewodniki, półprzewodniki i dielektryki (izola­tory) względem wartości przewodności elektrycznej właściwej (γ_ν, Ω^-1∙m^-1) [25]:

Przewodniki	> 10 ^2
Półprzewodniki	= 10^-3÷10^-9
Dielektryki	< 10^-9

Wartości przewodności elektrycznej objętościowej (γ_ν) i powierzchniowej (γ_s) dla niektórych polimerów są nestępujące [25]:

	γν, Ω^-1∙m^-1	γs, Ω^-1
Poli(chlorek winylu)	10^-12÷10^-14	10^-12÷10^-13
Poli(tereftalan etylenu)	10^-13÷10^-14	10^-14÷10^-15
Polietylen	10^-14÷10^-15	10^-16÷10^-17
Polistyren	10^-14÷10^-16	10^-16÷10^-17

Napełniacze takie jak sadza, grafit, metale powodują zwiększenie przewodności polimeru. Natomiast obecność plastyfikatora zmniejsza wpływ napełniaczy.

Przewodność w polimerze odbywa się za pomocą jonów lub dipoli znajdujących się w strukturze makrocząsteczki. Jeśli liczba jonów swobodnych w polimerze jest zbyt mała, przewodność jest również małą.

Wielkość odwrotną do γ_ν nazywa się rezystywnością, która dzeli się na skrośną lub objętościową (ρ_ν=1/γ_ν w Ω⋅m) i powierzchniową (ρ_s w Ω). Rezystywność - jest to opór elektryczny materiału.

W warunkach oddziaływania na polimery pola elektrycznego zewnętrznego w polimerze pojawia się moment elektryczny - występuje polaryzacja dielektryku (P), która składa się z dwóch części - deformacyjnej (P_def) i orientacyjnej (P_or). P_def - polaryzacja uwarunkowana odkształceniem osłony elektronowej, przesunięciem jąder atomowych lub jonów; P_or - polaryzacja spowodowana orientacją swobodnych jonów lub stałych dipoli o stałych momentach dipolowych. Wektor polaryzacji
powiązany jest z natężeniem pola elektrycznego E_n przez zależność [25]:

= ε₀ ∙ H ∙ d ∙ E_n

gdzie: ε₀ - stała elektryczna, równa się 8,854 F/m;

H_d - współczynnik nazywany reproduktywnością dielektryczną;

E_n - natężenie elektryczne.

Wielkość H_d można związać z przenikalnością elektryczną rzeczycistą (ε′) polimeru w sposób następujący:

gdzie: α - zdolność do polaryzacji;

n_d - liczba dipoli orientowanych.

Polaryzacja deformacyjna odbywa się zbyt szybko (10^-14÷10^-12 s) natomiast polaryzacja orientacyjna przebiega z opóźnieniem w czasie (τ_op). Opóźnienie uwarunkowane jest małą ruchliwością dipoli wskutek przeszkód przestrzennych (sterycznych) w ciale stałem, w którym znajduje się polimer. Opóźnienie procesów polaryzacji orientacyjnej nosi nazwę relaksacji dielektrycznej (w czasie τ).

Przeszkody przestrzenne powodują rozpraszanie części energii elektrycznej w objętości polimeru, są to straty dielektryczne i stanowią pozorną część przenikalności (iε′′).

Na skutek tego przenikalność dielektryczną polimeru przedstawia się w nastę­pujący sposób:

Straty dielektryczne równają się wartości ciepła, powstającego w objętości jednostkowej pod działaniem prądu przepływającego przez polimer. W warunkach doskonałych kąt pomiędzy ε′ a ε′′ wynosi 90^o.

W warunkach rzeczywistych kiedy występuja straty, kąt ten maleje o wartość δ (kąt strat dielektrycznych). Tangens kąta δ nazywa się współczynnikiem strat dielektrycznych i wyraża się go wzorem:

tgδ = ε′′/ε′

Przenikalność dielektryczna jest umownie przyjęta jako stosunek pojemności (C) kondensatora, w którym przestrzeń między i wokół elektrod wypełniona jest polimerem a pojemnością (C₀) kondensatora z elektrodami umieszczonymi w próżni lub w suchym powietrzu [22]:

lub

gdzie: C₀ i C_p - pojemności kondensatora w próżni i w suchym powietrzu w warunkach normalnych.

W przypadku kondensatora płaskiego przewodność G wyznacza się ze wzoru [24]:

a

gdzie: 2πf =ω - pulsacja prądu;

R - rezystywność.

Wtedy tgδ można okreslić jako:

Im mniejsza wartość tgδ i ε tym polimer jest lepszym dielektrykiem (izolatorem). Najlepszymi dielektrykami są polimery niebiegunowe - t.j.: polietylen, polistyren i polipropylen. Ze wzrostem biegunowości, właściwości dielekryczne pogorszają się. Wybrane wartośći tgδ i ε dla polimerów zestawiono w tabeli 13.1.

Tabela 13.1

Właściwości dielektryczne niektórych polimerów [35,37]

Polimer	ρv, Ω*cm	Epr, przy 50 Hz, kV/mm	ε, przy		tgσ*10^2, przy
						50 Hz	10^6Hz	50 Hz	10^6Hz
PS	10^17	20÷25	-	2,6÷2,8	-	4⋅10^-2
PC	(0,5÷1)⋅10^17	20÷30	3,0÷3,1	2,9÷3,0	0,2	0,8
PMMA	10^12÷10^13	13÷14	3,0	3,6	0,1	1,0
PVC plast.	10^10÷10^14	26÷28	−	4,2÷5,0	−	0,1
PVC	10^1^4÷10^1^6	26÷60	−	3,1÷3,4	−	1,5÷1,8
PE-LD	10^1^7	40÷45	−	2,4	−	(2÷4)⋅10^-2
PE-HD	10^1^7÷10^1^8	40÷45	−	2,2÷2,3	−	(2÷3)⋅10^-2
PP	10^1^6÷10^1^7	30		2,4	−	5,0⋅10^-2
PA-6	10^14÷10^15	20÷28	4,0÷5,0	3,6÷4,0	0,2÷0,4	2,0-3,0
PA-66	10^14÷10^15	25	3,6	4,0	2,0	4,0
POM	10^1^4÷10^1^5	21÷24	3,7	3,7	2,0÷4,0	0,5÷0,9
PET	10^16÷10^17	12÷17	−	3,3÷3,5	−	1,0÷2,0

Dla polimerów niebiegunowych wymienione wielkości nie zależą od częstotliwości pola zewnętrznego i jego wielkości. Natomiast dla polimerów biegunowych występuje zależność ε′ i ε′′ od temperatury i częstotoliwości pola elektrycznego. Zależność ta uwarunkowana jest procesem relaksacyjnym, który dzieli się na dipolowo-segmentalny (DS lub α-przejście) i dipolowo-grupowy (DG - lub β-przejście). Przejście DS spowodowane jest ruchliwością segmentalną i ujawnia się w temperaturze T≥T_g, a w przypadku dipolowo-grupowego - przejście ujawnia się w obszarze T<T_g i spowodowane jest procesami orientacji biegunowych grup bocznych.

Energia aktywacji DS nie przekraca 5÷15 kJ/mol, a DG - jest znacznie większą i wynosi 130÷590 kJ/mol.

Zależność tg δ i ε od temperatury i częstotliwości ω ma charakter ekstremalny. Zależność tą ilustruje rys. 13.1.

Według teorii Debye'a maksimum na krzywej zależności ε od ω pojawia się w warunkach spełniających zależność:

gdzie: α - współczynnik, który zależy od zakresu czasu relaksacji (α=0, gdy istnieje jeden czas relaksacji zbliżający się do nieskończoności; i w przypadku dużej ilości czasów relaksacji poszczególnych elementów α daży do 1);

ε₀ i ε_∞ - przenikalność dielektryczna przy ω₁→0 i ω→∞, odpowiednio.

Przenikalność dielektryczna i straty dielektryczne zależą od budowy chemicznej polimeru, jego ciężaru cząsteczkowego, struktury nadcząsteczkowej i od rodzaju domieszek.

Na przykład, dla polimerów biegunowych, ze wzrostem polarności wzrasta czas relaksacji, wskutek czego zwiększa się temperatura, w której pojawia się maksimum procesów DS i DG, wówczas rośnie tgδ i ε″.

Wartość tgδ wrasta w przypadkach zwiększenia zarówno polarności grup biegunowych, ich objętości, sił oddziaływania międzyczasteczkowego jak i przy zwiększeniu stopnia krystaliczności (gdy ruchliwość segmentów w krystalitach nie całkowicie zahamowana). W przypadkach zmniejszenia się ruchliwości grup i segmentów przy krystalizacji spostrzega się zmniejszenie tgδ i ε″.

Ze wzrostem rozgałęzienia makrocząsteczek lub stopnia usieciowania polimerów amorficznych, wartości ε′ i ε′′ maleją w stanie wysokoelastycznym i rosną w stanie szklistym. Obecność plastyfikatora powoduje wzrost tgδ i ε′ polimeru i obniżenie temperatury wystąpienie maksimum na zależności tgδ-T.

Zależność wymienionych właściwości od struktury polimeru, jego składu fazowego pozwala ustalać skład kopolimerów, strukturę polimerów, czas relaksacji naprężeń (ω_maks⋅τ=1), ciężar cząsteczkowy, stan fazowy mieszanin polimerowych i inne.

13.1.1. Wytrzymałość elektryczna i elektryzacja statyczna

Oprócz powyżej wymienionych właściwości, ważne znaczenie dla dielektryka ma też wytrzymałość elektryczna - jest to zakres napięcia pola zewnętrznego, w którym gwałtownie rośnie przepływ ładunków elektrycznych na wskoś izolatora. Taki przypadek nazywa się przebiciem elektrycznym, a napięcie, w którym zachodzi przebicie nazywa się napięciem przebicia. Dla większości polimerów zakres tego napięcia wynosi E_pr = 10⁵÷10⁶ kV/m.

Wytrzymałość elektryczna (E_pr) jest stosunkiem napięcia elektrycznego (U_p) pod działaniem którego następuje przebicie do odległości h_p między elektrodami (grubości próbki polimeru):

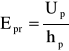
Po przekroczeniu E_pr polimer staje przewodnikiem. Wyróżnia się następujące rodzaje przewodności: elektronową, cieplną i gazową. Przewodność elektronowa przejawia się w zakresie temperatur niższych za T_g dla polimerów amorficznych lub T_m gdy polimer krystaliczny. Przewodność cieplna zachodzi przy nagrzewaniu polimeru w temperaturzę przewyższającej T_g lub T_m co powoduje gwałtowny wzrost gęstkości prądu skrośnego płyniącego przez próbkę i, odpowiednio, zmniejsza się wytrzymałość elektryczna.

Przebicie elektryczne cieplne może powstawać, gdy następuje nagrzewanie się polimeru pod działaniem pola elektrycznego. Przewodność gazowa powstaje w warunkach tworzenia się gazu jonowego w przestrzeni międzycząsteczkowej.

Dielektryki polimerowe różnią się zdolnością akumulowania i utrzymania ładunku elektrycznego powierzchniowego. Zjawisko to nazywa się elektryzacją statyczną, spowodowaną różną szybkością pojawiania się i zaniku ładunku statycznego. Gęstość powierzchniowa ładunku (σ_e) równa się [25]:

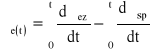
gdzie: t - czas akumulacji;

ez - oznacza akumulowania ładunku;

sp - oznacza zanik ładunku statycznego.

Zanik ładunku statycznego odbywa się wskutek oddziaływań z grupami lub z czą­steczkami biegunowymi w polimerze i w powietrzu. Z tego wynika, że polimery apolarne elektryzują się w stopniu większym niż biegunowe.

13.2. Właściwości cieplne

Fizyczne właściwości cieplne należy traktować jak reakcję polimeru na działanie zewnętrznego pola cieplnego. Reakcje te są specyficzne, co spowodowane jest specyfiką budowy polimeru taką jak duże ciężary cząsteczkowe, długość łańcuchów, zmiany konformacyjne i przemiany fazowe, sieci fluktuacyjne i inne.

Do właściwości cieplnych należą pojemność cieplna właściwa, przewodność cieplna i rozszerzalność cieplna oraz przewodność temperaturowa.

13.2.1. Pojemność cieplna właściwa

Pojemnością cieplną nazywamy ilość ciepła niezbędnego do ogrzania próbki o 1 K. Wyróżnia się pojemność molową i właściwą. Pojemność właściwa - ciepło powodujące zmianę temperatury o 1K jednostki masy polimera [25]:

, J/(kg⋅K)

Pojemność molowa jest ilością ciepła, które powoduje zmianę temperatury o 1 K jednego mola polimeru (J/(mol⋅K)).

Pojemność oznaczamy przy stałym ciśnieniu (C_p) lub w stałej objętości (C_v) w oparciu o równania:

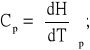
gdzie: H - entalpia;

U - energia wewnętrzna;

V - objętość próbki;

α - współczynnik rozszerzalności termicznej;

K_s - współczynnik sprężenia izotermicznego.

Na ogół pojemność cieplna jest zdolnością polimeru do pochłaniania energii cieplnej wywołującej ruch cząsteczek lub atomów. Wskutek skomplikowanej budowy makrocząsteczek polimerów krystalicznych i amorficznych, ich pojemność składa się z dwóch składowych - spowodowanych przez ruchy segmentów łańcucha głównego i drgania grup lub rozgałęzień bocznych. Ruchy te uzależnione są zarówno od energii oddziaływań międzycząsteczkowych jak i cząsteczkowych wewnętrznych. W obszarach bardzo niskich wartości temperatury (10÷50 K) pojemność cieplna polimerów krystalicznych określa się wzorem (zgodnie z prawem Debye'a):

C_p = T ³.

Zależność ta przedstawiona została graficznie na rys.13.2 - strefa I.

Większa pojemność cieplna polimerów amorficznych w strefie I (strefa niskich temperatur) uwarunkowana jest nieobecnością ułożenia uporządkowanego cząsteczek dalekiego zasięgu i większą w porównaniu z polimerami krystalicznymi objętością swobodną. Natomiast, wzrost C_p dla polimerów amorficznych po przekroceniu T_g spowodowany jest przejściem polimeru w stan wysokoelastyczny (o dużej ruchliwości segmentów).

Wzrost pojemności można zapisać wzorem:

ΔC=ΔC^k+ΔC^v+ΔC^w

gdzie: ΔC^k - przyrost pojemności uwarunkowanej przez zmiany konforma­cyjne (np. trans- w cis-) segmentów makrocząsteczki;

ΔC^v - uwarunkowany przez wzrost objętości swobodnej przy przejściu ze stanu szklistego w stan wysokoelastyczny;

ΔC^w - wyraża zmiany częstotliwości i amplitudy drgań jednostek strukturalnych spowodowanych rozszerzeniem cieplnym przy T_g.

Wartości wymienionych wielkości mają następujące wartości dla niektórych polimerów [25]:

	ΔC^k, J/(mol⋅K)	ΔC^v, J/(mol⋅K)	ΔC^w, J/(mol⋅K)
Poliizobutylen	31-85	40	13
Poli(metakrylan metylu)	13-75	40-61	33
Poli(chlorek winylu)	18-78	52-71	25

Ogólnie można przyjąć, że pojemność cieplna właściwa uzależniona jest od rodzaju polimeru (jego budowy), np. [25]:

	Cp^∗, J/(mol⋅K)		Cp, J/(mol⋅K)
Polietylen	419,6	Polistyren	96,6
Polipropylen: a) ataktyczny	68,3	Poli(metakrylan metylu)	138,6
b) izotaktyczny	90,7	Poli(metakrylan etylu)	218,4

^∗ - oznaczona w temperaturze pokojowej.

Widać, że wzrost objętości podstawników bocznych powoduje zwiększenie C_p.

Charakter zmiany C_p od T w dużym stopniu zależy od struktury nadcząsteczkowej (rys.13.3).

Maksymalne zmiany pojemności ceplnej polimerów występują w zakresie temperatur przejściowych - łagodny wzrost w okresie T_g dla polimerów amorficznych i zmiana skokowa w temperaturze T_m dla krystalicznych. Podalsze ogrzewanie już nie powoduje zauważalnych zmian C_p. Po topnieniu polimeru następuje ustabilizowanie C_p, wartość której według Dulonga-Petita już mało odchyla się od 25 J/(mol⋅K) [25].

Pojemność cieplna właściwa tworzyw sztucznych napełnionych (kompozytów) określa się zależnością:

gdzie: - pojemności cieplne odpowiednio napełniacza i polimeru;

ϕ - ułamek objętościowy napełniacza.

Mierząc pojemność cieplną właściwą w szerokim zakresie temperatur uzyskujemy wiadomości o strukturze nadcząsteczkowej, budowie i postaci badanego polimeru. Stopien krystaliczności polimerów powiązany jest z pojemnością cieplną za pomocą wzoru:

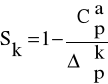
gdzie: - wartość zmiany C_p dla polimerów w stanach amorficznym i krys­ta­licznym w temperaturzę T_g;

a - faza amorficzna;

k - faza krystaliczna.

13.2.2. Przewodność cieplna

Przewodnością cieplną nazywa się proces przewodzenia ciepła od powierzchni o wyższej temperaturze do powierzchni o niższej temperaturze. Jest on uwarunkowany istnieniem gradientu temperatury. Właściwość tę określa się współczynnikiem przewodnictwa cieplnego (λ), który równa się ilości ciepła (Q), przeniesionego w jednostcę czasu przez jednostkową powierzchnię przy gradiencie temperatury 1 K. Zatem przewodność cieplną wyraża się wzorem:

, W/(m⋅K)

Proces przewodzenia ciepła w polimerach rożni się od przewodzenia w metalach, w których główną rolę odgrywa przewodzenie za pomocą elektronów. W polimerze przewodność spowodowana jest drganiami, odbywającymi się w siatce strukturalnej polimeru. Drgania określone są przez fonony - czyli kwanty sprężystych drgań środowiska stałego. Przewodność cieplna polimerów zależy od ich budowy, struktury nadcząsteczkowej i pojemności cieplnej, stanu fizycznego i zmienia się przy zmianie temperatury w różny sposób, zawsze jednak pozostaje uwarunkowana strukturą nadcząsteczkową polimeru (rys.13.4).

W obszarach niskich wartości temperatury (strefa I), spełnia się warunek λ≈1/T³ na skutek niewielkej iłości fononów. W strefie II obserwuje się spadek λ, w wyniku wzrostu ilości fononów spowodowanych ruchliwością jednostek strukturalnych, co zmniejsza wpływ T na λ, który podporządkuje się wtedy zależności λ≈1/T.

Na podstawie teorii przeniesienia fononów sprężystych drgań w siatce, przewodność cieplna oblicza się za pomocą wzoru:

gdzie: C_v - pojemność cieplna właściwa;

- prędkość przeniesienia fononu;

- średnia droga przebiegu dla fononu.

Geometryczne składniki równania (13.19) można zastąpić parametrami molekularnymi, odpowiedającymi strukturze polimeru. Wtedy przewodność będzie określona za pomocą zależności [25]:

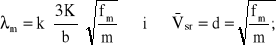
gdzie: k - stała Boltzmanna;

K - stała;

b - długość wiązania chemicznego w jednostce;

f_m - wskaźnik sprężystości wiązania międzycząsteczkowego;

m - masa powtarzalnej jednostki strukturalnej.

Przewodność cieplna polimerów jest zależna od ciężaru cząsteczkowego polimeru. Zależność ta została ustalona przez model Ayermana [25]:

1/λ = 1/λ_∞ + Α/Μ lub 1/λ = 1/λ_∞ + B/Μ^1/2

gdzie: A i B - stałe;

M - ciężar cząsteczkowy polimeru;

λ_∞ - przewodność cieplna polimeru o ciężarze cząsteczkowym nieskończenie wielkim.

Zwiększenie ciężaru cząsteczkowego powoduje wzrost przewodności polimeru wywołanej przez zwiększenie skuteczności odziaływań międzycząsteczkowych, odpowiedzialnych za przeniesienie fononów.

Przewodność maleje ze wzrostem długości rozgałężeń i objętości grup bocznych, zwiększających odległości międzycząsteczkowe.

Orientacja polimerów powoduje anizotropię przewodności: λ w równoległym kierunku do orientacji (λ||) jest większa niż w kierunku prostopadłym (λ⊥). Przewodność energii w równoległym kierunku do orientacji rośnie wskutek wzrostu liczby wiązań międzycząsteczkowych.

Współczynnik anizotropii K_a = λ||/λ⊥ dla amorficznych polimerów dochodzi do 2, a dla krystalicznych może sięgać 50 i więcej.

Przejścia fazowe (krystalizacja, topnienie) wyróżniają się pewnymi zmianami przewodności cieplnej, która wzrasta w procesie krystalizacji i maleje podczas topnienia polimeru krystalicznego.

Na przewodność cieplną wpływ ma też napełniacz, obecność którego na ogół powoduje zwiększenie przewodności [25]:

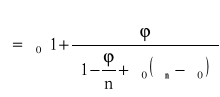
gdzie: λ₀ - współczynnik przewodności cieplnej polimeru;

ϕ - ułamek objętościowy napełniacza;

n - wskaźnik uzależniony od kształtu cząsteczek napełniacza (n=3 w przypadku kulki);

λ_n - współczynnik przewodności napełniacza.

W przypadku oddziaływań chemicznych i fizycznych między napełniaczem a polimerem korzysta się z zależności stosowanych dla elastomerów napełnionych sadzą:

λ=λ₀+Κ_λ⋅m

gdzie: K_λ - współczynnik zależny od typu napełniacza i jego właściwości fizycznych;

m - ułamek masowy napełniacza.

Dla obliczeń wykorzystuje się często parametr określony wzorem:

gdzie: a - współczynnik przewodności temperaturowej;

ρ - gęstość właściwa polimeru.

Oznaczone w temperaturze pokojowej wartości λ i a niektórych polimerów, zestawiono w tabeli 13.2.

Tabela 13.2

Wielkości λ i a dla niektórych polimerów [24,25]

L p.	Polimer	λ, W/(m⋅K)	a⋅10^8, m^2/s
1.	Polietylen: a) małej gęstości	0,380	14,0
2.	b) dużej gęstości (K*)	0,470	12,0÷25,0
3.	Polipropylen: a) ataktyczny (A**)	0,175	−
4.	b) izotaktyczny (K)	0,230	9,0÷13,0
5.	cis-1,4-Poliizopren (A): a) liniowy	0,130	8,9÷9,0
6.	b) usieciowany	0,167	−
7.	c) napełniony sadzą	0,289	−
8.	Polistyren (A)	0,160	9,9
9.	Poli(chlorek winylu) (A)	0,210	12,1
10.	Poli(metakrylan metylu) (A) o ciężarze cząsteczkowym: a) 100⋅10^4	0,190	11,9
11.	b) 2,3⋅10^4	−	10,5
12.	c) 0,66⋅10^4	−	8,9

K* - krystaliczny; A** - amorficzny.

13.2.3. Rozszerzalność cieplna

W stanie równowagi ciało stałe obejmuje objętość odpowiadającą minimalnej energii swobodnej. Ze wzrostem temperatury zwiększa się amplituda drgań atomów i rotacji wokół wiązań. Zjawisko to powoduje wzrost wymiarów próbki w wyniku wzrostu objętości prowadzącego do ustalenia nowych warunków równowagi. Wartościową miarą rozszerzalności jest współczynnik rozszerzalności cieplnej polimeru, który oznacza się w warunkach adiabatycznych (ciśnienie stałe) i wynika z zależności [25]:

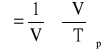
Wzór ten opisuje rozszerzalność objętościową. Liniową rozszerzalność cieplną określa się z wzoru:

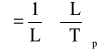
Dla polimerów izotropowych stosowana jest zależnośc:

α = 3β > 0

Współczynnik rozszerzalności cieplnej jest powiązany z pojemnością cieplną zależnością:

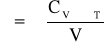
gdzie: γ - stała;

C_v - pojemność cieplna właściwa;

χ_T - miara zwarcia izotermicznego:

χ_T = 1/K_T

K_T - wskaźnik ściskania objętościowego;

V - objętość próbki polimeru.

Wzrost α i β występuje po przekroceniu temperatury zeszklenia (T_g). Wartości β dla niektórych polimerów zestawione są w tabeli 13.3.

Tabela 13.3

Rozszerzalność cieplna polimerów [25]

Polimer	Temperatura, K	β⋅10^4,1/K
				< Tg	> Tg
Polibutadien-cis	171÷161	0,5	2,4
Poliizopren-cis	205÷201	0,7	2,3
Polimetylowinylosiloksan	148÷143	0,9	4,2÷3,5
Kopolimer butadienu i styrenu	222÷217	0,8	2,3

Pomiędzy współczynnikami rozszerzalności cieplnej polimerów w stanie szklistym i wyso­koelastycznym istnieje zależność:

(α_w - α_s)T_g=V_s

gdzie: α_w i α_s - odpowiednio rozszerzalność w stanie wysokoelastycznym i szklistym;

V_s - udział objętości swobodnej, V_s≈0,113.

W obecności napełniacza t.j. sadzy, kredy i innych o udziale objętościowym ϕ=0,3 stosowana jest zależność:

α=α₀-ϕ(α₀-α_n)

gdzie α₀ i α_n - współczynniki rozszerzalności cieplnej polimeru i napełniacza.

Dla polimerów napełnionych zauważamy zmniejszenie się α w stanie szklistym, natomiast w stanie wysokoelastycznym następuje jego zwiększenie wskutek prawdopodobieństwa oddzielenia się polimeru od powierzchni napełniacza.

Polimery orientowane charakteryzują się ujemnym współczynnikiem rozszerzalności cieplnej liniowej w kierunku równoległym do kierunku orientacji. Oznacza to, że wymiary próbki w tym kierunku maleją z podwyższeniem temperatury.

Zatem współczynnik rozszerzalności cieplnej można wykorzystywać zarówno dla obliczeń wymiarów wyrobów oraz dla ustalenia typu struktury, obecności napełniacza i fizycznego stanu polimeru.

13.2.4. Termiczne równanie stanu polimerów

Termiczne równanie stanu polimerów wynika z równania Van der Waalsa i zostało zaproponowane przez Spencera i Gilmore'a w postaci:

(p + π_i) ⋅ (ν_M - ω_M) = RT

gdzie: p - ciśnienie zewnętrzne bezwzględne, określone w odniesieniu do ciśnie­nia próżni absolutnej, MPa;

π_i - ciśnienie wewnętrzne (ciśnienie kohezji) przyjmowane jako niezależne od objętości, MPa;

ν_M - objętość właściwa odniesiona do jednego kilomola polimeru, m³/kmol pod stałym ciśnieniem p i w temperaturze T;

ω_M - wielkość stała interpretowana jako stała objętość makrocząsteczki polimeru w temperaturze zera bezwzględnego, m³/kmol;

R - uniwersalna stała gazowa, R = 8314 J/(kmol⋅K);

T - temperatura polimeru w skali termodynamicznej, K.

Jeżeli uwzględni się związek pomiędzy objętością właściwą odniesioną do jedne­go kilomola ν_M a objętością właściwą odniesioną do jednego kilograma v w pos­taci:

ν_M = M₀ ∙ ν

gdzie M₀ - oznacza ciężar cząsteczkowy wyrażoną w kg na kmol, to korzystując ten wzór i równanie (13.32) otrzymujemy zależność w postaci:

(p + π_i) ∙ (M₀ ∙ ν - ω_M) = RT

a po podzieleniu obu stron tego równania przez M₀:

gdzie: v - objętość właściwa odniesiona do jednego kilograma polimeru, m³/kg;

ω - wielkość stała odniesiona również do jednego kilograma polimeru, m³/kg.

Przyjmując że:

gdzie R' - przedstawia indywidualną stałą gazową wyrażoną w J/(kg⋅K).

Wówczas termiczne równanie stanu polimerów przybierze postać [24]:

Równania (13.35) i (13.37) mają duże znaczenie ze względu na możliwości pomiarowe. Zależność (13.32) można również znaleźć w pracy Smorawińskiego, zaś zależność (13.35) w pracy Łączyńskiego [35].

W tabeli 13.4 zestawiono stałe równania (13.37) dla niektórych polimerów obliczone bądź wyznaczone na podstawie badań eksperymentalnych, w tempe­raturze 175-196 ^oC i na podstawie danych z literatury.

Tabela 13.4

Wartości stałych równania (13.41) niektórych polimerów [24]

Polimer	Ciężar cząsteczkowy monomeru	Stałe
				R′, J/(kg⋅K)	πi, MPa	ω⋅10^-3, m^3/kg
Polistyren	104	80	185,2	0,822
Poli(metakrylan metylu)	100	83	214,6	0,734
Polietylen małej gęstości	28	300	327,3	0,875
Polietylen dużej gęstości	28	300	677,0	1,110
Poliamid-6,10	2,7	3079	1079,0	0,738

180

(13.1)

(13.2)

(13.3)

(13.4)

(13.5)

(13.6)

(13.7)

(13.8)

Rys.13.1. Zależność tgδ (1) i ε (2) od temperatury [22]

(13.9)

(13.10)

(13.11)

(13.12)

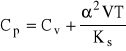
(13.13)

(13.14)

Rys.13.2. Zależność pojemności cieplnej od temperatury dla polimeru krystalicznego (1) i amorficznego (2) [25]

(13.15)

Rys.13.3. Zależność C_p od T dla polimerów:

1 - amorficznych; 2 - częściowo krystalicznych; 3 - wysokokrystalicznych [25]

(13.16)

(13.17)

(13.18)

Rys.13.4. Zależność współczynnika przewod­ności cieplnej od temperatury:

1 - polimer krystaliczny; 2 - amorficzny[25]

(13.19)

(13.20)

(13.21)

(13.22)

(13.23)

m²/s

(13.24)

(13.25)

(13.26)

(13.27)

(13.28)

(13.29)

(13.30)

(13.31)

(13.32)

(13.33)

(13.34)

(13.35)

(13.36)

(13.37)

---