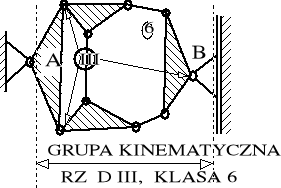
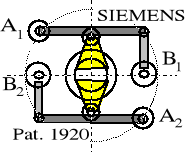
8.3. Sprzęgła odsuwne będące mechanizmami rzędu III.
W rodzajowym zbiorze mechanizmów sprzęgieł odsuwnych (według ilustracji 8.5, zgodnie z tabelą 8.1) istnieje ogromna liczba ich odmian szczegółowych. Podstawą wewnątrzrodzajowego uporządkowania sprzęgieł odsuwnych jest klasyczna teoria mechanizmów [1], która wprowadza (szeroko znane) pojęcie grupy kinematycznej oraz (mniej znane) pojęcie rzędu mechanizmu.
Rząd mechanizmu (w przedmiocie rozważań) określa się liczbą par kinematycznych, za pomocą których grupa kinematyczna musi być skojarzona z nieruchomą podstawą, aby spełnić warunek zerowej jej ruchliwości.
Układ transmisji momentu trakcyjnego w pojeździe musi jednakże mieć co najmniej jedną parę obrotową klasy piątej, stanowiącą modelowe odwzorowanie łożysk osi napędowej, na której, poprzez układ usprężynowania, osadzone jest (ogólnie rozumiane) podwozie pojazdu. W praktyce napędów trakcyjnych oznacza to, iż mechanizmy sprzęgieł odsuwnych są najliczniej reprezentowane jako mechanizmy trzeciego rzędu. Jest ich ogółem nie mniej niż 20 [2]. W tabeli 8.2 zamieszczono jedynie siedem wybranych odmian.
W mechanizmach sprzęgieł odsuwnych rzędu trzeciego dla przekazywania momentu trakcyjnego z wału aktywnego - poprzez najogólniej pojmowaną grupę kinematyczną - na wał bierny, mogą więc być przeznaczone dwie pary kinematyczne czyli praktycznie dwa czopy z osadzonymi na nich łożyskami lub tulejami metalowo - gumowymi. Trzecia para jest łożyskiem osi, której niewspółosiowość powinna być w warunkach trakcyjnych kompensowana najkorzystniej w sposób jednoznaczny. Grupa kinematyczna sprzęgła, będącego mechanizmem klasycznym, powinna więc realizować jednoznacznie względne położenia jej członów. Można też rozważać mechanizmy nieklasyczne realizujące względne położenia członów grupy kinematycznej warunkowo. Jest rzeczą oczywistą, że numer rzędu mechanizmu sprzęgła odsuwnego nie ma ograniczenia od góry.
Zarówno mechanizmy sprzęgieł odsuwnych rzędu trzeciego jak i rzędów wyższych, (zawierające dwa lub więcej czopów na tarczy koła biegowego), w położeniu współosiowości wału biernego względem wału aktywnego, spełniają warunki symetrii przez obrót. Konstrukcja taka w ruchu obrotowym jest dobrze wyrównoważona strukturalnie. Sprzęgła symetryczne przez obrót budzą więc (u konstruktorów) oczekiwania odnośnie możliwości ich dobrego wyrównoważenia także w warunkach niewspółosiowości zmiennej w czasie (wokół montażowego położenia współosiowego).
Jak dotąd, bogata praktyka kolejnictwa zna mechanizmy sprzęgieł odsuwnych rzędu trzeciego. Teoria jednak wskazuje na wyższość mechanizmów rzędu czwartego (bardziej złożonych). Omówiono je kolejno, zarówno w wykonaniu klasycznym jak i nieklasycznym. Mechanizmom sprzęgieł odsuwnych rzędu czwartego poświęcono następny podrozdział (8.4).
Tabela 8.2
L.p |
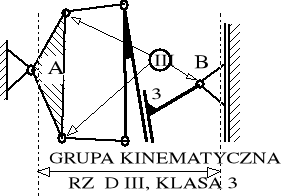
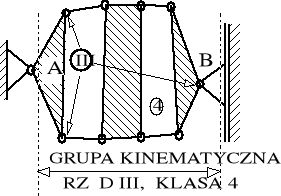
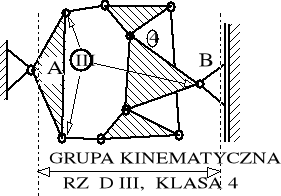
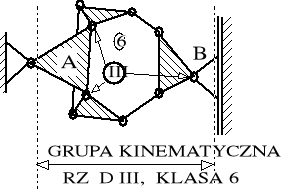
SCHEMAT GRUPY KINEMATYCZNEJ rząd, klasa |
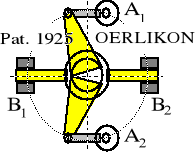
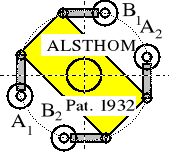
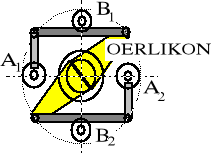
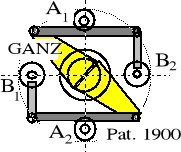
SCHEMAT KONSTRUKCYJNY SPRZĘGŁA |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
Odmiany nieklasyczne sprzęgieł odsuwnych mają człony i więzy sprężyste. Niektóre z tych odmian tylko warunkowo spełniają wymagania trakcyjne.
8.3.1. Badanie kinematyki klasycznych mechanizmów sprzęgieł odsuwnych.
Modele klasycznych mechanizmów sprzęgieł odsuwnych (z członami doskonale sztywnymi, pozbawione luzów) określają podstawową kinematykę trakcyjną układu transmisji momentu w warunkach kompensacji niewspółosiowości wałów. Na tle tak zbadanej kinematyki sztywnych (wyidealizowanych) członów mechanizmów sprzęgieł w praktyce mogą występować dynamiczne zaburzenia ruchu wywołane roboczymi odkształceniami ich członów i więzów sprężystych oraz luzami.
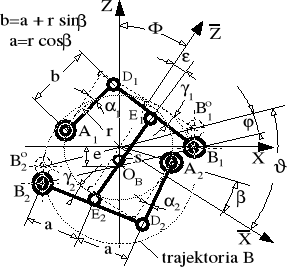
Rysunek 8.6. Odmiana sprzęgła stosowana w lokomotywach FS (Italia) typu
E-444 i E-666 - schemat do badania kinematyki [2].
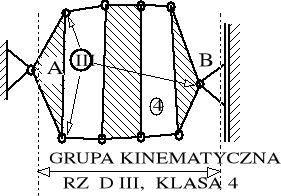
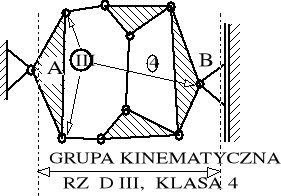
Jako przykład metodyki badawczej kinematyki rozważymy badanie kinematyki sprzęgieł pokazanych w tabeli 8.2 na pozycjach 4 i 7. Sprzęgła te, na pierwszy rzut oka podobne, różnią się między sobą tym, że na poz. 4 pokazano czopy aktywne "A" przyłączone do łączników zaś na poz 7 - przyłączone do dźwigni. Przekonamy się, że pomiędzy tymi odmianami istnieje ogromna różnica jeśli chodzi o zastosowania kolejowe. Jakkolwiek w sprzęgłach tych występują tuleje metalowo - gumowe to, zgodnie z wcześniejszymi uwagami, przeprowadzimy badanie kinematyki struktur wyidealizowanych.
Schemat sprzęgła, pokazanego w tabeli 8.2 na pozycji 4, do badania kinematyki przedstawiono na rysunku 8.6.
Poszczególne człony mechanizmu pokazanego na rysunku 8.6. możemy potraktować wektorowo: ich długości jako moduły wektorów zaś ich położenia jako argumenty. Możemy więc napisać kolejno:
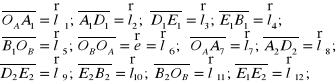
(8.18a)
Zgodnie z rysunkiem 8.6 mamy trzy niezależne równania wektorowe:
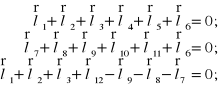
(8.18b)
Powyższe równania wektorowe dają 6 równań rzutów na osie ![]()
ruchomego (wirującego) układu współrzędnych ![]()
.
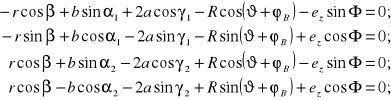
(8.19)
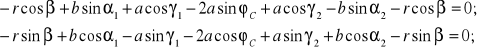
Z równań (8.19) należy wyznaczyć 6 wielkości niewiadomych będących funkcjami zmiennych parametrów pracy sprzęgła: kąta obrotu wału czynnego oraz odsuwności e(t):
![]()
W celu rozwiązania powyższego układu równań zastosujemy rozwinięcia funkcji trygonometrycznych w szereg Taylora względem wielkości małych zachowując dwa wyrazy rozwinięć.
Wprowadźmy następujące oznaczenia dodatkowe:
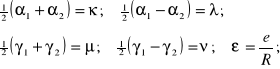
(8.20)
Z powyższego widzimy, że jest rzędu . Jednakże jest znacznie mniejsze od . Możemy więc przyjąć dwa wyrazy rozwinięć w szereg względem i , oraz jeden wyraz rozwinięcia względem i .
Po dodaniu i odjęciu stronami odpowiednio: pierwszego i trzeciego oraz drugiego i czwartego równania (8.19), otrzymujemy nowe cztery równania. Na mocy nowo otrzymanych równań pierwszego i trzeciego wyznaczamy oraz :
![]()
(8.21)
Po podstawieniu (8.21) do odpowiednio uporządkowanych równań powstałych z (8.19), otrzymujemy następujący ich zapis wyznacznikowy:
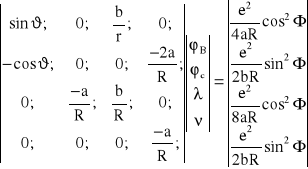
(8.22)
W wyniku rozwiązania (8.22) otrzymujemy rozwiązania
![]()
po odwrotnym wykorzystaniu (8.20), otrzymujemy następujące, jawne zapisy wartości kątów występujących na rysunku 8.6:
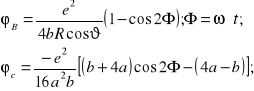
(8.23a)
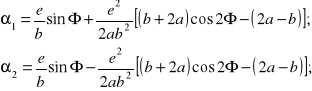
(8.23b)
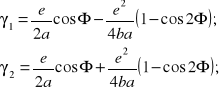
(8.23c)
Pragnąc poprawnie zbudować łącznik - jarzmo łączące punkty E1 i E2 należy zbadać trajektorię punktu charakterystycznego jakim jest środek tego łącznika. Przez otwór w tym łączniku musi bowiem przechodzić oś zestawu kół kolejowych (z odpowiednim luzem promieniowym).
Dla wyznaczenia trajektorii punktu OŁ zapiszemy jego współrzędne w ruchomym układzie odniesienia ![]()
:
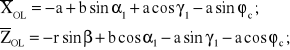
(8.24)
Jawna postać tego zapisu, ze względu na wielkości , i , jest następująca:
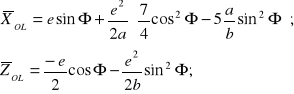
(8.25)
Przechodząc do nie wirującego układu współrzędnych OAXZ, korzystamy z transformacji formalnej:
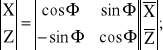
czyli: 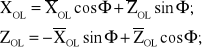
(8.26)
Zatem dla technicznego przypadku e << a; e << b, otrzymujemy:
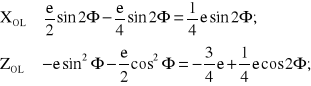
(8.27a)
Równanie okręgu w postaci parametrycznej ma postać następującą:
![]()
(8.27b)
Porównując wielkości w zapisach (8.27a) i (8.27b) otrzymujemy:
![]()
(8.28)
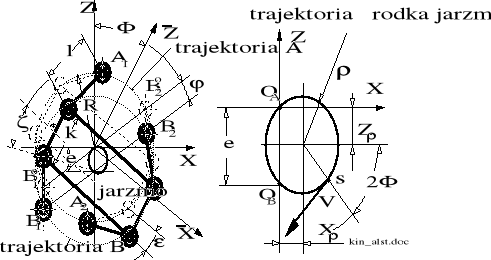
Postać trajektorii punktu charakterystycznego "s" zilustrowano rysunkiem 8.7.
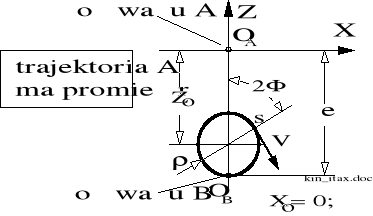
Rysunek 8.7. Postać trajektorii środka łącznika E1-E2 w układzie nie wirującym.
Prędkość "obwodowa" V punktu charakterystycznego "s" wynosi: V=2; przy czym =d/dt; Punkt ten zakreśla więc trajektorię (kołową z określonym przybliżeniem) z podwojoną, w stosunku do prędkości obrotowej wału aktywnego, prędkością kątową wodzącego promienia tej trajektorii, w kierunku zgodnym z kierunkiem ruchu wału aktywnego.
Jeśli wały są współosiowe, czyli "e" = 0, wtedy, zgodnie z (8.28), także V = 0.
Kształt otworu w jarzmie.
Powróćmy ponownie do współrzędnych ruchomych ![]()
i do wzoru (8.25). Jeżeli we wzorze tym odrzucimy wielkości małe wyższego rzędu ograniczając się jedynie do członów opisujących trajektorię kołową to wpływ członów odrzuconych należy uwzględnić zapewniając odpowiedni luz promieniowy w otworze jarzma tak, aby jego wielkość nie wyczerpywała się w dynamicznych warunkach pracy sprzęgła niezależnie od warunków technologicznych wykonania jego jarzma. Kształt otworu w jarzmie, według wzoru (8.25) - obowiązującego dla poz. 4 z tabl. 8.2 - jest określony przez parametry trajektorii punktu "s" względem osi wału aktywnego OA:
![]()
(8.29)
Powyższy zapis jest podstawą analizy kształtu otworu gdy przez (fizyczny) otwór w jarzmie przechodzi (fizyczna) oś wału aktywnego. Odnosi się to do przypadku pokazanego w tabeli 8.2 na pozycji 7.
Kształt tego otworu może być też określony względem osi wału biernego OB, gdy przez otwór w jarzmie przechodzi (fizyczna) oś wału biernego. Taki właśnie przypadek występuje w kolejnictwie według zastosowań opisanych pod rysunkiem 8.6. Taki przypadek pokazano na pozycji 4 w tabeli 8.2 i taki omówimy na początek.
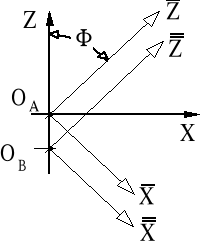
Rysunek 8.8. Szkic pomocniczy wirujących układów współrzędnych związanych z wałem czynnym A i z wałem biernym B do analizy technicznych przypadków kształtu otworu w jarzmie. Kąt odmierza się od osi Z.
Współrzędne położeń osi wału biernego B względem osi wału aktywnego A wyrażone w układzie wirującym ![]()
są następujące:
![]()
(8.30)
I odwrotnie: współrzędne położeń wału czynnego A względem osi wału biernego B wyrażone w układzie wirującym ![]()
, są następujące:
![]()
(8.31)
W mechanizmie sprzęgła, w którym przez otwór w jarzmie przechodzi wał bierny B, (poz.4) półosie ![]()
owalnego otworu w jarzmie muszą (superpozycyjnie) odpowiednio uwzględniać:
fizyczny promień dWB/2 wału biernego przechodzącego przez jarzmo,
promień trajektorii osi A w układzie ![]()
związanym z wałem B,
promień trajektorii punktu "s" środka jarzma według (8.29),
niezbędny promieniowy luz technologiczno - dynamiczny .
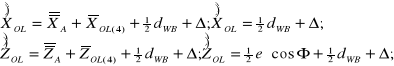
(8.32)
W mechanizmie sprzęgła, w którym przez otwór w jarzmie przechodzi wał aktywny A, obliczając półosie owalnego otworu w jarzmie należy uwzględniać podobne (do powyższych) czynniki:
fizyczny promień dWA/2 wału biernego przechodzącego przez jarzmo,
promień trajektorii osi biernej B zakreślany w wirującym układzie ![]()
związanym z wałem A:
promień trajektorii punktu "s" środka jarzma obowiązujący dla przypadku podanego w tabeli 8.2 na poz. 7, który [2] wynosi:
![]()
(8.33)
niezbędny promieniowy luz technologiczno - dynamiczny .
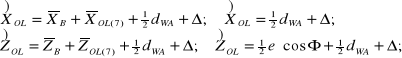
(8.34)
Na mocy (8.33) otrzymujemy następujące wartości półosi owalu:
![]()
(8.35)
Porównanie przypadków: poz. 4 tabl. 8.2 wzór (8.32) oraz poz. 7 tabl. 8.2 wzór (8.35), pokazano na rysunku 8.9.
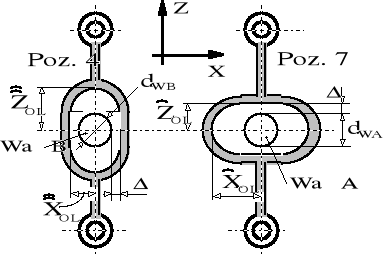
Rysunek 8.9. Kształty łącznika - jarzma dla dwóch omawianych odmian mechanizmu sprzęgła odsuwnego.
Zestawienie wzorów kinematyki najszerzej stosowanych sprzęgieł odsuwnych będących mechanizmami rzędu trzeciego.
Na zakończenie niniejszego podrozdziału zostaną podane zestawienia wzorów kinematyki sprzęgieł Alsthom - poz. 2 w tabl. 8.2, oraz Siemens - poz. 4. i poz 7.
TABELA 8.3. POZ. 1
KINEMATYKA SPRZĘGIEŁ ODSUWNYCH
SPRZĘGŁO LOKOMOTYW EU07 i ET22
W tabeli 8.2 poz. 2; PATENT ALSTHOM Z ROKU 1932
Sprzęgło Alsthom jest szeroko stosowane zwłaszcza w kolejnictwie.
KINEMATYKA SPRZĘGŁA ALSTHOM:
Funkcja położenia sprzęgła: = ;
przy czym: - kątowe położenie wału A - według rysunku;
- kątowe położenie wału B.
![]()
Trajektoria środka jarzma:
![]()
gdzie: V - prędkość środka jarzma na trajektorii.
PROMIENIOWA SZTYWNOŚĆ SPRZĘGŁA (NA ODSUWNOŚĆ):
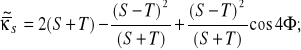
gdzie: ![]()
![]()
- sztywność promieniowa pojedynczej tulejki,
- sztywność skrętna pojedynczej tulejki.
SZTYWNOŚC OBROTOWA (SKRĘTNA - ROBOCZA) SPRZĘGŁA:
![]()
TABELA 8.3. POZ. 2
KINEMATYKA SPRZĘGIEŁ ODSUWNYCH
SPRZĘGŁO LOKOMOTYW E-444 i E-666
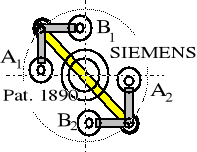
W tabeli 8.2 poz. 4; PATENT SIEMENS Z ROKU 1920
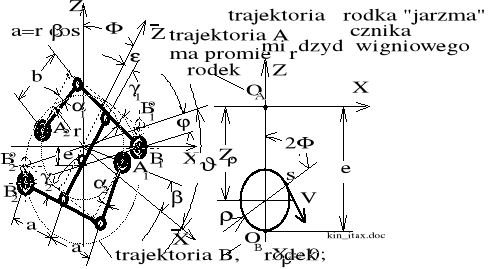
Odmiana sprzęgła stosowana w lokomotywach FS (Italia) typu E-444 i E-666
KINEMATYKA SPRZĘGŁA WEDŁUG PATENTU SIEMENS:
Funkcja położenia sprzęgła: = ;
przy czym: - kątowe położenie wału A - według rysunku;
- kątowe położenie wału B.
![]()
Trajektoria środka łącznika międzydźwigniowego:
![]()
gdzie: V - prędkość środka łącznika międzydźwigniowego na trajektorii.
Kąty obrotu dźwigni i łączników zostały szczegółowo opisane wzorami (8.23).
W przypadku szczególnym (w zastosowanym wykonaniu) =/4; b=a(1+tg);
TABELA 8.3. POZ. 3
KINEMATYKA SPRZĘGIEŁ ODSUWNYCH
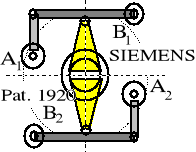
SPRZĘGŁO SIEMENS
W tabeli 8.2 poz. 7. PATENT Z ROKU 1920
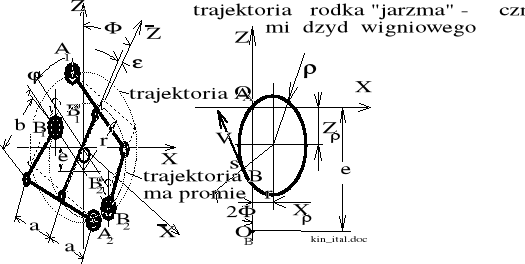
Odmiana sprzęgła nie stosowana w kolejnictwie.
KINEMATYKA SPRZĘGŁA
Funkcja położenia sprzęgła: = ;
przy czym: - kątowe położenie wału A - według rysunku;
- kątowe położenie wału B.
Funkcja położenia sprzęgła dla przypadku a = b:
![]()
Trajektoria środka łącznika międzydźwigniowego:
![]()
gdzie: V - prędkość środka łącznika międzydźwigniowego na trajektorii.
Literatura źródłowa do podrozdziału 8.3.
[1] Artobolewskij I. I.: Mechanizmy v sovremennoj technikie. Moskwa "Nauka" 1970.
[2] Madej J.: Mechanika napędu pojazdów szynowych... PWN Warszawa 1983.
[3] Madej J.: Projektowanie mechanizmów napędowych pojazdów szynowych WKiŁ Warszawa, 1988.
183
Wyszukiwarka
Podobne podstrony:
ROZDZ 8U, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8K, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 10B, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8E, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 5A, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8G, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8O, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8A, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 10A, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 7A, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8P, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ROZDZ 8T, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
COVER, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
TBL891, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
TBL871, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
TBL872, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, MTMT
ACOVER, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
A-rys1-10, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
A-Rzdz3, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Uklady napedowe, TeoRuch
więcej podobnych podstron