ZADANIA
ANALIZA MATEMATYCZNA
Wyznaczyć granicę funkcji:
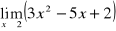
;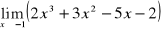
;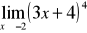
;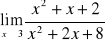
;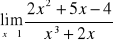
;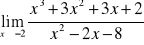
;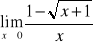
;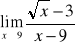
;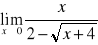
;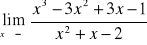
;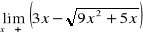
;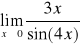
;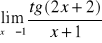
;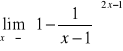
;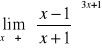
;
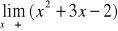
;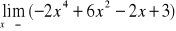
;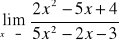
;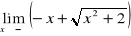
.
Dla niżej podanych funkcji wyznacz dziedzinę, granicę lewostronną i prawostronną w punktach, w których nie są określone:
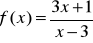
,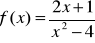
.
Obliczyć jednostronne granice funkcji. Czy istnieje granica funkcji w punkcie
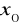
?
a) ![]()
w punkcie ![]()
,
b) ![]()
w punkcie ![]()
,
c) 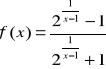
w punkcie ![]()
.
Wykaż, że nie istnieje granica
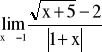
.Wyznacz równania wszystkich asymptot wykresu funkcji o wzorze
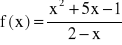
.
Zbadaj, czy funkcja jest ciągła w punkcie
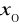
. W przypadku nieciągłości określić jej rodzaj.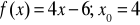
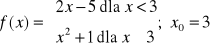
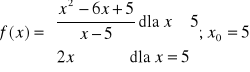
.
Znajdź skok funkcji
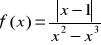
w punkcie nieciągłości.Zbadaj, czy funkcja jest ciągła w całej swojej dziedzinie
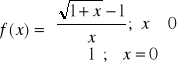
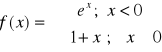
.Dana jest funkcja
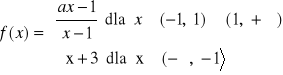
.
Wyznacz a tak, aby funkcja była ciągła w punkcie x0 = -1. Narysuj wykres funkcji dla wyznaczonego a.
Oblicz na podstawie definicji pochodną funkcji
f(x) =
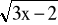
w punkcie x0 = 1.f(x) =
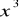
w punkcie x0 .
Oblicz pochodną funkcji , gdy:
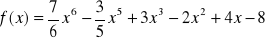
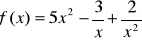
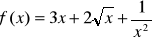
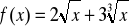
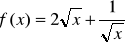
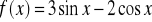
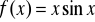
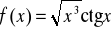
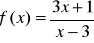
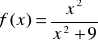
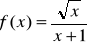
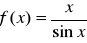
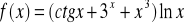
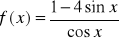
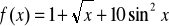
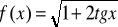
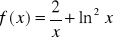
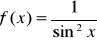
.
Napisać równania stycznych do krzywej o równaniu
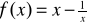
w punktach przecięcia się jej z osią odciętych.Dane są dwa punkty A(1, 2), B(3, 10) należące do wykresu funkcji
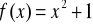
. Napisać równanie siecznej przechodzącej przez te punkty i równanie stycznej równoległej do tej siecznej.Wyznacz przedziały monotoniczności funkcji:
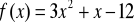
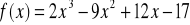
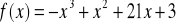
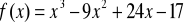
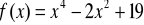
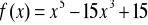
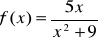
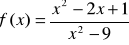
Wyznacz ekstrema funkcji:
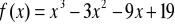
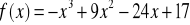
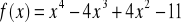
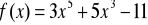
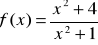
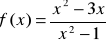
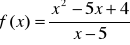
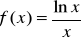
.
Wyznacz ekstrema globalne funkcji
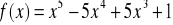
w przedziale <-1, 2>,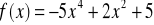
w przedziale <-2, 2>,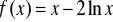
w przedziale <1, e>,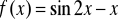
w przedziale ,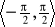
.
Znaleźć pochodną rzędu drugiego funkcji
Wyznaczyć punkty przegięcia oraz przedziały wypukłości i wklęsłości funkcji
Wyznacz przedziały monotoniczności wielomianu
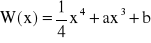
, jeśli wiadomo, że reszta z dzielenia wielomianu W(x) przez dwumian (x - 2) wynosi -2, zaś współczynnik kierunkowy stycznej do jego wykresu w punkcie odciętej 1 wynosi -1.Dana jest funkcja f(x) =
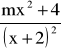
, x ∈ R - {-2}.
a) Dla jakich m asymptotą poziomą wykresu funkcji jest prosta o równaniu y = 3?
b) Dla m = 1 wyznacz ekstrema funkcji f.
Na krzywej o równaniu xy = 4 obrano punkty A(1, 4) oraz B(2, 2). Wyznacz na krzywej taki punkt C o ujemnych współrzędnych, aby pole ΔABC było najmniejsze.
Liczbę dodatnią przedstawić w postaci sumy dwóch składników dodatnich tak, aby iloczyn ich był możliwie największy.
Długości ramion i mniejsza podstawa trapezu mają po 10 cm. Wyznaczyć jego większą podstawę tak, aby pole trapezu było największe.
Skrzynka z pokrywą w kształcie prostopadłościanu ma mieć pojemność 576 cm3. Krawędzie podstawy mają być w stosunku 1:2. Jakie powinny być wymiary wszystkich krawędzi, aby na skrzynkę zużyć jak najmniej materiału.
Działkę prostokątną o powierzchni 1250 m2 i przyległą jednym z boków do kanału należy ogrodzić płotem. Jakie powinny być wymiary działki, aby długość płotu była najmniejsza.
Okno o obwodzie 2p ma kształt prostokąta zakończonego półkolem. Jakie powinny być wymiary części prostokątnej okna, aby ilość światła przenikającego przez nie była jak największa.
Cena zbytu pewnego wyrobu jest ustalona i równa p zł/jedn. Koszt całkowity K(x) (zł) produkcji jest zależny od wielkości (x jedn.) produkcji według wzoru K(x)=0,1x2+10x+40. Przy jakiej wielkości produkcji zysk przeciętny na jednostce wyrobu jest największy.
Zapas z ton pewnego towaru w magazynie zmienia się w ciągu miesiąca (30 dni) i po upływie t dni (licząc od początku miesiąca) wyraża się wzorem z(t)=0,01t3+0,15t2-18t+300. W którym dniu zapas ten jest najmniejszy. Jaki jest średni zapas w ciągu miesiąca.
W pewnym fikcyjnym przedsiębiorstwie funkcja kosztów przeciętnych jest następująca kp(x)=0,1x2-3x+40+x-1. Przy jakiej wielkości produkcji koszt krańcowy będzie najmniejszy.
Zbadaj przebieg zmienności funkcji
Funkcja kosztu całkowitego pewnego przedsiębiorstwa jest określona wzorem
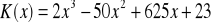
, gdzie x oznacza wielkość produkcji (w jednostkach miary). Zbadać tę funkcję i narysować jej wykres.
4
Wyszukiwarka
Podobne podstrony:
WYKLAD ANALIZA MATEMATYCZNA
Analiza matematyczna, lista analiza 2008 6 szeregi
Analiza Matematyczna 1 Gewert Skoczylas zadania
Analiza Matematyczna Twierdzenia
Analiza matematyczna 1
Praca domowa 2a Analiza Matematyczna
Zadania z Analizy Matematycznej, Matematyka
zestaw9, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
Analiza matematycza opracowanie pytań
Kolos 3 Analiza matematyczna
analiza matematyczna 7
Analiza matematyczna 2 Przyklady i zadania
cw 13 Analiza Matematyczna (calki) id
Analiza matematyczna 1, tab
,analiza matematyczna 2, elemen Nieznany (2)
zestaw10, Matematyka stosowana, Analiza, Analiza matematyczna dla leniwych
a2k, WTD, analiza matematyczna
CALY E -TRAPEZ, PWR, Analiza Matematczna
więcej podobnych podstron