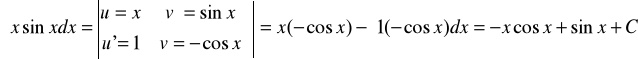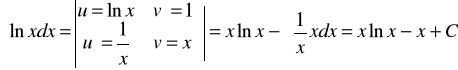∫ CAŁKI ∫
CZĘŚĆ I Rodzaje, podstawowe wzory i definicje, sposoby rozwiązywania
CZĘŚĆ II Obliczanie przykładowych zadań
Całki
Funkcja pierwotna i całka nieoznaczona
Funkcja pierwotna.
Funkcję F(x) nazywamy funkcją pierwotną funkcji f(x) na zbiorze X, jeżeli dla każdego x∈X spełniony jest warunek: F'(x)=f(x).
Twierdzenie o funkcjach pierwotnych
Jeżeli F(x) jest funkcją pierwotną funkcji f(x) na przedziale P to:
funkcja φ(x)=F(x)+C, gdzie C oznacza dowolną stałą, jest także funkcją pierwotną na przedziale P,
każdą funkcję pierwotną φ(x) funkcji f(x) na przedziale P można przedstawić w postaci sumy F(x)+C0, gdzie C0 jest stosownie do φ(x) i F(x) dobrana stałą.
Całka nieoznaczona.
Zbiór wszystkich funkcji pierwotnych funkcji f(x) na przedziale X nazywamy całką nieoznaczoną funkcji f(x) na tym przedziale i oznaczamy symbolem: ![]()
Z twierdzenia o funkcjach pierwotnych wynika, że ![]()
, gdzie F(x) jest jakąkolwiek funkcją pierwotną funkcji f(x) na rozważanym przedziale, C natomiast jest stałą dowolną, zwaną stałą całkowania.
Tablica wzorów podstawowych:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Całkowanie przez części
Tw. Jeżeli funkcje u(x) i v(x) mają na pewnym przedziale ciągłe pochodne u'(x) i v'(x), to ![]()
na tym przedziale.
Całkowanie przez podstawianie
Tw. Jeżeli funkcja t=h(x) ma ciągłą pochodną h'(x) na przedziale P i przekształca go na przedział T, na którym określona jest ciągła funkcja g(t), to ![]()
, przy czym w całce nieoznaczonej po prawej str. znaku równości obowiązuje podstawienie h(x) w miejsce t.
II. Całka oznaczona
Tw. Newtona-Leibniza.
Jeżeli funkcja f(x) jest ciągła na przedziale <a,b>, F(x) zaś jest jakąkolwiek jej funkcją pierwotną na tym przedziale, to: 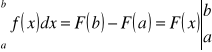
III. Zastosowanie geometryczne całek
Pole figury płaskiej
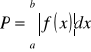
Objętość bryły obrotowej
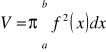
Pole powierzchni bocznej bryły obrotowej
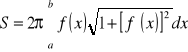
Długość łuku gładkiego, będącego wykresem funkcji y=f(x) na przedziale <a,b>
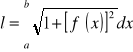
Całki - zadania przykładowe
Całkowanie przez części
∫ u(x) ′(x) dx = u(x)v(x) - ∫ v(x)u′(x) dx
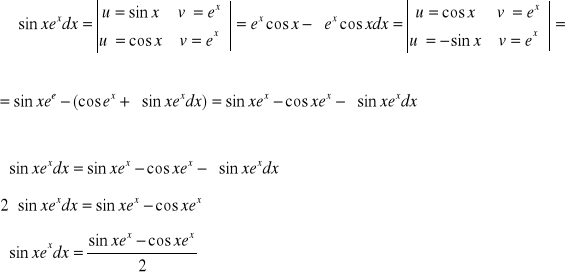
4.)
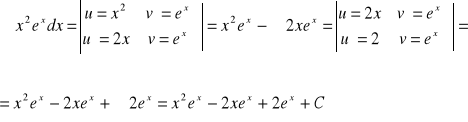
Całkowanie przez podstawianie
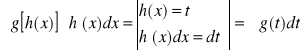
1.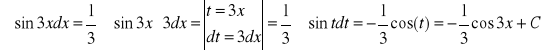
2.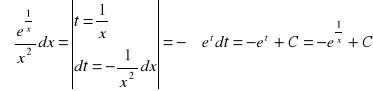
3.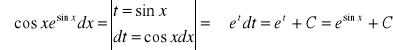
III. Całka oznaczona
![]()
1.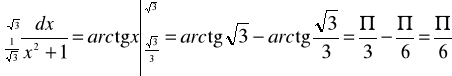
2.![]()
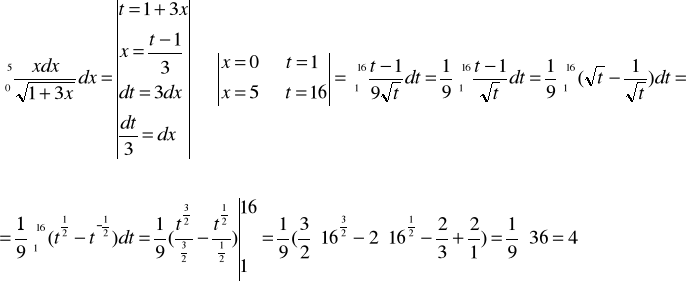
3.Oblicz pole figury F
a)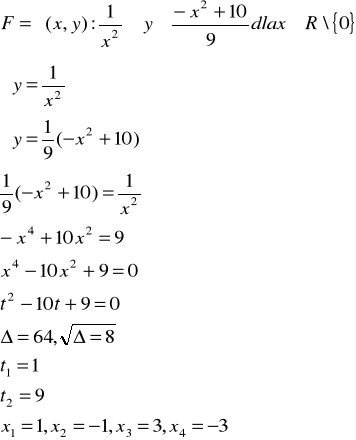
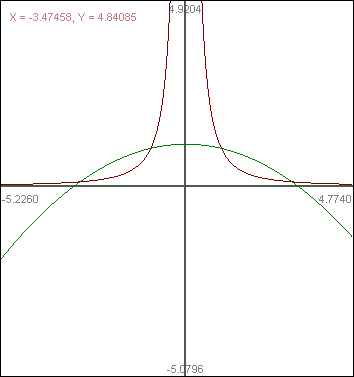
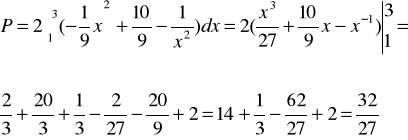
4) Oblicz objętość bryły powstałej w wyniku obrotu krzywej
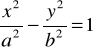
![]()
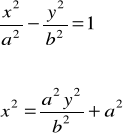
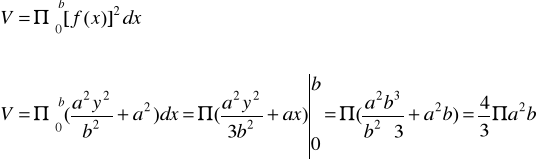
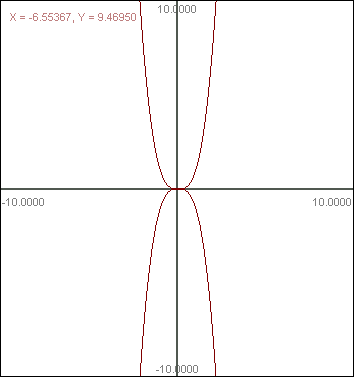
5) Oblicz pole boczne bryły powstałej z obrotu wokół osi x krzywej ![]()
w przedziale 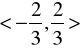
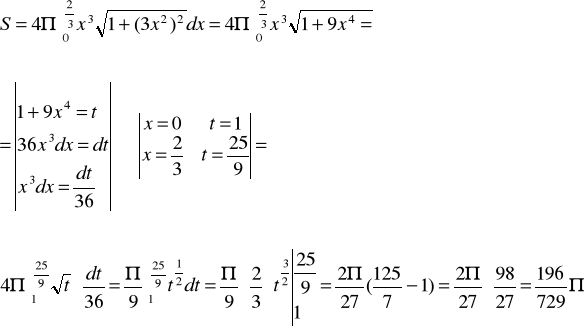
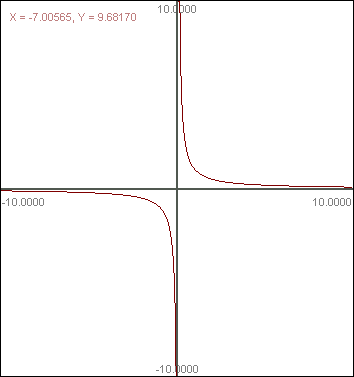
6.Oblicz pole figury ograniczonej wykresem w przedziale
![]()
![]()
![]()
![]()
![]()
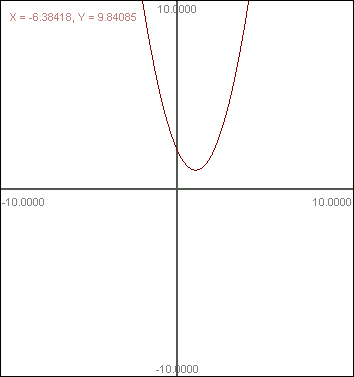
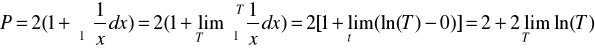
Oblicz pole pod krzywą
![]()
![]()
P= 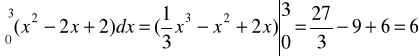
Zadania c.d.- różne
1.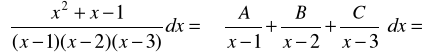
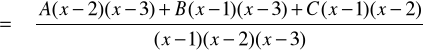
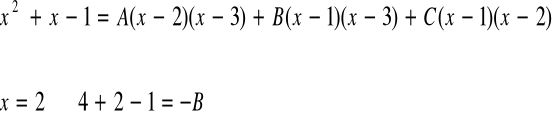
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
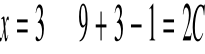
![]()
![]()
![]()
![]()
![]()
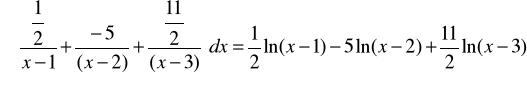
2.
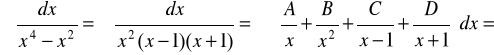
![]()
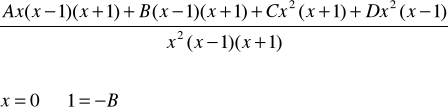
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
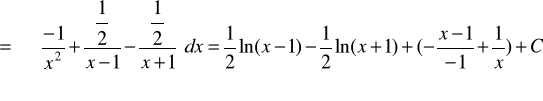
3.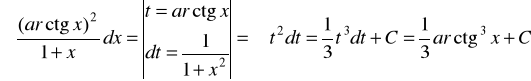
4.
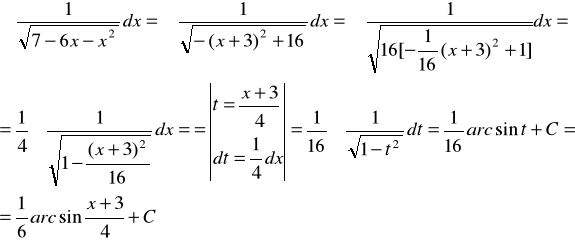
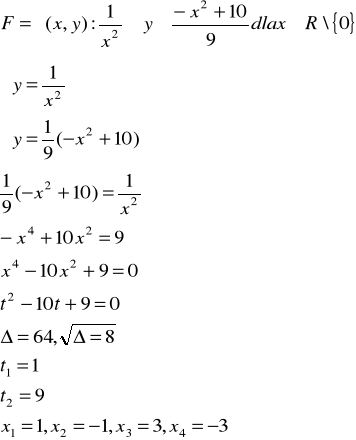
Wyszukiwarka
Podobne podstrony:
Rozniczka elast tempo, STUDIA MATERIAŁY, MATEMATYKA
metodaJG, STUDIA MATERIAŁY, MATEMATYKA
Rozwinięcie Taylora1, STUDIA MATERIAŁY, MATEMATYKA
ZADANIA-matfin, STUDIA MATERIAŁY, MATEMATYKA
Przebiego1, STUDIA MATERIAŁY, MATEMATYKA
Krzywe Tornquista-m, STUDIA MATERIAŁY, MATEMATYKA
Granica wn, STUDIA MATERIAŁY, MATEMATYKA
Zadfindodatkowe2, STUDIA MATERIAŁY, MATEMATYKA
Granica n, STUDIA MATERIAŁY, MATEMATYKA
matfinan-wz, STUDIA MATERIAŁY, MATEMATYKA
Granice wł, STUDIA MATERIAŁY, MATEMATYKA
Granica, STUDIA MATERIAŁY, MATEMATYKA
ukladyrow, STUDIA MATERIAŁY, MATEMATYKA
Liczba Pi, STUDIA MATERIAŁY, MATEMATYKA
Zadfindodatkowe1, STUDIA MATERIAŁY, MATEMATYKA
więcej podobnych podstron