Zad1.
Niech ![]()
będzie przestrzenią probabilistyczną. Wskazać zdania prawdziwe: dla dowolnych zbiorów A, B ![]()
zachodzi
P(A

B)=P(A)*P(B)P(A

B)
P(B)P(A

B)
P(A) + P(B)P(A \ B) =P(A) - P(B)
Zad 2.
Doświadczenie polega na rzucie kostką do gry- rzucamy nią tak długo, aż wypadnie szóstka. Niech ![]()
oznacza zdarzenie, że za i-tym razem po raz pierwszy wypadła szóstka. Ocenić prawdziwość poniższych zdań:
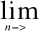
P(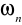
) = 0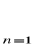
P(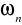
) = 1P(
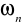
) =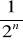
, dla każdego n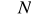
Zdarzenia
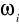
są jednakowo prawdopodobne
Zad 3.
Ocenić prawdziwość poniższych zdań:
Każda zmienna ma skończoną wartość oczekiwaną.
Istnieją zmienne losowe, dla których nie istnieje skończona wartość oczekiwana
Istnieje zmienna losowa, dla której wszystkie momenty centralne są równe zeru
Wariancja sumy zmiennych losowych jest równa sumie wariancji tych zmiennych pod warunkiem, że wariancje istnieją i są skończone.
Zad 4.
W schemacie Bernoullego liczba doświadczeń wynosi 10, a prawdopodobieństwo sukcesu wynosi p=0,7. Które z poniższych zdarzeń jest najbardziej prawdopodobne?
Uzyskanie 2 sukcesów
Uzyskanie 3 sukcesów
Uzyskanie mniej niż 2 sukcesów
Uzyskanie więcej niż 5 sukcesów
Zad 5.
Które z poniższych wykresów przedstawiają wykres dystrybuanty?
Zad 6.
Które z wykresów w zad 5. Przedstawiają wykres dystrybuanty rozkładu ciągłego?
Zad 7.
Które z wykresów w zad 5. Przedstawiają wykres dystrybuanty rozkładu dyskretnego?
W zad 8. Również wykres i pytanie o dystrybuantę, niestety odpowiedzi nie uchwyciło.
Zad 9,
Zmienna losowa X ma rozkład Poissona z parametrem ![]()
. Wskazać zdania prawdziwe:
P ( X = 0 ) = 0.5
PX=1 ////cholernie nieczytelne
P ( X = 1 ) = 0.5
P ( |X - 1|

2 ) = 0.25P(X

t)-> 1 gdy t->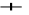
Zad 10.
Zdarzenia losowe ![]()
są niezależne i każde z nich ma rozkład N(0,1). Które z poniższych zdań są prawdziwe:
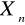

N(0,1)E(
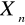
) = 0E(
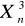
) = 1E(
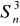
) = 1E(n
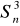
) = n - 1Cov(
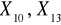
) = 0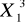
+ … +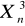
ma rozkład ?? kwadrat o n stopniach swobody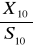
ma rozkład Studenta o 9 stopniach swobody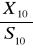
ma rozkład Studenta o 3 stopniach swobodyE(
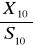
) = 0
Zad 11.
Zmienne losowe ![]()
są niezależne i mają ten sam rozkład, przy czym E![]()
, ![]()
, istnieją dla każdego i ![]()
N oraz E![]()
= m, ![]()
= ![]()
> 0. Które z poniższych zdań są prawdziwe:
P(|
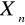
- m| < 3) -> 0, gdy n->
P(|
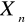
- m| < 1) -> 1, gdy n->
P(|
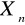
- m|
1)
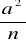
P(
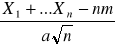

3) -> 0 gdy n->
P(
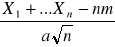
> 0) ->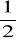
gdy n->
Zad 12.
Poziom istotności testu jest to prawdopodobieństwo:
Popełnienia błędu I rodzaju
Odrzucenia hipotezy fałszywej
Przyjęcia hipotezy prawdziwej
Odrzucenia hipotezy prawdziwej
Zad 13.
Czterech koszykarzy amatorów ćwiczyło rzuty za 3 punkty. Pierwszy z nich trafił za drugim razem, drugi za trzecim, trzeci- za czwartym, a czwarty za pierwszym. Zakładając dla wszystkich graczy jednakową celność, metodą największej wiarygodności wyznaczono estymator p nieznanej wartości p. Oceń prawdziwość poniższych zdań:
p < 0,5
p < 0,4
p = 0,4
p

0,5
Zad 14.
Z pewnej populacji w której iloraz inteligencji posiada rozkład N(m,10), wybrano losowo 10000 osób, zbadano ich iloraz inteligencji otrzymując średnią 123,5, a następnie na poziomie istotności ![]()
= 0,1 przetestowano tezę ![]()
: m = 124, przy alternatywie ![]()
: m < 124. Oceń prawdziwość poniższych zdań:
Wynik testu sugerował odrzucenie
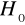
na korzyść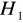
Wynik testu świadczył o tym, iż nie ma podstaw do odrzucenia hipotezy
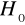
Nie byłoby podstaw do odrzucenia
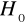
, gdyby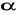
było równe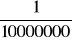
Wyszukiwarka
Podobne podstrony:
zmienne losowe dyskretne id 591 Nieznany
590 591
591
591
591
591
591
591
591
591
591
Elektroniczny detektor niesczelnosci 1 687 001 591
591
591
Fizjoterapia 551 591
591
zmienne losowe dyskretne id 591 Nieznany
591 Pickart Joan Elliot Miłość z lat szkolnych 2
więcej podobnych podstron