4.6 Odwzorowanie Gaussa-Krügera (klasyczne)

Definicja:

Odwzorowanie Gaussa-Krügera jest to wiernokątne, poprzeczne, walcowe odwzorowanie elipsoidy obrotowej na płaszczyznę, realizowane w wąskich pasach południkowych.

Spełnia następujące warunki:

• południk środkowy (osiowy) pasa odwzorowuje się na odcinek linii prostej,

• skala długości na południku środkowym jest równa jedności: m₀=1, a₀=b₀=1

Kształt siatki kartograficznej:

• południk środkowy odwzorowuje się wiernie na odcinek linii prostej, pozostałe południki na krzywe symetryczne względem południka środkowego (wklęsłością do obrazu południka środkowego)

• równik odwzorowuje się na odcinek linii prostej, prostopadłej do południka środkowego, równoleżniki - na linie krzywe symetryczne względem obrazu równika (wypukłością do obrazu równika)

Obraz całej elipsoidy ma postać porozcinanych pasów południkowych. Ograniczenie obszaru

do wąskich pasów południkowych ma na celu minimalizację zniekształceń odwzorowawczych.

Wzory odwzorowania Gaussa-Krügera (B,L → X,Y)

Element łuku:
- na elipsoidzie,

- na płaszczyźnie

Uwaga: łuki odpowiadające równym przyrostom argumentów B i L nie są sobie równe.

Wprowadzimy szerokość izometryczną q:

,

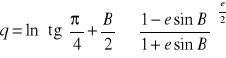
ażeby:

Szerokość izometryczna sprawia, że otrzymujemy równe wartości łuków południka i równoleżnika dla równych przyrostów dq i dL.

Skala odwzorowania:

Wykorzystując fakt, że dq i dL są różniczkami niezależnych zmiennych B i L można zapisać skalę jako funkcję zmiennych zespolonych:

Warunek równokątności odwzorowania oznacza, że skale są niezależna od azymutu elementów liniowych dS i ds (równe w każdym punkcie)

warunkiem odwzorowania jest x=S - długość łuku południka osiowego tzn. odcięte muszą być równe długości łuku południka.

Po rozwinięciu w szereg Taylora funkcji f(q+il) względem il , po oddzieleniu części rzeczywistej od urojonej

otrzymamy:

gdzie:

Zbieżnością południków w odwzorowaniu nazywamy kąt zawarty między styczną do obrazu południka w danym punkcie a linią prostą przechodzącą przez ten punkt równolegle do osi x.

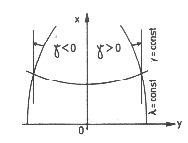
Zbieżność południków γ mierzona jest od stycznej do obrazu południka.

We wszystkich punktach odwzorowania Gaussa - Krügera, leżących na północ od obrazu równika i na wschód od obrazu południka środkowego danego pasa, zbieżność południków jest, dodatnia.

Kąt zbieżności południków wyrażony w funkcji odległości od południka środkowego (z dokładnością 0.001″ dla l = ±3.5°) wynosi:

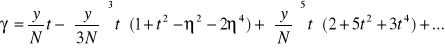
Elementarne skale długości i pól

Odwzorowanie Gaussa-Krügera jest odwzorowaniem równokątnym, zatem elementarna skala długości w danym punkcie jest jednakowa we wszystkich kierunkach. Najłatwiej można ją obliczyć w funkcji odległości od południka środkowego:

lub

gdzie R - średni promień krzywizny.

Elementarną skalę pól obliczymy jako kwadrat skali m:

Odwzorowanie Gaussa-Krügera w położeniu siecznym

Odwzorowanie Gaussa-Krügera często realizowane jest w położeniu siecznym, co oznacza, że powierzchnia walca przecina powierzchnię elipsoidy wzdłuż linii przebiegających w przybliżeniu południkowo. Celem takiego postępowania jest zminimalizowanie zniekształceń:

• wzdłuż linii przecięcia obu powierzchni zniekształcenia będą zerowe,

• na obszarze między liniami przecięcia zniekształcenia będą mniejsze lecz ujemne (skurczenie) o maksymalnej wartości bezwzględnej na południku środkowym,

• na pozostałym obszarze zniekształcenia będą mniejsze ale dodatnie, tym większe im większa będzie odległość od linii przecięcia.

Odwzorowanie sieczne charakteryzuje skala długości m₀ na południku środkowym. Współrzędne
w odwzorowaniu siecznym oblicza się z wzoru: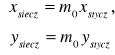

zaś elementarna skala długości w dowolnym punkcie będzie równa:

Współrzędne cechowane

Z wzorów na współrzędne x,y w odwzorowaniu Gaussa-Krügera otrzymujemy wartości w układzie, którego początek zaczepiony jest w punkcie przecięcia południka środkowego pasa odwzorowawczego z równikiem czyli w układzie pojedynczego pasa. Wygodnie jest przesunąć początek tego układu tak, aby uzyskać jednolite i dodatnie współrzędne o jednakowej liczbie cyfr. Wymagania te spełniają współrzędne cechowane. Między współrzędnymi cechowanymi X,Y a współrzędnymi x,y w odwzorowaniu Gaussa-Krügera (dla 3- i 6-stopniowych pasów) zachodzą następujące związki:

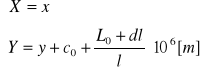
gdzie: c₀ = 500 000 m,

L₀ = długość geodezyjna południka środkowego w [°],

l - szerokość pasa odwzorowawczego w [°] (najczęściej 3° lub 6°),

dl =3° dla pasa 6-stopniowego i dl =0° dla pasa trzy-stopniowego

Zastosowanie odwzorowania Gaussa-Krügera w Polsce

1. W 1920 r. wprowadzono odwzorowanie Gaussa-Krugera do obliczeń wyników triangulacji państwowej (układ współrzędnych „Borowa Góra”):

• elipsoida Bessela,

• pięć 2-stopniowych pasów odwzorowawczych dla południków środkowych: 17°, 19°, 21°, 23°, 25°,

• skala m₀ = 1, X = x - 5 280 000 m, Y = y + 90 000 m

2. W 1947 r. wprowadzono skurczone odwzorowanie G-K dla map 1:10000 i większych:

• elipsoida Bessela,

• cztery 3-stopniowe pasy odwzorowawcze dla południków środkowych: 15°, 18°, 21°, 24°,

• skala m₀ = 0.999935, X = x, Y = y +(5 500 000, 6 500 000, 7 500 000, 8 500 000) m dla kolejnych pasów odwzorowawczych,

Od 1949 r. zmieniono skalę na południkach środkowych na m₀=1.

3. W 1952 r. wprowadzono nową wersję odwzorowania G-K (układ „1942”):

• elipsoida Krasowskiego,

• trzy 6-stopniowe pasy odwzorowawcze dla południków środkowych: 15°, 21°, 27°,

• skala m₀ = 1, X = x, Y = y +(3 500 000, 4 500 000, 5 500 000, 8 500 000) m dla kolejnych pasów odwzorowawczych.

4. W 1965 r. we wprowadzanym układem współrzędnych „1965”, w jednej jego strefie (V-strefa katowicka) zastosowano odwzorowanie G-K:

• elipsoida Krasowskiego,

• jeden pas odwzorowawczy L₀ = 18°57′30 (szerokość pasa ok.1.5°),

• skala m₀ = 0.999983, X = x - 4 700 000 m, Y = y + 237 000 m.

5. W 1992 r. wprowadzono nowy układ współrzędnych „1992”, w którym zastosowano kolejną wersję odwzorowania G-K:

• elipsoida WGS-84,

• jeden 12-stopniowy pas odwzorowawczy dla całej Polski (L₀ = 19°),

• skala m₀ = 0.9993, X = x - 5 300 000 m, Y = y + 500 000 m.

Odwzorowanie to jest obowiązującym (Rozp.R.M. z dnia 8.08.2000) odwzorowaniem dla map w skalach 1:10000 i mniejszych,

6. W 2000 r. wraz z utworzeniem nowego układu współrzędnych „2000”, wprowadzono nową wersję odwzorowania G-K:

• elipsoida WGS-84,

• cztery 3-stopniowe pasy odwzorowawcze (15°, 18°, 21°, 24°),

• skala m₀ = 0.999923, X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m dla kolejnych pasów odwzorowawczych.

Odwzorowanie to jest obowiązującym odwzorowaniem dla mapy zasadniczej (Rozp.R.M. z dnia 8.08.2000),

Kartografia matematyczna. Odwzorowanie Gaussa-Krügera - skrót

3

---