4.2 Odwzorowania azymutalne

Definicja

Odwzorowaniem azymutalnym normalnym nazywamy odwzorowanie powierzchni kuli na płaszczyznę, w którym spełnione są dwa następujące warunki:

• obrazy południków tworzą pęk prostych przecinających się pod takimi samymi kątami jak południki na kuli,

• 
  
  obrazy wszystkich równoleżników są kołami współśrodkowymi, których środek leży w wierzchołku powyższego pęku

gdzie
- funkcja kąta p,

W płaszczyźnie stycznej przyjmujemy układ współrzędnych o środku w biegunie i o osi X stycznej do południka zerowego. Kat γ jest równy długości λ.

Dla tak przyjętych układów równania obu powierzchni będą miały postać:

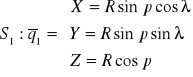
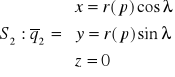
(4.2.1)

Znajdujemy następnie skalę odwzorowania:

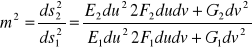
(4.2.2)

oraz współczynniki I formy kwadratowej dla kuli (S₁) oraz dla płaszczyzny (S₂):

,

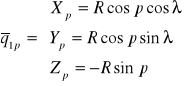
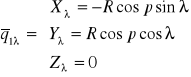
- I forma kwadratowa dla kuli

W dalszej kolejności wyznaczymy
dla płaszczyzny:

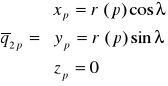
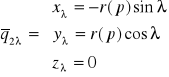
czyli

Zatem wzór ogólny na skalę w odwzorowaniu azymutalnym będzie miał postać:

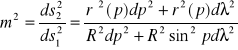
Następnie wyznaczymy skale główne odwzorowania. Kierunki główne pokrywają się tu z kierunkami południków i równoleżników (linii parametrycznych)

Skala w kierunku południków:

,

→

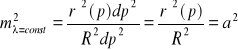
Skala w kierunku równoleżników:
,

→

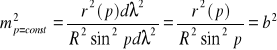
Mając wzory na skale w kierunkach głównych możemy poszukiwać odwzorowań o z góry zadanych właściwościach.

4.2.1 Odwzorowania azymutalne

Rzut ortograficzny (Apoloniusz z Pergii 250-190 r. p.n.e. lub Hipparch ok. 130 r. p.n.e.)

Jeśli rzutowanie powierzchni kuli na płaszczyznę zrealizujemy wzdłuż prostych prostopadłych do płaszczyzny rzutów, to otrzymamy rzut ortograficzny.

Zgodnie z rysunkiem funkcja r(p) będzie równa:

A więc funkcje odwzorowawcze tego odwzorowania będą miały postać:

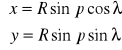
Skale w kierunkach głównych oraz zniekształcenia w tym odwzorowaniu wyniosą:

- skrócenie w kierunku południków,

- zachowanie długości w kierunku równoleżników

Zniekształcenie kąta będzie równe:

czyli
- kąty ulegają powiększeniu.

Skala pola będzie równa:

- pola powierzchni zmniejszeniu

Obraz półkuli mieści się w kole o promieniu R, wszystkie równoleżniki zachowują swoją długość.

Rzut środkowy (gnomiczny, centralny) (Tales z Miletu 639-548 r. p.n.e.)

W tym odwzorowaniu nie zakładamy z góry warunku na zniekształcenia. Obraz powierzchni kuli otrzymujemy jako rzut, którego środek jest w środku kuli.

Korzystając z rysunku wyznaczymy funkcję r(p). Będzie ona równa:

A więc funkcje odwzorowawcze tego odwzorowania będą miały postać:

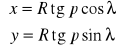
W takim przypadku będzie możliwe odwzorowanie jedynie dla punktów, których

Skale w kierunkach głównych oraz zniekształcenia w tym odwzorowaniu wyniosą:

- wydłużenie w kierunku południków,

- wydłużenie w kierunku równoleżników.

Zniekształcenie kąta będzie równe:

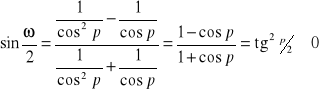
czyli
- kąty ulegają zmniejszeniu.

Skala pola będzie równa:
- powiększenie pola powierzchni.

W rzycie środkowym koła wielkie (ortodromy) odwzorowują się jako linie proste.

Rzut stereograficzny (wiernokątny) (Hipparch ok. 130 r. p.n.e.)

Warunkiem wiernokątności odwzorowania jest równość skal w kierunkach głównych:

czyli

- jest to równanie różniczkowe o rozdzielonych zmiennych

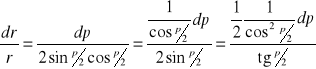
Stałą C wyznaczymy z warunku by równik odwzorował się jako koło o promieniu 2R

A więc funkcje odwzorowawcze tego odwzorowania będą miały postać:

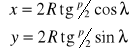
Obraz punktu w rzucie stereograficznym można uzyskać również geometrycznie

Cechą charakterystyczną rzutu stereograficznego jest to, że wszystkie koła odwzorowują się również jako koła.

Skale w kierunkach głównych wyniosą:

- wydłużenie w kierunku południków,

- wydłużenie w kierunku równoleżników,

Jak widać skale te są sobie równe.

Skala pola będzie równa:

- powiększenie pola powierzchni.

Możemy powiedzieć, że w odwzorowaniu stereograficznym kąty są bez zniekształceń natomiast długości ulegają powiększeniu podobnie jak pola powierzchni.

Obraz półkuli mieści się w kole o promieniu 2R.

4.2.2 Odwzorowania azymutalne nieperspektywiczne

Odwzorowanie równoodległościowe Postela (Postel 1510-1581, Vespucci 1524, Mercator 1569)

W tym przypadku założymy, że długości w kierunku południków nie ulegają zniekształceniu:

założenie to prowadzi do równania:

Dla punktu p=0 stała C wyniesie C=0, stąd:

A więc funkcje odwzorowawcze tego odwzorowania będą miały postać:

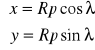
Geometryczna interpretację tego wzoru

przedstawia rys. 5:

Skale w kierunkach głównych oraz zniekształcenia kątów, długości i pola powierzchni wynoszą:

- zachowanie długości w kierunku południków,

- wydłużenie w kierunku równoleżników,

Zniekształcenie kąta wyniesie:

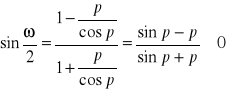
czyli
- kąty ulegają powiększeniu.

Skala pola będzie równa:
- powiększenie pola powierzchni.

W tym odwzorowaniu można przedstawić całą kulę ziemską, obraz półkuli mieści się w kole o promieniu
.

Odwzorowanie równopolowe Lamberta (Lambert w 1772 r.)

Zakładamy w tym przypadku, że skala pola jest równa jedności stąd:

Wstawiając wyrażenia na a i b otrzymujemy:

Jest to równanie różniczkowe rzędu pierwszego. Przez rozdzielenie zmiennych otrzymujemy:

Stałą C wyznaczymy z warunku, że r=0 dla p=0

i dalej przekształcając otrzymujemy

A więc funkcje odwzorowawcze tego odwzorowania będą miały postać:

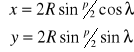
Wyznaczymy następnie skale w kierunkach głównych

- skrócenie w kierunku południków,

- wydłużenie w kierunku równoleżników,

Zniekształcenie kąta wyniesie:

- co oznacza, że
czyli
- kąty powiększają się.

Skala pola będzie równa:

- czyli pola powierzchni nie ulegną zniekształceniu.

W tym odwzorowaniu można przedstawić całą kulę ziemską, obraz półkuli mieści się w kole o promieniu
.

4.2.3 Odwzorowania azymutalne ukośne i poprzeczne

Omawiane wyżej odwzorowania normalne są szczególnym przypadkiem odwzorowania ukośnego. Punkt główny (G) w odwzorowaniu ukośnym nie pokrywa się z biegunem (B) lecz znajduje się w dowolnym punkcie na powierzchni kuli. Wyprowadzone wzory odwzorowań normalnych można wykorzystywać w przypadku odwzorowania ukośnego pod warunkiem zastąpienia współrzędnych (λ,p) współrzędnymi azymutalnymi (α,δ) (Rys. 7)

Związek między współrzędnymi azymutalnymi (α,δ) i geograficznymi (ϕ,λ) wynika z trójkąta sferycznego GBP (Rys.8)

(..)

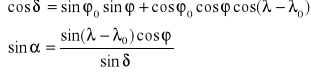
Wzory kolejnych (omawianych wyżej) odwzorować azymutalnych w przypadku odwzorowań ukośnych będą miały postać:

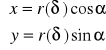
gdzie funkcja r(δ) odpowiada funkcji r(p) z odwzorowań normalnych np. dla odwzorowania

azymutalnego, ukośnego Lamberta będą miały postać:

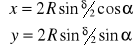
Skale w kierunkach głównych

- skrócenie w kierunku południków,

- wydłużenie w kierunku równoleżników,

Zniekształcenie kąta wyniesie:

- co oznacza, że
czyli
- kąty powiększają się.

Skala pola będzie równa:

- czyli pola powierzchni nie ulegną zniekształceniu.

W przypadku odwzorowania poprzecznego punkt główny znajduje się na równiku kuli (ϕ₀=0°). Wtedy wzory (...) ulegną uproszczeniu.

4.2.4 Odwzorowania azymutalne sieczne

W odwzorowaniach azymutalnych siecznych płaszczyzna przecina kulę stykając się z nią wzdłuż tzw. okręgu sieczności (rys. 8). Sieczność uzyskuje się poprzez nadanie odwzorowaniu dodatkowej skali liniowej mniejszej od jedności. Między skalami liniowymi w odwzorowaniu siecznym i stycznym zachodzi związek:

gdzie m₀ jest dodatkową skalą powodującą sieczność. Z powyższego związku wynikają zależności dotyczące zniekształceń w odwzorowaniach siecznych. Niezależnie od rodzaju odwzorowania, odwzorowania sieczne charakteryzują się bardziej równomiernym rozkładem zniekształceń liniowych w stosunku do odwzorowań stycznych. Odpowiednio dobrana skala m₀ dla danego obszaru odwzorowania umożliwia uzyskanie najmniejszych (co do wartości bezwzględnych) zniekształceń liniowych.

Z równania (..) wynika również związek między współrzędnymi X,Y w odwzorowaniu stycznym i siecznym:

Kartografia matematyczna. Odwzorowania azymutalne kuli.

10

B

P′

r(p)

Rys. 1

y

x

r(p)

P′

B

R

B

P′

r(p)

Rys. 2

P

R

B

P′

r(p)

Rys. 3

P

R

B

P′

r(p)

Rys. 4

P

R

R

B

P′

r(p)

Rys. 5

P

r(p)

B

P′

r(p)

Rys. 6

P

r(p)

α

G

Rys. 8

90°-ϕ

P′

B

P(ϕ,λ)

B

P

G(ϕ₀,λ₀)

Rys. 7

P

B

G

δ

90°-ϕ

90°-ϕ₀

α

δ

α

δ

P(ϕ,λ)

90°-ϕ

G(ϕ₀,λ₀)

Rys. 8

B

P

G

P′

B

okrąg styczności

---