4. Elementy teorii powierzchni. Odwzorowanie powierzchni na powierzchnię.

4.1. Powierzchnie

Powierzchnią w geometrii różniczkowej nazywamy zbiór punktów przestrzeni, których położenie określa w sposób jednoznaczny ciągła i dwukrotnie różniczkowalna w pewnym obszarze (D) funkcja wektorowa dwóch niezależnych od siebie parametrów u i v

Równanie:

(1)

nazywamy wektorowym równaniem powierzchni.

W układzie ortokartezjańskim równanie powierzchni ma postać:

(2)

lub inaczej

(3)

Krzywe na powierzchni określone równaniem postaci

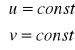
(5)

nazywamy liniami stałego parametru lub odpowiednio liniami współrzędnych u i v danego przedstawienia parametrycznego powierzchni. Linie te tworzą na powierzchni tzw. siatkę Gaussa (rys. 2) lub siatkę współrzędnych Gaussa.

4.2 Pierwsza forma kwadratowa powierzchni

chcemy znaleźć długość ds.

Wyznaczymy w tym celu różniczkę
wektora
:

(6)

Wygodniej jest posłużyć się wyrażeniem ds.²

(8)

Wstawiając wyrażenie (6) do wzoru (8) otrzymujemy

(9)

- I forma kwadratowa powierzchni (10)

gdzie:
,
,

Wyrażenie (10) nosi nazwę pierwszej formy kwadratowej powierzchni, zaś wyrażenia E,F,G są jej współczynnikami.

4.3 Kat między krzywymi na powierzchni

Kat miedzy krzywymi jest kątem między stycznymi do krzywych w punkcie przecięcia.

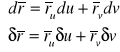
(12)

Z definicji iloczynu skalarnego mamy (Rys. 4)

(13)

Po wstawieniu do (13) wzorów (10) otrzymujemy

(14)

Jako szczególny przypadek wyznaczymy kąt między liniami parametrycznymi:

Wtedy dla l₁ (linii parametrycznej v=const) mamy

dla l₂ (linii parametrycznej u=const) mamy

Po wstawieniu do (14) otrzymujemy

(15)

Stąd wniosek, że siatka linii parametrycznych jest ortogonalna gdy F=0.

Kąt między dowolną krzywą a linią parametryczną będzie równy:

(18)

gdzie wyrażenie
nazywamy kierunkiem k.

Kąt na powierzchni zależy od współczynników I formy kwadratowej i od kierunku.

4.4 Odwzorowanie powierzchni

Rozpatrzymy dwie powierzchnie dane równaniami:

Jeżeli znajdziemy związki między parametrami

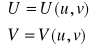
lub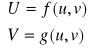
(19)

czyli funkcje odwzorowawcze to możemy powiedzieć, że odwzorowanie jest określone. Wtedy będziemy mieć dwie powierzchnie odniesione do tych samych parametrów.

Zapiszemy to krótko:

,
(20)

Def. odwzorowania

Odwzorowaniem jednej powierzchni na drugą nazywamy każdą jednoznaczną i wzajemną odpowiedniość punktową między powierzchnią, którą przyjmujemy za powierzchnię oryginału a powierzchnią, którą przyjmujemy za powierzchnię obrazu.

Funkcje (19) powinny spełniać dwa warunki:

- powinny być klasy C² (dwukrotnie różniczkowalne i ciągłe),

- jakobian odwzorowania musi być różny od zera (funkcje są wtedy niezależne):

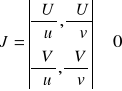
(21)

W odwzorowaniach regularnych: obrazem punktu jest punkt, obrazem krzywej jest krzywa, koła jest koło, obszaru jest obszar.

4.5 Pierwsze twierdzenie Tissota

W dowolnym regularnym odwzorowaniu jednej powierzchni na drugą istnieją dwa kierunki prostopadłe, które odwzorowują się również jako kierunki prostopadłe. Kierunki te nazywamy kierunkami głównymi

Przy odwzorowaniu wiernokątnym każda para kierunków prostopadłych odwzorowuje się jako para kierunków prostopadłych.

Twierdzenie to posiada ogólniejszą postać:

W dowolnym regularnym odwzorowaniu jednej powierzchni na drugą istnieje (co najmniej jedna) siatka ortogonalna, która odwzorowuje się na siatkę ortogonalną. Siatka ta nazywa się siatką główną.

4.6 Skala odwzorowania

Na obu powierzchniach przyjmiemy siatkę linii parametrycznych pokrywających się z siatką główną (kierunki główne pokrywają się z kierunkami linii parametrycznych).

Skalę odwzorowania definiujemy w sposób następujący:

- elementarna skala długości (29)

Wygodniej jest nam posłużyć się kwadratem skali.

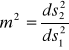
(30)

Jeżeli przyjmiemy, że na obu powierzchniach siatka linii parametrycznych jest siatką główną to skale w kierunkach głównych będą równe skalom w kierunkach linii parametrycznych.

Dla linii v=const. (dv=0):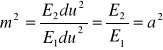
(31)

Dla linii u=const. (du=0):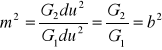
(32)

Skale w kierunkach głównych nazywamy skalami głównymi (a,b)

Dla skali w dowolnym kierunku będzie:

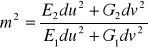
a po przekształceniach:

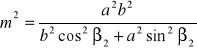
(33)

gdzie a,b skale główne.

Przyjmując następnie: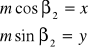

otrzymamy

Jest to równanie elipsy Tissota lub wskaźnicy Tissota.

II twierdzenie Tissota

Obrazem graficznym zniekształceń długości we wszystkich kierunkach wychodzących z jednego punktu powierzchni jest elipsa, której półosie są równe zniekształceniom w kierunkach głównych.

4.7 Zniekształcenia kątów

Na powierzchni S₁ weźmy kąt β₁ i odpowiadający mu kąt β₂ na powierzchni S₂.

,
,

Zniekształcenie kąta definiujemy jako różnicę kątów

Do obliczenia tej różnicy wykorzystamy wzory:

,

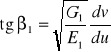
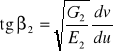
Po przekształceniach będzie:

(35)

Maksymalna wartość różnicy
będzie wtedy, gdy

(36)

(37)

Maksymalne zniekształcenie ω jest równe podwójnej wartości (β₁-β₂)_max.

Jeżeli a=b to wg wzoru (37) zniekształcenie kąta jest równe zeru czyli odwzorowanie jest wiernokątne (równokątne, konforemne)

4.8 Zniekształcenie pola

(38)

Jest to wzór na elementarne pole.

Na powierzchni S₁ bierzemy element pola dP₁ i odpowiadający mu na powierzchni S₂ element dP₂.

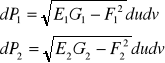
Skalę pola i zniekształcenie pola definiujemy w sposób następujący:

- skala pola,
- zniekształcenie pola

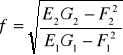
(39)

Przyjmujemy dodatkowo, że mamy siatkę główną czyli, że
i otrzymujemy

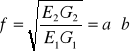
(40)

Jeżeli f=1 to odwzorowanie nazywamy wiernopolowym (równopolowym).

Kartografia matematyczna. Elementy teorii powierzchni. Odwzorowanie powierzchni na powierzchnię.

8

y

x

z

M

S

Rys. 1

Rys. 2

Rys. 9

P

Rys. 4

l₂

l₁

Rys. 3

P

P₁

(S₂)

(S₁)

P₁

P₂

Q₁

Q₂

v

u

Rys. 6

S₂

S₂

Rys. 8

S₁

Rys. 10

S₁

x

y

a

b

---