4.4 Odwzorowania stożkowe

Weźmy stożek styczny do kuli wzdłuż obranego równoleżnika. Punktowi P na powierzchni kuli przyporządkowujemy na pobocznicy stożka punkt P′ według ściśle określonego prawa. Następnie przetniemy stożek wzdłuż wybranej tworzącej i pobocznicę stożka rozwiniemy na płaszczyźnie.

Po rozwinięciu pobocznicy stożka na płaszczyźnie otrzymamy wycinek koła należący do jakiegoś kąta środkowego β mniejszego od 360°.

Definicja

Odwzorowaniem stożkowym normalnym nazywamy odwzorowanie powierzchni kuli na płaszczyznę, w którym obrazem południków są proste przecinające się w wierzchołku S′, obrazem zaś równoleżników są łuki kół współśrodkowych o środku w S′.

Kąty zawarte między południkami na kuli zostały w obrazie zmienione, a mianowicie wszystkie zostały zmniejszone w tym samym stosunku.

Ogólne równania odwzorowań stożkowych mają następującą postać:

gdzie: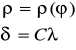
- funkcje współrzędnych ϕ,λ,

q = const,

0 < C < 1

Kartografia matematyczna. Odwzorowanie stożkowe.

1

P′

P

Rys. 1

S

P′

B

S′