1. CZĘŚĆ KONCEPCYJNA

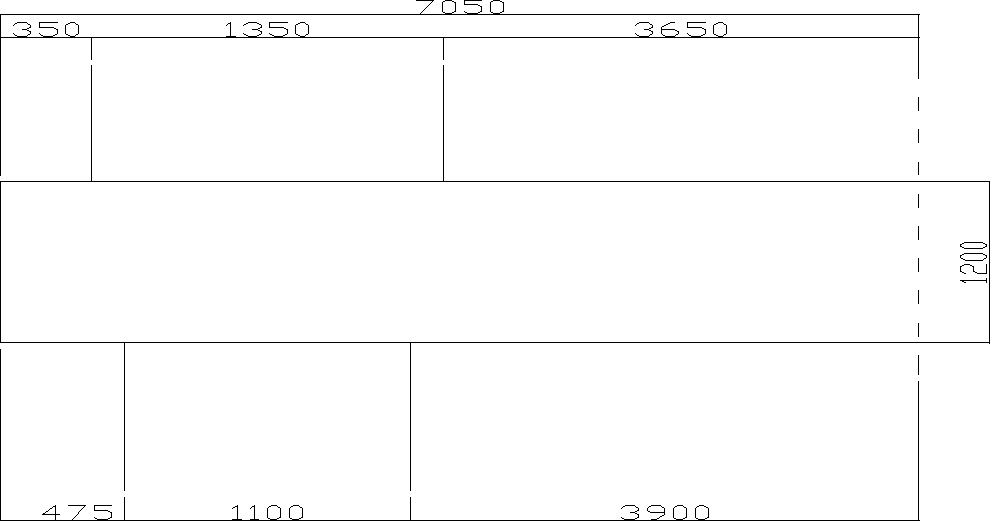
Propozycje podziału na przęsła przedstawia rys. nr 1.

Przekrój poprzeczny przęsła mostowego, oraz koncepcje ukształtowania podpory przedstawia rys. nr 2.

2. ZEBRANIE OBCIĄŻENIA NA WYBRANĄ DO OBLICZEŃ PODPORĘ

ORAZ OBLICZENIE REAKCJI R_B.

1. Zestawienie obciążeń stałych.

Nazwa elementu	Obc. Charakterystyczne	Obc. Obliczeniowe
Konstrukcja niosąca	160 kN/mb	160*1,2=192 kN/mb
Elementy niekonstrukcyjne	80 kN/mb	80*1,5=120 kN/mb
Σ=	gk=240 kN/mb	go=312 kN/mb

2. Zebranie obciążeń zmiennych.

1. Obciążenie równomiernie rozłożone od taboru samochodowego.

-dla klasy obc. A : q_n=4.00 kN/m²

-szerokość jezdni : b=8 m

Wartość charakterystyczna: q_k= q_n*b=4 kN/m²*8 m=32 kN/m

Wartość obliczeniowa: q_o= q_k*γ_f=32*1,5=48 kN/m

2. Obciążenie od pojazdu.

-dla klasy obc. A : K=800 kN

-nacisk na oś: P=200 kN

1. Współczynnik dynamiczny φ.

φ =1,35-0,005L≤1,325

φ=1,35-0,005*28

φ=1,21≤1,325

-charakterystyczna wartość nacisku na oś: P_k=P* φ=200*1,21

P_k=242 kN

-obliczeniowa wartość nacisku na oś: P_o¹=P*φ* γ_f=200*1,21*1,5=363 kN

P_o²=P* γ_f=200*1,5=300 kN

2.2.3. Obciążenie tłumem do obliczeń chodników służbowych.

Do obliczeń dźwigarów głównych i podpór: q_t=2,5 kN/m².

- wartość charakterystyczna: q_tk=2*b₁* q_t=2*0,5*2,5=2,5 kN/m

- wartość obliczeniowa: q_to=2* b₁* q_t* γ_f=2*0,5*2,5*1,3=3,25 kN/m

1. Obciążenie pojazdem klasy 150 wg standardu STANAG 2021




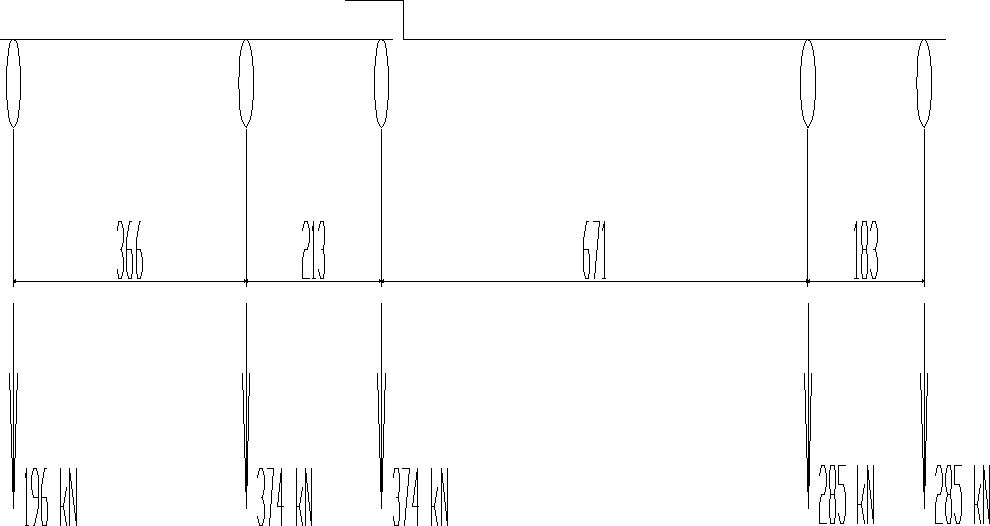
Obc. obliczeniowe (γ_f=1,35)

196*1,35=264,6 kN

374*1,35=504,9 kN

285*1,35=384,75 kN

2.3. Wyznaczenie max. reakcji R_B.

2.3.1 Linia wpływy reakcji R_B [-].




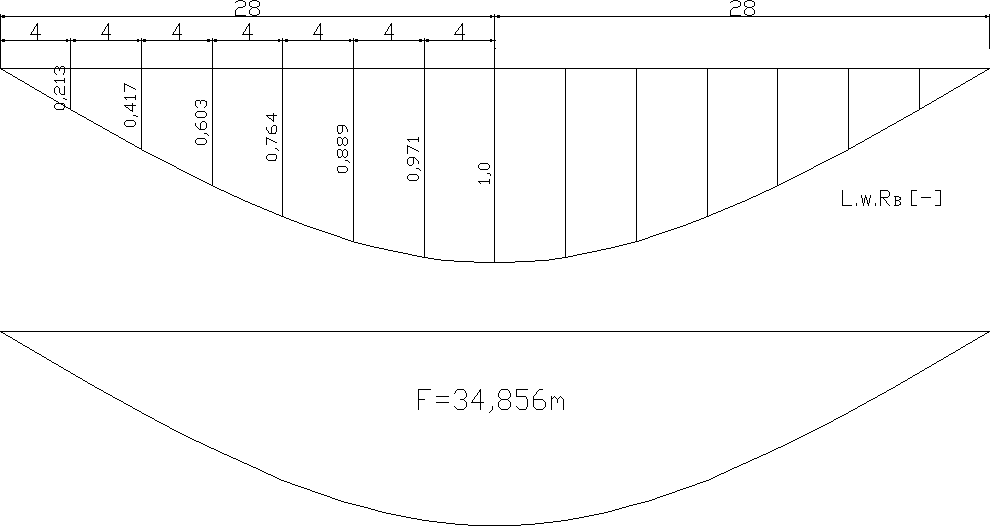
2.3.2. Wyznaczenie reakcji od obciążeń stałych.

-wartość charakterystyczna

R_Bk^s=240kN/m*34,856m=8365,44kN R_Bk^s/2=4182,72kN (2 łożyska)

-wartość obliczeniowa

R_Bo^s=312kN/m*34,856m=10875,072kN R_Bo^s/2=5437,536kN

2.3.3. Wyznaczenie reakcji od obciążeń zmiennych

• Reakcja od obciążenia taborem samochodowym , tłumem i pojazdem K




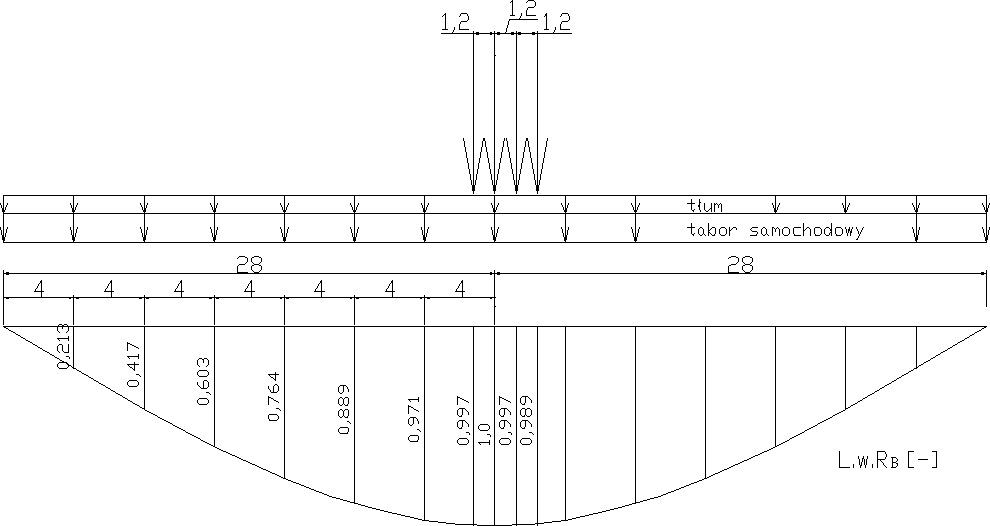
-wartość charakterystyczna

R_Bk^z= P_k*η+q_k*F+q_tk*F

R_Bk^z =242kN*(0,997+1,0+0,997+0,989)+32kN/m*34,856m+2,5kN/m*34,856m=2166,418kN

-wartość obliczeniowa (1-uwzględnia φ; 2-bez uwzględnienia φ)

R_Bk^z /2=1083,209kN (2 łożyska)

R_Bo^z1= P_o¹*η+q_o*F+q_to*F

R_Bo^z1=363kN*(0,997+1,0+0,997+0,989)+48kN/m*34,856m+3,25kN/m*34,856m=3232,199kN

R_Bk^z1 /2=1616,01kN

R_Bo^z2= P_o²*η+q_o*F+q_to*F

R_Bo^z2=300*(0,997+1,0+0,997+0,989)+48kN/m*34,856m+3,25kN/m*34,856m=2981,27kN

R_Bk^z2 /2=1490,635kN

• Reakcja od obciążenia Stanag.







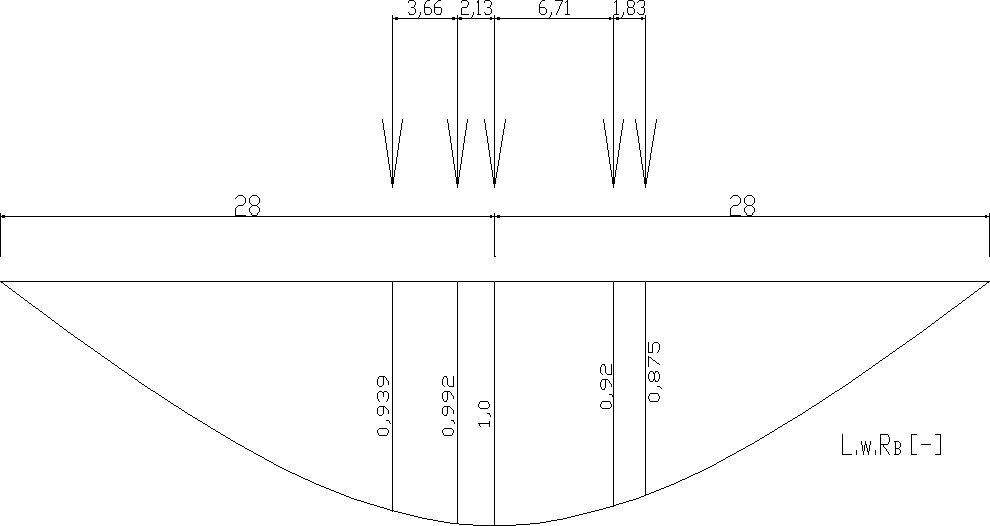
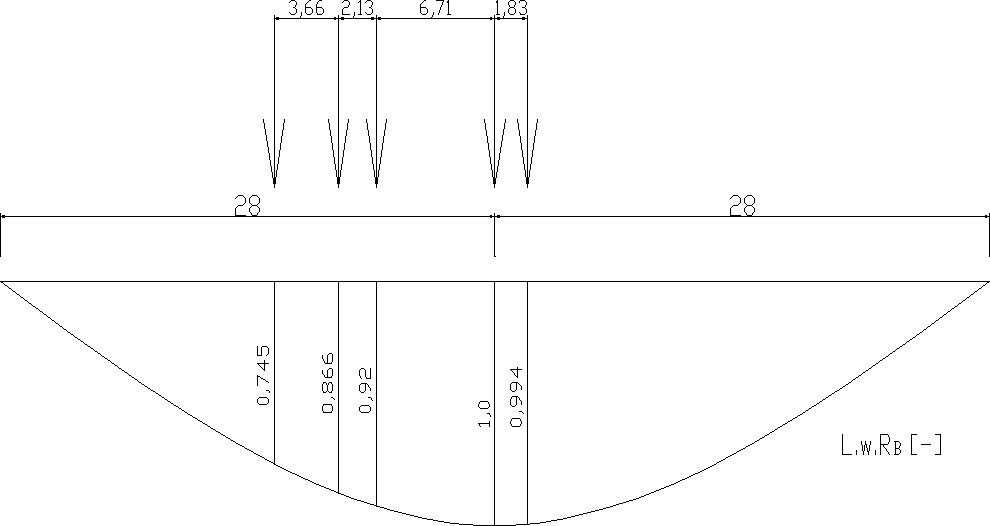
-wartość charakterystyczna

R_{Bk ST}^z=196kN*0,993+374kN *(0,992+1,0)+285kN *(0,92+0,875)=1451,211kN

R_{Bk ST}^z/2=725,606kN (2 dźwigary)

-wartość obliczeniowa

R_{Bo ST}^z=264,6kN *0,993+504,9kN *(0,992+1,0)+384,75kN *(0,92+0,875)=1959,135kN

R_{Bo ST}^z/2=979,568kN (2 dźwigary)

Pojazd przekazuje obciążenie na 2 dźwigary (szerokość pojazdu 4060mm, jedzie środkiem jezdni).

2.3.4. Łączna wartość reakcji R_Bi przekazywana na pojedyncze łożysko.

• Ciężar własny konstrukcji + tłum + tabor samochodowy + pojazd K.

-wartość charakterystyczna

R_Bk= R_Bk^s+ R_Bk^z=4182,72kN+1083,209kN=5265,929 kN

-wartość obliczeniowa

R_Bo¹= R_Bo^s+ R_Bo^z1=5437,536kN+1616,01kN =7053,546 kN

R_Bo²= R_Bo^s+ R_Bo^z2=5437,536kN+1490,635kN =6928,171kN

• Ciężar własny konstrukcji + pojazd Stanag kl.150

-wartość charakterystyczna

R_Bk= R_Bk^s+ R_BkST^z=4182,72kN+725,606kN=4908,326 kN

-wartość obliczeniowa

R_Bo¹= R_Bo^s+ R_BoST^z=5437,536kN+979,568kN=6417,104 kN

2.4. Wyznaczenie siły poziomej (hamowanie i przyspieszanie taboru samochodowego)

Wartość siły hamowania lub przyspieszanie taboru samochodowego należy przyjmować jako 10% obciążenia q oraz 20% obciążenia K, lecznie mniej niż 1/3K, bez współczynnika dynamicznego. Obciążenie q należy uwzględnić na całej szerokości jezdni i na długości do 20m każdego przęsła.

-wartość charakterystyczna

H_k=0,1*q_k*(20+20)m+0,2*K=0,1*24kN/m*40m+0,2*800kN=256kN <1/3K=266,667kN

-wartość obliczeniowa

H_o=0,1*q_o*(20+20)m+0,2*K=0,1*36kN/m*40m+0,2*800kN=304kN >1/3K=266,667kN

3. PRZYJĘCIE ŁOŻYSKA

Wartość charakterystyczna reakcji wynosi 5265,929 kN i 266,667kN

Przyjęto łożysko garnkowe FX 6000-500

Wymiary H=136mm

A=580mm

B=640mm

Ciężar (kg)=255

4. WYMIAROWANIE CIOSÓW PODŁOŻYSKOWYCH.

Siła przekazywana na pojedynczy cios podłożyskowy

R_B=7053,546 kN+2,05 kN=7056,096 kN

a=780 mm

b=0,45*a=350 mm

a'=580 mm

• Naprężenia ściskające

σ_x=


• Naprężenia rozciągające w ciosie podłożyskowym wyznaczono przy pomocy wykresu

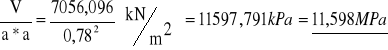
Y. Guyona

(x=b/2=350/2=175mm=0,224a, a'/a=580/780=0,744)

σ_y=0,04* σ_x=0,04*11,598MPa=0,464Mpa

• Siła rozrywająca na którą projektuje się zbrojenie.

F_y= σ_y*0,5a*a=0,464Mpa*0,5*0,78m*0,78m=141,124 kN

• Wyznaczenie pola powierzchni zbrojenia

σ=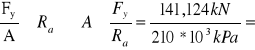
6,72*10^-4 m²=6,72 cm²

Przyjęto 4 siatki o oczkach 100x100mm z prętów φ8 w rozstawie co 80mm(w pionie)

siatki ze stali AI

0,4²*П=0,50 cm² 0,50*7=3,5 cm² 3,5*4=14 cm²

( Ze względów konstrukcyjnych należy uwzględnić 2 siatki w korpusie filara.)

4.1. Sprawdzenie nośności ciosu zbrojonego siatkami na docisk.

• Warunek nośności na docisk elementó zbrojonych siatką zgrzewaną

wg. PN-91/S-10042 ma postać:

N≤α_d*R_d*A_d+k*R_au*A'a (74)

σ_dmin=11,598Mpa (naprężenie dociskowe w ciosie)

σ_dmax=V/(П*580²/4)= 7056,096 *1000 N/264208mm²=26,707MPa (n. doc. w łożysku)

α_d=1/3*(2+σ_dmin/σ_dmax)=1/3*(2+11,598/26,707)=0,811

R_d-wytrzymałość betonu na docisk; dla elementów zbrojonych: R_d=m_d*R_b1

A_r=0,78*0,78=0,6084m²

A_d=3,14*0,58²/4=0,2642 m²

m_d=
=


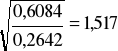
R_b1-wytrzymałość oliczeniowa betony na ściskanie (dla B40 -23,1MPa)

R_d=m_d*R_b1=1,517*23,1=35,043MPa

k=1,5 (dla zbrojenia w postaci siatek zgrzewanych)

n_i-liczba prętów w siatce

l_i-dł prętów w obu kierunkach

A_i-pole przekroju prętó siatki

c-skok siatki

A'a=


R_au=210 MPa

• Sprawdzenie warunku

N≤α_d*R_d*A_d+k*R_au*A'a=0,811*35,043*0,2642+1,5*210*0,0314=17,399MN

N=7,056MN<17,399MN

Warunek nośności na docisk został spełniony.

5. WYMIAROWANIE FILARA

5.1. Koncepcja filara.


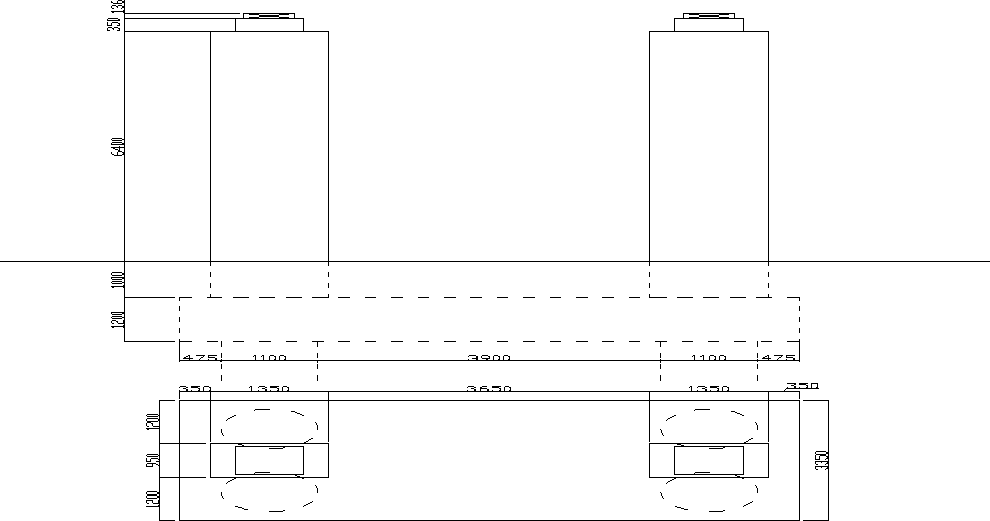
Wartość siły przekazywanej na filar (reakcja bez wsp. dynamicznego + ciężar łożyska

i ciosu)

R_Bo²=6928,171kN

σ_ł=2,05 kN

σ_c=0,78*0,78*0,35*24=5,111 kN

R_Bo=6928,171kN+2,05 kN+5,111 kN=6935,332 kN=6,935 MN

5.2. Sprawdzenie smukłości oraz mimośrodu, na którym działa siła

• Smukłość

λ=L_w/i

L_w=L*μ=(6,4+1)*2=14,8 m

A=0,95*1,35=1,283m²

J_b=0,95*1,35³/12=0,195 m³




λ=14,8/0,39=37,949 >7 (należy uwzględnić wpływ smukłości)

• Mimośród całkowity

e_c=e₀+e₁+e₂+e₃ (42)

e₀-mimośród początkowy

N=R_Bo+G

G=L*A*γ*γ_f=7,4*1,283*25*1,2=284,826 kN

e₀=M/N=0,5H_o*L/N=0,5*266,667*7,4/(6935,332+284,826)=0,137 m

e₁-mimośród przypadkowy, uwzględniający pochylenie siły ściskającej

e₁=max(a/30; 20mm; L/300)=max(0,95/30; 20; 7,4/300)=0,032 m

e₂-niezamieżony mimośród wynikający z nachylenia podpory

e₂=L/150=7,4/150=0,0493 m

e₃-mimośród uwzględniający wpływ odkształcalności drugiego rzędu

e₃<50→ e₃=0

e_c=e₀+e₁+e₂+e₃=0,137+0,032+0,049+0=0,218m

• Rdzeń przekroju dla koła

r=a/6=0,95/6=0,158

e_c/r=0,218/0,158=1,38>1

Wniosek: wystepuje duży mimośród!

5.3. Przyjęcie zbrojenia. Sprawdzenie max naprężeń normalnych w filarze.

N=R_Bo=6935,332 kN

• Założono zbrojenie w postaci prętów #24 x 13

A_a=58,811 cm²

y₀₁= y₀₂= y₀=0,5*0,95=0,475 m

a=0,05 m

h₁=d-a=0,95-0,05=0,90 m

• Beton B35 (E_b=34,6 GPa) Stal AI St3SX-b (E_a=205 GPa)

n= E_a/ E_b=205/34,6=5,925

• Sprawdzenie naprężeń normalnych

Wyznaczenie strefy sciskanej x.

-suma momentów sił wewnętrznych względem punktu przyłożenia siły

x³+3x²(e-y₀)+6n/b[A_a(e-y₀+a)+ A_a(e+y₀-a)]x-6n/b[A_a*a(e-y₀+a)+ A_a*h₁(e+y₀-a)]=0 (Z1-17)

x³+3x²*(0,218-0,475)+6*5,925/1,35*[58,8*10^-4*(0,218-0,475+0,05)+ 58,8*

10^-4*(0,218+0,475-0,05)]*x-6*5,925/1,35*[58,8*10^-4*0,05*(0,218-0,475+0,05)+ 58,8*

10^-4*0,90*(0,218+0,475-0,05)]=0

x³-0,771x²+0,0674x-0,088=0

x₁=0,82m

x₂=-0,24m

x₃=-0,24m

• Sprawdzenie naprężeń w betonie.

e_c/r=1,66

λ=39,467 → β=0,817

σ_b=


σ_b=
=


R_B=R_B1*β=20,2*0,817=16,503 MPa


Warunek został spełniony.

• Sprawdzenie naprężeń w stali rozciąganej.

σ_b=


σ_b=


σ_b=9,319MPa<β*R=0,817*280=228,76MPa Warunek został spełniony.

6. WYMIAROWANIE OCZEPU

• Zbrojenie oczepu w kierunku poprzecznym.




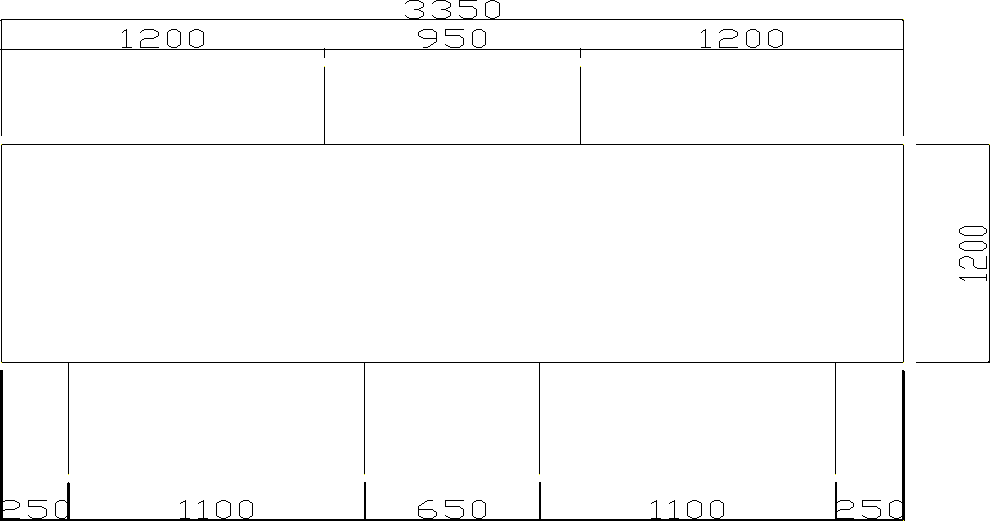
zbrojenie dołem







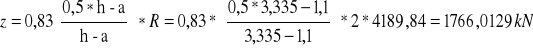
Przyjęto #24 co 22,5cm (14szt.)→A_s=63,33cm²

zbrojenie górą







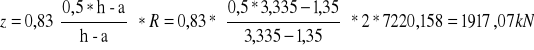
Przyjęto #24 co 223cm (16szt.)→A_s=72,37cm²

• Zbrojenie oczepu w kierunku podłużnym.




Zbrojenie dołem




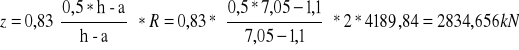
stal 18G2A R-wyt. na rozciąganie = 280MPa




Przyjęto #24 co 23cm nad palem, co 42 między palami(24szt.)→A_s=104,05cm²

Zbrojenie gurą




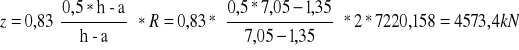
stal 18G2A R-wyt. na rozciąganie = 280MPa




Przyjęto #24 co 15cm nad słupami, co 28 między słupami (36szt.)→A_s=163,86cm²

---