1.1. METODY OBLICZEŃ W ŚWIETLE POTRZEB GEODEZYJNYCH.
1.1.1. Zasady ogólne
1.1.2. Pisownia liczb
1.1.3. Sprawdzenie obliczeń
1.2. OBLICZENIA NA LICZBACH PRZYBLIŻONYCH
1.2.1. Zapis liczb przybliżonych
1.2.2. Zaokrąglanie liczb przybliżonych
1.2.3.Ocena dokładności funkcji liczb przybliżonych
A. Metoda podwójnego obliczania
B. Metoda różniczki zupełnej
C. Prawo przenoszenia sie błędów
D. Metoda wielocyfrowości - reguły Kryłowa-Bradisa
1.3. JEDNOSTKI MIAR
1.3.1. Miary kątowe
A. Miara stopniowa
B. Miara gradowa
C. Miara tysięczna
D. Miara czasowo-kątowa
E. Miara łukowa
1.3.2. Zamiana wartości kątów
A. Zamiana stopni na grady i odwrotnie
B. Zamiana stopni na tysięczne i odwrotnie
C. Związek miary stopniowej z miarą czasową
D. Zamiana stopni na radiany i odwrotnie
E. Zamiana gradów na tysięczne i odwrotnie
F. Związek pomiędzy miarą gradową a łukową
G. Zamiana tysięcznych na miarę łukową i odwrotnie
1.3.3. Funkcje trygonometryczne małych kątów
R o z d z i a ł 1
WYBRANE ZAGADNIENIA TEORII BŁĘDÓW
W ZASTOSOWANIU DO OBLICZEŃ I POMIARÓW
1.1. METODY OBLICZEŃ W ŚWIETLE POTRZEB GEODEZYJNYCH.
Geodezja jako nauka o Ziemi zawiera w sobie szereg dyscyplin towarzyszących. Dyscypliny te wyrosły na bazie potrzeb nauki i techniki w formie samoistnych działów, które w programie dydaktycznym stanowią odrębne przedmioty. Jeżeli dla jakiegokolwiek pomiaru podstawowym warunkiem jego realizacji są instrumenty do pomiaru wg określonej metody, to sposób poprawnego opracowania tych wyników wymaga znajomości metod liczenia. Wyniki pomiaru pewnych wielkości wchodzą zwykle w skład danych liczbowych do funkcji określanych nie zawsze wprost, ale najczęściej w formie pośrednich rozwiazań. Również możliwość wielokrotnego rozwiązania zadania wymaga wprowadzenia uzasadnionych ograniczeń. Właśnie ten dział geodezji, bazujący głównie na wykonywaniu dużej ilości obliczeń związanych z obserwacjami, musiał się szczególnie rozwinąć dla zaspokojenia potrzeb, wprowadzając do numerycznego opracowania wyniku eksperymentu wiele nowych technik rachunkowych.
We wszystkich dociekaniach eksperymentalnych mamy do czynienia z wartościami przybliżonymi. Dokonując jakiegokolwiek pomiaru, na przykład mierząc powierzchnię skrzydła samolotu odpowiednim przyrządem, otrzymujemy na ogół wynik przybliżony, o czym można się przekonać powtarzając pomiar. Wynikiem takiego pomiaru są wartości liczbowe, które wobec nie znanej wartości rzeczywistej są liczbami przybliżonymi. Podobnie, dokonując złożonych operacji rachunkowych na liczbach uzyskanych z pomiarów, otrzymujemy również wynik przybliżony. Od właściwego doboru stopnia przybliżenia użytych liczb zależy uzyskany wynik, a zarazem bezpośrednie źródło poznania określonych wielkości fizycznych. Rachunki wykonywane na liczbach przybliżonych nie mogą bowiem mieć większych dokładności, niż na to pozwala dokładność danych.
Opracowywane wyniki pomiarów, jako oparte na działaniu z liczbami przybliżonymi, należą do numerycznego opracowania danych liczbowych. Mimo że obecnie coraz częściej sięga się do doskonalszych narzędzi, jak elektroniczne środki obliczenowe, to nie zawsze jest pożądane czy możliwe, aby uruchamiać tak skomplikowane narzędzia rachunków. Dlatego konieczne jest zaznajomienie się również z prostymi, lecz często bardziej dostępnymi i praktyczniejszymi metodami techniki obliczeniowej.
Technika obliczeniowa na liczbach przybliżonych daje wprawdzie wyniki przybliżone, które jednak w pewnych fazach opracowania albo wystarczają, albo pomagają w wyszukiwaniu dokładności wartości.
Obliczenia są częścią procesu goedezyjnego i przedstawiają pewnego rodzaju zadanie matematyczne, w którym jako dane najczęściej występują wielkości pochodzące z pomiarów. Na ich podstawie wyznacza się wartości wielkości nieznanych, związanych z danymi przez ściśle określone zależności matematyczne.
Podobnie jak w matematyce, każde zadanie geodezyjne może być rozwiązane liczbowo (analitycznie, rachunkowo) lub rysunkowo (graficznie). W określonych warunkach sposoby graficzne, zwłaszcza półgraficzne, dostarczają wyników dostatecznie dokładnych i dlatego w praktyce posługujemy się nimi z dużym pożytkiem. Większość zadań geodezyjnych rozwiązuje się jednak liczbowo, zwłaszcza przy obecnym rozpowszechnieniu elektronicznych środków obliczeniowych.
Wydajność pracy i dokładność wyników zależy od warunków, w jakich wykonuje się obliczenia, tzn. na stanowisku roboczym w terenie, w samochodzie sztabowym w miejscu pomiaru, czy też w pracowni obliczeń, jak równeż od środków użytych do obliczeń. Wydajność pracy zależy nie tylko od mniej lub więcej zautomatyzowanego sposobu obliczeń, ale również od technicznego przygotowania rachmistrza, jego podejścia do pracy, systematyczności i skrupolatności oraz przestrzegania ustalonych zasad, które postaramy się omówić.
1.1.1. Zasady ogólne
Przed przystąpieniem do obliczeń rachmistrz powinien dokładnie zapoznać się z zadaniem i ustalić sobie tok pracy. Jeżeli nasuwa się jakaś wątpliwość, powinien zajrzeć do podręcznika i przypomnieć sobie teoretyczną stronę zagadnienia.
Kolejność obliczeń najlepiej jest ująć w odpowiedni schemat (wzór, formularz) rachunkowy, który daje tę korzyść, że całość obliczeń jest przejrzysta oraz ułatwia sprawdzenie i korzystanie z danych w dalszej fazie robót lub przy późniejszych pomiarach. Dobrze opracowany formularzz ułatwia też prawidłowe i bezbłędne wykonywanie obliczeń, a więc przyczynia się do zwiększenia wydajności pracy.
W wyniku obliczeń geodezyjnych musimy otrzymać wartości wolne od błędów rachunkowych. Bezbłędne liczenie wymaga jednak, obok pewnych uzdolnień rachmistrza i nabytej przez niego wprawy, również należytej znajomości związków istniejących między wielkościami danymi i szukanymi, znajomość ta umożliwia bowiem kontrolowanie obliczeń we właściwym czasie. Jeżeli w toku obliczeń zauważy się jakieś niezgodności, to trzeba zaraz szukać błędu, bo może się rozszerzyć zakres obliczeń poprawkowych i zmarnuje się wtedy więcej czasu.
Warunkiem nieodzownym do zredukowania ilości omyłek jest posługiwanie się w obliczeniach cyframi czytelnymi. Należy też uważać na porządkowe i ujednolicone pisanie liczb, tzn. na pisanie ich odpowiednio co do miejsca jednych pod drugimi oraz dzielenie liczb wielocyfrowych na znormalizowane grupy. Obliczenia powinny być prowadzone od razu na czysto, przepisywanie bowiem jest dodatkowym źródłem omyłek.
Ważnym zagadnieniem jest właściwa dokładność obliczeń. Używanie wielu cyfr bezużytecznie komplikuje pracę, często nie dając w zamian żadnych korzyści w postaci lepszych wyników. Ponadto, taka czy inna dokładność obliczeń powinna być dostosowana do potrzeb praktycznych.
1.1.2. Pisownia liczb
Dla zmniejszenia możliwości popełnienia błędów rachunkowych powinno się liczby pisać jednolicie, w sposób uporządkowany, nie zaniedbując tej zasady również przy obliczeniach pomocniczych.
Do oddzielenia cześci ułamkowej od liczby całkowitej używa się przecinka, umieszcza się go u podstawy ostatniej cyfry liczby całkowitej, na przykład 426,34. Jeżeli dla jasności chcemy podać, że jest to liczba mianowana, to odpowiedni symbol pisze się za ostatnią napisaną cyfrą, na przykład 38,8 cm albo 0,388 m. Ta sama zasada obowiązuje też przy pisaniu wartości kątów w układzie dziesiętnym (gradowym), na przykład 125,489g. W przeciwiństwie do tego, wartości kątów wyrażone w starym podziale koła, ponieważ chodzi tu o układ sześćdziesiątkowy (a nie dziesiętny), pisze się w grupach danego rodzaju, a więć 1050645,5.
Często występują liczby stanowiące mały ułamek, na przykład arc 1 = 0,000 001 570 796. Dla skrócenia pisowni piszemy wtedy tylko cyfry znaczące, traktując pierwszą z nich jako liczbę całkowitą i za pomocą kropki w środkowej wysokości cyfr zaznacza się mnożenie przez 10 z wykładnikiem ujemnym wyrażającym liczbę opuszczonych zer. Tak więc mamy arc 1 = 1,570796 10-6.
Jeżeli chce się zaznaczyć, że ostatnia cyfra danej liczby nie jest już pewna, to pisze się ją w mniejszej wysokości lub obniżoną, na przykład 4678.
Dla większej czytelności i łatwiejszego zachowania porządkowanej pisowni, należy liczby wielocyfrowe pisać w grupach trzycyfrowych, licząc od przecinka w lewą i prawą stronę. Na przykład: 3,141 592 653 6; 6 366,197 72; 1 000 000.
Grupy oddziela się między sobą małymi przerwami (spacjami) i nie wolno w tym celu używać kropek. Jeżeli do obliczeń lub wykazów używa się gotowych druków, posiadających liniaturę pionową, pisze się poszczególne grupy w odpowiednich kolumnach. W wykazach kątów lub powierzchni stosuje się kolumny oparte na wyjątku, bowiem stopnie, minuty i sekundy, podobnie jak hektary, ary i metry kwadratowe, stanowią odrębne grupy znaczeniowe.
1.1.3. Sprawdzenie obliczeń
Sprawdzenie obliczeń polega na otrzymaniu tych samych wyników drogą niezależnego rachunku różnymi metodami (np. raz analitycznie, drugi raz graficznie), przy czym oba obliczenia mogą być wykonane przez tego samego wykonawcę albo też wykonują je niezależnie dwaj wykonawcy na tzw.„dwie ręce”, posługując się tymi samymi wzorami lub odpowiednio przekształconymi, co oczywiście jest pewniejsze. Nie są to jednak jedyne sposoby uzyskiwania prawidłowych wyników, można bowiem w pełni zabezpieczyć się przed błędami nie rozwiązując zadania dwukrotnie, lecz stosując odpowiednie kontrole wewnętrzne i szereg kontrolnych czynności pośrednich.
Przed grubymi błędami, powstałymi np. na skutek przyjęcia niewłaściwych danych, powstania przed liczbą błędnego znaku, omyłkowego umieszczenia przecinka itp., ustrzeże nas bardzo dobre sprawdzenie wyniku na rysunku lub wykresie, a nieraz nawet zwykłe szacowanie.
Ze względu na wyjątkowe znaczenie, jakie posiada stałe zabezpieczenie się przed błędami, w rachunkach geodezyjnych wykrystalizowały się pewne sposoby kontroli i pewne typy sprawdzianów. Jednym sposobem kontroli jest dwukrotne niezależne rozwiązanie całego zadania (od początku do końca) przez jednego rachmistrza, a w pewnych wypadkach na „dwie ręce”. Inny sposób kontroli polega na tym, że zadanie rozwiązuje się tylko jeden raz przy stosowaniu szeregu sprawdzianów wewnętrznych, a druga osoba, sprawdza dokładnie pierwszy etap pracy, mianowicie przyjęcie właściwych danych i poprawne ułożenie zadania oraz pewne decydujące etapy. Niekiedy sam wykonawca może uzyskać kontrolę zupełną, jeżeli po zakończeniu obliczeń podstawi otrzymane wartości końcowe do zależności wyjściowych.
1.2. OBLICZENIA NA LICZBACH PRZYBLIŻONYCH
Liczbą przybliżoną, o znanym przybliżeniu, nazywa się taką liczbę x , dla której będzie spełniona nierówność
![]()
(1.1)
gdzie: x - nieznana dokładna (prawdziwa) wartość liczby,
x0 - znana wartość przybliżona danej liczby,
![]()
x - znany błąd wartości przybliżonej xo, zwany „błędem
krańcowym”, „granicą błędu” lub „błędem bezwzględnym”.
Liczba przybliżona jest znana, gdy znany jest przedział, w którym się ona znajduje.
1.2.1. Zapis liczb przybliżonych
Liczby przybliżone zapisuje się ten sposób, by błąd krańcowy nie przekraczał połowy jednostki ostatniej, zapisanej cyfry.
W ten sposób zapis x = 165,86 oznacza, że
![]()
a więc x mieści się w przedziale
165,855 ![]()
x ![]()
165,865
Wartość błędu krańcowego wynosi tu ![]()
Pisząc = 3,14, widzimy od razu, że
3,14 - 0,510-2 ![]()
![]()
3,14 + 0,510-2
błąd krańcowy zaś wynosi tu ![]()
= 0,510-2.
Wartość błędu krańcowego na ogół zapisuje się pod postacią
![]()
(1.2)
gdzie k jest ujemną lub dodatnią liczbą całkowitą.
Jeżeli liczbę przybliżoną zapisze się zgodnie z przyjętą zasada, to będzie ona zawierać wszystkie cyfry pewne, łącznie z ostatnią.
Zgodnie z ustaleniem, że błąd graniczny charakteryzuje się odpowiednim zapisem, nie wolno dopisywać zbędnych cyfr, które mogłoby sugerować większą dokładność niż faktycznie istniejąca. Pisząc np. l = 15 km, stwierdza się tym samym, że l jest liczbą przybliżoną o błędzie krańcowym ![]()
l = 0,5 km.
Jeżeli jednak napisze się l = 15 000 m, to błąd krańcowy wynosi ![]()
l = 0,5 m. Widzimy, że dwie formalnie równe wartości: l = 15 km i l = 15 000 m,zapisane jako liczby przybliżone, mają różne błędy krańcowe. Dlatego też liczbę a = 314,657 48, o której wiemy, że ma tylko 5 początkowych cyfr pewnych, zapiszemy w postaci a = 314,66 lub a = 31 46610-2. Podobnie gdy liczba całkowita b = 165 784 645 ma sześć początkowych cyfr pewnych, zapiszemy ją następująco:
b = 165 784103 . Jej błąd krańcowy jest równy ![]()
b = 0,5103.
Zamiast mówić „liczba ma n poczatkowych cyfr pewnych”, używa się zwrotu „liczba ma n cyfr znaczących pewnych”.
Liczby przybliżone charakteryzuje się ilością cyfr znaczących. Cyframi znaczącymi są wszystkie cyfry liczb oprócz zer położonych na lewo od pierwszej różnej od zera cyfry.
Podane niżej liczby mają następujące ilości cyfr znaczących:235,56 - 5 cyfr znaczących,
1 357,00 - 6 cyfr znaczących,
0,467 - 3 cyfr znaczących,
500,014 - 6 cyfr znaczących,
6 000,000 - 7 cyfr znaczących,
0,005 - 1 cyfra znacząca.
Zera występujace na końcu liczb mogą mieć dwojakie znaczenie: mogą wskazywać rząd wielkości liczby oraz charakteryzować jej dokładność wyrażoną ilością cyfr znaczących.
Dla włściwej interpretacji ustalono konwencję specjalnego zapisu liczb przybliżonych. Dzięki niej można określić dokładność bez osobnego podawania błędu czy ilości cyfr dokładnych. Napisana liczba 8,456 ma cztery cyfry dokładne. Jeżeli liczba 120 000 ma tylko trzy cyfry dokładne, to niedokładne zera zastępuje się odpowiednią potegą liczby 10, pisząc 120103 lub też 1,20105, a dla zaznaczenia, że liczba 0,2 ma cztery cyfry dokładne, pisząc 0,2000.
Konwencja powyższa nie dotyczy jednak obliczeń pomocniczych, gdzie nieraz wpisuje się więcej cyfr znaczących danej liczby przybliżonej, niż ma ona dokładnych, aby nie powiększać błędów wynikających z działań przybliżonych. Te zapasowe cyfry, maskujace właściwą dokładność liczb występujących w rachunku, nie powinny jednak wprowadzać liczącego w błąd. W tym celu zaleca się zapisywać cyfry zapasowe mniejszym pismem.
1.2.2. Zaokrąglanie liczb przybliżonych
Operując liczbami przybliżonymi, spotykamy się często z koniecznością ich zaokrąglania w przypadkach, gdy dokładność danych lub obliczanych liczb przewyższa potrzebną nam dokładność. Liczby przybliżone zaokrąglamy przestrzegając zasady, by błąd krańcowy nie przekraczał połowy jednostki ostatniego miejsca liczby zaokrąglonej. W myśl tego:
a) Ostatnią, pozostawioną cyfrę zwiększamy o 1, gdy pierwsza z odrzuconych cyfr jest większa niż 5.
b) Ostatnią cyfrę pozostawiamy bez zmiany, gdy pierwsza z odrzuconych cyfr jest mniejsza niż 5.
c) Jeżeli pierwsza z odrzuconych cyfr jest równa 5 i nie następują po niej inne cyfry niż zera, ostatnią cyfrę, gdy jest nieparzysta, zwiększamy o jedność, gdy jest parzysta - pozostawiamy bez zmiany.
d) Jeżeli pierwsza z odrzuconych cyfr jest równa 5, lecz następuje po niej co najmniej jedna cyfra inna niż zero, ostatnią pozostawioną cyfrę zwiększa się o jednostkę.
Niekiedy, w celu prawidłowego dalszego zaokrąglenia liczby przybliżonej, kończącej się cyfrą 5, stawia się nad nią kropkę w przypadku zaokrąglania z niedomiarem lub kreskę w przypadku zaokrąglenia z nadmiarem.
Podane niżej liczby są zapisane w myśl przedstawionych zasad:
12,678 45 12,68
136,453 42 136,453
40,500 40
41,500 42
42,501 43
1.2.3.Ocena dokładności funkcji liczb przybliżonych
Mierzone bezpośrednio wielkości fizyczne służą nam zazwyczaj do obliczania innych wielkości. Tak na przykład dla obliczenia wspołrzędnych punktów mierzy się długości boków i kąty. Wyniki rachunków geodezyjnych, wykonywane na
liczbach przybliżonych, lub ogólniej - wartości funkcji argumentów przybliżonych są także przybliżone. Zagadnienie sprowadza się do obliczenia błędu wartości znanej funkcji, gdy znane są błędy jej argumentów.
Spośród wielu metod wyróżnia się:
a) metodę podwójnego obliczania,
b) metodę różniczki zupełnej,
c) prawo przenoszenia się błędów,
d) metodę wielocyfrowości.
A. Metoda podwójnego obliczania
W tej metodzie oblicza się dwukrotnie zadaną wartość funkcji F = F (x,y,...,s) podstawiając do niej takie liczby przybliżone, by wraz ze znanym błędem przybliżenia (x ![]()
x), (y ![]()
y),...,(s ![]()
s) otrzymać maksymalną oraz minimalną wartość funkcji.
![]()
(1.3)
B. Metoda różniczki zupełnej
Metoda ta wyraża się wzorem rachunku różniczkowego
![]()
(1.4)
gdzie przy założeniu, że ![]()
F = dF oraz ![]()
x = dx, itp., wzór (1.4) jest wtedy różniczką zupełną funkcji F = F (x,y,...,s).
C. Prawo przenoszenia sie błędów
Obliczanie błędu funkcji F (x,y,...,s), oparte o prawo przenoszenia się błędów, scharakteryzowane jest wzorem
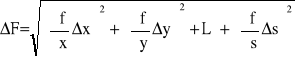
(1.5)
którego pochodzenie oraz właściwą interpretację pozna czytelnik w rozdziale 1.4.
D. Metoda wielocyfrowości - reguły Kryłowa-Bradisa
W odróżnieniu od omówionych metod, metoda wielocyfrowości jest metodą przybliżoną. Metody ścisłe są uciążliwe rachunkowo oraz nie uwzględniają prawdopodobieństwa występowania poszczególnych błędów. Z tych też względów nie nadają się do praktycznego zastosowania. Metoda wielocyfrowości nie określa wprawdzie ściśle błędów mogących wystąpić w rachunku, pozwala jednak na szybkie zorientowanie się, jakiego rzędu wielkości błędów możemy się spodziewać. Właściwego ujęcia tej metody oraz trafnego zebrania zasad obliczeń za pomocą liczb przybliżonych dokonali matematycy - Kryłow i Bradis. Poniżej podane są reguły rachunkowe Kryłowa-Bradisa dla typowych działań:
1. Przy dodawaniu i odejmowaniu liczb przybliżonych należy w wyniku zachować tyle miejsc dziesiętnych, ile ich zawiera liczba o najmniejszej ilości miejsc dziesiętnych.
Uwaga. Miejscami dziesiętnymi liczby nazywamy miejsca położone na prawo od przecinka dziesiętnego.
2. Przy mnożeniu i dzieleniu należy w wyniku zachować tyle cyfr znaczących, ile ich zawiera liczba przybliżona o najmniejszej ilości cyfr znaczących.
Uwaga. Cyframi znaczącymi liczby nazywamy wszystkie jej cyfry, z wyjątkiem zer służących wyłącznie do określania położenia przecinka dziesiętnego.
3. Przy podnoszeniu do kwadratu i sześcianu należy w wyniku zachować tyle cyfr znacących, ile ich zawiera liczba potęgowana.
Uwaga. Ostatnia cyfra potęgi, kwadratu, a zwłaszcza sześcianu jest przy tym mniej pewna od ostatniej cyfry potęgowanej liczby.
4. Przy wyciąganiu pierwiastka kwadratowego i sześciennego w wyniku należy zachować tyle cyfr znaczących, ile ich zawiera pierwiastkowana liczba.
Uwaga. Ostatnia cyfra pierwiastka, w szczególności sześciennego, będzie przy tym pewniejsza od ostatniej cyfry liczby pierwiastkowej.
5. Przy obliczaniu pośrednich wyników rachunku należy brać zawsze o jedną cyfrę więcej, niż to wskazują powyższe zasady.
Uwaga. W rezultacie końcowym tę zapasową cyfrę odrzucamy. Zaleca się ją pisać drobniejszym pismem.
6. Jeżeli niektóre dane zawierają więcej dziesiętnych znaków (w działaniach pierwszego stopnia) lub więcej cyfr znaczących (w działaniach drugiego lub trzeciego stopnia) niż pozostałe, należy je przede wszystkim zaokrąglić, zachowując jedną, zbędną według reguł, cyfrę.
7. Jeżeli dane wyjściowe można brać do rachunku z dowolną dokładnością, wówczas celem otrzymania wyniku o k cyfrach, należy brać dane z taką ilością cyfr znaczących, która zgodnie z regułami 1-4 daje (k+1) cyfr wyniku.
Powyższe reguły oparte są na następującej zasadzie ogólnej: Liczbę przybliżoną należy pisać tak, by wszystkie jej cyfry znaczące, z wyjatkiem ostatniej, były ścisłe. Błąd ostatniej cyfry nie powinien przekraczać średnio jednostki. PRZYKŁAD 1. Obliczyć wartość sumy
S = 12,763 425+6,758+123,425+78,293 62+18,61+21,3625
Zgodnie z regułą 6, przed wykonaniem działania zaokrąglamy liczby pozostawiając 3 miejsca po przecinku, gdyż najmniejsza ilość miejsc dziesiętnych występuje w składniku przedostatnim i wynosi dwa. Po zaokrągleniu sumujemy, otrzymując
S = 12,763+6,758+123,425+78,294+18,61+21,362
Jeżeli uzyskany wynik będzie użyty do dalszych rachunków, to zapiszemy go w postaci S = 261,212 (reguła 5), jeżeli natomiast jest on rezultatem końcowym, to zgodnie z regułą 1 pozostawimy w nim dwa miejsca dziesiętne pisząc S = 261,21. PRZYKŁAD 2. Obliczyć wartość iloczynu
I = 2,63764,298,780,375840,23.
Zgodnie z regułą 6 zaokrąglimy czynniki, pozostawiając w każdym, z wyjątkiem ostatniego, trzy cyfry znaczące. (Ilość cyfr czynnika zawierającego najmniej cyfr znaczących wynosi dwa). Otrzymamy I = 2,6464,298,80,3760,23. Wykonując działania i pamiętając o regule 5, będziemy mieli kolejno
I = 16998,80,3760,23
I = (167102)0,3760,23
I = 62,80,23102
I = 14,4102
Jeżeli wynik stanowi pośrednie stadium rachunku, zapisujemy go w postaci I = 14,4102 . Gdy jest to wynik końcowy, będzie I = 14102.
PRZYKŁAD 3. Obliczając kwadrat (96,4)2 , zapiszemy wynik w postaci 9293 lub 929102 (reguła 3), w zależności od tego, czy liczba bierze udział w dalszym rachunku, czy stanowi wynik końcowy.
PRZYKŁAD 4. Sześcian (0,8935)3 obliczymy, korzystając z reguł 5 i 3. Będzie kolejno (0,8935)3 = 0.798340,8935 = 0,71332 lub 0,7133.
PRZYKŁAD 5. Obliczając wartość pierwiastka kwardatowego z liczby 62,873, zachowamy w wyniku 6 lub 5 cyfr znaczących (reguły: 4 i 5). Będzie więc
![]()
7,92925 lub 7,9292
PRZYKŁAD 6. Obliczając wartość wyrażenia
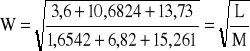
Licznik ma 3 cyfry znaczące pewne, przy czym pozostawiono dodatkową czwartą, gdyż jest to pośredni wynik rachunku L = 3,6+10,68+13,73 = 28,01. Mianownik ma 4 cyfry znaczące pewne, z piątą cyfrą pozostawioną z tych samych względów M = 1,654+6,82+15,261 =23,735. Iloraz będzie więc miał 3 cyfry znaczące pewne, przy czym działania przeprowadzimy na liczbach czterocyfrowych. Ponieważ pierwiastek z liczby mającej trzy cyfry znaczące pewne będzie miał 3 cyfry znaczące pewne, otrzymamy kolejno
![]()
lub 1,09
PRZYKŁAD 7. Wartość wyrażenia
![]()
obliczamy, stosując poznane reguły do kolejno wykonywanych działań. Otrzymamy
SL = 0,36+128,542 = 128,902
SM = 0,3+123.32+902,8 = 1026,42
![]()
lub 5,0
Czasem rezygnuje się ze ścisłego przestrzegania reguł Kryłowa-Bradisa, by zachować w wynikach pośrednich stale tę samą ilość miejsc dziesiętnych, która jest zwykle większa od podanej przez wyżej wymienione reguły. Operowanie liczbami zawierającymi jednakową ilość znaków dziesiętnych znacznie ułatwia obliczenia i zmniejsza możliwość popełnienia błędów rachunkowych.
1.3. JEDNOSTKI MIAR
Pomiar jest to porównywanie danej wielkości z przyjętą jednostką miary. Przy pomiarach geodezyjnych najczęściej określa sie elementy długościowe i kątowe oraz oblicza się w oparciu o nie inne elementy, na przykład współrzędne punktu w przyjętym układzie odniesienia, azymuty wskazanych kierunków itp. Stąd konieczne jest ustalenie jednostek miar długości i kąta. Jednostki te potocznie nazywa się miarami.
Do oznaczania długości w Polsce przyjęto system metryczny. Miarą jednostkową w tym systemie jest metr (oznaczany małą literą m), którego wielokrotności i podwielokrotności są ułożone w systemie dziesiętnym (km, hm, dcm, cm i mm).
Miara kąta płaskiego może być określona w dwojaki sposób.
W pierwszym sposobie jednostką główną jest kąt pełny, tj. kąt środkowy, któremu odpowiada łuk okręgu koła o długości równej jego obwodowi.
Drugi sposób określania kąta płaskiego opiera się na utworzeniu stosunku łuku (ł) koła, odpowiadającego danemu kątowi jako środkowemu, i długości promienia (r).
1.3.1. Miary kątowe
W zależności od sposobu podziału kąta rozróżniamy miarę stopniową, gradową, tysięczną, czasowo-kątową i łukową.
A. Miara stopniowa
Miara stopniowa kąta powstaje przez podział kąta pełnego na 360 części, zwanych stopniami. Podział ten jest dawnego pochodzenia (około 4 000 - 5 000 lat p.n.e.) i dlatego, zgodnie ze stosowanym wówczas w Babilonii sześćdziesiątkowym systemem liczenia, podział wtórny odbywa się według tego systemu. W ten sposód mamy:
![]()
kąta pełnego;
1 = 60 i 1 = 60.
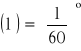
oraz 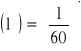
Jako podwielokrotności stopnia mogą być używane dziesiętne części stopnia. System ten nazywany bywa w literaturze systemem mieszanym. Stopień dzieli się tu na 100 minut, a minuta na 100 sekund.
Chcąc przejść z systemu sześćdziesiątkowego na tzw. stopniowo-dziesiętny zachowujemy wartości stopni bez zmian, natomiast minuty i sekundy kątowe przemnażamy przez poniższe zamienniki:
![]()
![]()
Miara stopniowa kąta jest rozpowszechniona niemal we wszystkich gałęziach nauk matematyczno-fizycznych i technice.
B. Miara gradowa
Miara gradowa polega na podziale kąta pełnego na 400 części i stosowaniu, przy dalszym podziale, systemu dziesiętnego. W ten sposób mamy:
![]()
kąta pełnego;
![]()
i ![]()
.
Z powodu wielu cech dodatnich, miara gradowa zdobyła sobie szerokie uznanie w geodezji.
C. Miara tysięczna
Tysięczna jest jedną sześciotysięczną częścią kąta pełnego.
Zapisuje się ją w następujący sposób:
![]()
Jest podstawową miarą stosowaną w artylerii.
D. Miara czasowo-kątowa
Miara czasowo-kątowa powstaje przez podział kąta pełnego w sposób analogiczny do podziału doby na godziny, minuty i sekundy. Mamy więc:
![]()
kąta pełnego;
![]()
i ![]()
Miara czasowo-kątowa znajduje zastosowanie prawie wyłącznie w niektórych zagadnieniach astronomii.
E. Miara łukowa
Dla łukowej miary kąta, zwanej też miarą radialną lub analityczną, jednostką główną jest radian , tzn. kąt płaski zawarty między dwoma promieniami koła, wycinającymi z okręgu tego koła łuk o długości równej promieniowi. Wprawdzie według międzynarodowego układu jednostek miar SI kąt ten określa się skrótem „rad”, będziemy jednak nadal używać oznaczenia , ponieważ to oznaczenie nadal jest wykorzystywane do licznych wzorów, co mogłoby prowadzić do nieporozumień, a nawet błędów. Według matematycznej definicji ![]()
jest to stosunek łuku do promienia r:
![]()
= ł:r .(1.6)
Kątowi pełnemu odpowiada 2 radianów.
Rys.1.1
Łukowa miara kąta ma szerokie zastosowanie nie tylko w matematyce, ale również w zagadnieniach geodezyjnych, zwłaszcza w rachunkach dokładnościowych.
1.3.2. Zamiana wartości kątów
Ze względu na konieczność korzystania z instrumentów pomiarowych posiadających różne systemy miar kątowych, występuje nieraz w praktyce potrzeba przeliczenia wartości kątów z jednego podziału na drugi. Aby przejść ze jednej miary na drugi i odwrotnie, wystarczy zapamiętać podstawową zależność:
![]()
; (1.7)
łatwo bowiem wówczas wyprowadzić wzory zamienne.
A. Zamiana stopni na grady i odwrotnie
Jeżeli przez oznaczymy kąty wyrażone w mierze stopniowej, a przez - te same kąty, ale wyrażone w mierze gradowej, to możemy napisać następujące oczywiste zależności:
![]()
(1.8)
![]()
(1.9)
![]()
(1.10)
a z nich wypływają następujące dwa szeregi wzorów:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 1. Przedstawić kąt = 242142 w mierze gradowej.
g = 241,1111111g + 211,85185c + 423,086cc = 27,06852g
PRZYKŁAD 2. Przedstawić kąt = 27,0685g w mierze stopniowej.
= 0,927,0685g = 24,36165.
Aby wyrazić wartość kąta w układzie sześćdziesiątkowym, trzeba dokonać jeszcze przeliczenia ułamka dziesiętnego, wyrażającego części stopnia (tj....,36165) na minuty i sekundy.
24,36165 -zapisujemy 24 a resztę, tj.0,36165 poddajemy dalszym przeliczeniom; 0,3616560= 21,699 -zapisujemy 21, resztę tj.0,699 poddajemy dalszym przeliczeniom;0.69960= 41,94. Ostateczna wartość kąta = 242141,94.
Istnieje wiele sposobów przeliczenia kątów z miary stopniowej na gradową i odwrotnie.
B. Zamiana stopni na tysięczne i odwrotnie
Przy identycznym toku rozumowania, jak to przeprowadzono wyżej, znajdziemy:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 3. Przedstawić kąt = 242142 w mierze tysięcznej.
tys = 2416.6667+210,2778+420,00463 = 04-06,0291.
PRZYKŁAD 4. Przedstawić kąt = 04-06,0291 w mierze kątowej.
= 0406,02910.06 = 24,3617 = 242142,1.
C. Związek miary stopniowej z miarą czasową
W mierze czasowej za jednostkę przyjmuje się jeden pełny obrót Ziemi dokoła własnej osi, nazywając go dobą. Części pełnego obrotu wyraża się w godzinach, minutach i sekundach, które w tym przypadku mają znaczenie kątów, a nie jednostek miary czasu. Jeżeli dobę podzielimy na 24 godziny, a dalej - zgodnie z systemem sześćdziesiątkowym - ustalimy mniejsze jednostki w postaci minut i sekund miary czasowej kąta, to otrzymamy niezwykle prostą i dogodną zależność z miarą stopniową kąta. Oto ona:
360 = 1d
1 = ![]()
![]()
![]()
![]()
![]()
![]()
D. Zamiana stopni na radiany i odwrotnie
Z relacji, wynikającej z definicji miary łukowej i stopniowej, wyprowadzić można związek pomiędzy obiema miarami
![]()
(1.11)
![]()
(1.12)
Oznaczając wyrażenie ułamkowe literą otrzymamy odpowiednio:
![]()
![]()
![]()
Współczynniki noszą nazwę współczynników zamiany miary łukowej na stopniową. Współczynnik oznacza liczbę stopni, minut lub sekund, jakie się mieszczą w jednym radianie.
![]()
![]()
![]()
![]()
![]()
E. Zamiana gradów na tysięczne i odwrotnie
Wychodząc ze wzoru (1.7) otrzymujemy:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 5. Przedstawić kąt = 27,0685g w tysięcz-
nych.
27,0685g00-15 = 04-06,0275
PRZYKłAD 6. Wyrazić kąt 04-06,028 w mierze gradowej.
04-06,0280,0666667g = 27,0685g
F. Związek pomiędzy miarą gradową a łukową
Do zamiany miary łukowej na gradową i odwrotnie wykorzystuje się współczynniki otrzymując następujące zależności:
![]()
![]()
![]()
![]()
![]()
![]()
gdzie
![]()
![]()
![]()
G. Zamiana tysięcznych na miarę łukową i odwrotnie
Do zamiany wykorzystuje się zależność 2 = 60-00. Z niej otrzymujemy:
00-01 = ![]()
![]()
PRZYKłAD 7. Przedstawić kąt 04-06,03 w mierze łukowej.
04-06,030,00104720 = 0,425195 rad.
PRZYKŁAD 8. Przedstawić kąt 0,425195 rad w tysięcznych.
0,42519509-54,92 = 04-06,03.
1.3.3. Funkcje trygonometryczne małych kątów
W analizie matematycznej udowadnia się, że funkcje trygonometryczne można rozwinąć na następujące szeregi potęgowe:
![]()
(1.13)
![]()
(1.14)
![]()
(1.15)
Kąt ![]()
, występujący po prawej stronie powyższych równań, jest wyrażony w mierze analitycznej (łukowej).
Powyższe rozwinięcia wydają się być bardzo dogodne przy pracach rachunkowych, ale pod warunkiem, że można się ograniczyć do wyrazów w drugiej potędze. Przy takim założeniu powyższe wzory przyjęłyby następującą postać:
![]()
![]()
![]()
![]()
Jasną jest rzeczą, że na skutek odrzucenia dalszych wyrazów rozwinięcia, wzory nie dają ścisłych wartości funkcji trygonometrycznych, lecz wartości przybliżone. Im większy będzie kąt , tym większą wartość będą reprezentować wyrazy odrzucone, a co za tym idzie, z tym mniejszą dokładnością wyznaczone zostaną funkcje trygonometryczne.
Trzeba więc założyć z góry pewną dokładność, z jaką należy obliczyć wartości funkcji trygonometrycznych, a wówczas będzie można określić maksymalne wartości kątów, stanowiących granicę stosowalności tych wzorów.
W odrzuconych wyrazach dominujące znaczenie posiada zawsze pierwszy z wyrazów odrzuconych, gdyż jest w każdym przypadku wielkością o dwa rzędy większą, niż następny z kolei wyraz odrzucony. Dalej zauważamy, że wśród dominujących, największą wartość przedstawia drugi wyraz wzoru (1.15), tj. ![]()
, gdyż wyraźnie przewyższa pierwsze odrzucone wyrazy wzorów (1.14) i (1.13). Nie ulega bowiem wątpliwości, że jest
![]()
Wobec tego wystarczy, aby sprawdzianem nieprzekroczenia założonej dokładności był wyraz ![]()
. Kierujemy się przy tym następującym rozumowaniem: Funkcje trygonometryczne używane są najczęściej przy ocenie dokładności oraz obliczeniach współrzędnych, gdzie oblicza się charakterystyczne iloczyny, których składnikami są bok (długość liniowa) i jedna z funkcji trygonometrycznych. Zakłądając średnią długość boku mierzonego taśmą d=150 m, a błąd pomiaru taśmą rzędu 1 cm, postawimy sobie warunek, aby błąd z tytułu uproszczonego obliczania funkcji trygonometrycznej, nie wpłynął na obliczenie wspomnianego iloczynu w stopniu większym niż błąd pomiaru taśmą, to można uważać takie uproszczone obliczanie funkcji trygonometrycznej za uzasadnione, za wystarczająco dokładne.
Przechodząc do matematycznego zapisu powyższego wywodu notujemy
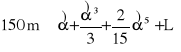
,
który pragniemy zastąpić wyrażeniem,![]()
z tym jednakże zastrzeżeniem, aby pierwszy odrzucony wyraz był mniejszy od 1 cm, czyli, aby
.
Rozwiązjąc tę nierówność otrzymujemy kolejno:
![]()
a następnie
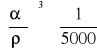
dalej
![]()
i wreszcie
![]()
.
W wyniku naszych rozważań otrzymaliśmy rezultat, który nas poucza, że dla kątów mniejszych niż 321 można stosować wzory uproszczone w miejsce wzorów ścisłych, a powstały z tego tytułu błąd nie przekroczy błędu pomiaru.
W tej sytuacji można przyjąć, że funkcje trygonometryczne małych kątów, tzn. kątów nie większych niż 3, można obliczać ze wzorów przybliżonych:
![]()
, (1.16)
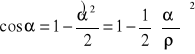
, (1.17)
![]()
, (1.18)
![]()
. (1.19)
Wzory otrzymane drogą analityczną, dadzą się również przedstawić w formie poglądowej, np. na rys. 1.2.
Rysunek 1.2 należy rozpatrywać pod kątem następujących założeń:
1) kąt środkowy jest kątem małym;
2) promień koła jest róny jedności, r=1.
Rys. 1.2
Na podstawie rysunku i powyższych założeń można napisać:
![]()
![]()
![]()
Z rysunku widaćdalej, że wprawdzie s![]()
t, ale dla małych kątów będzie można przyjąć, że
![]()
(1.20)
Zależności (1.20) są identyczne z uprzednio wyprowadzonymi wzorami (1.16) i (1.18).
Zastosowanie wzorów uproszczonych na obliczenie funkcji trygonometrycznych małych kątów przeprowadzimy na kilku przykładach.
PRZYKŁAD 1. Ile wynosi sin 146?
Zgodnie z wzorem (1.16) mamy
![]()
,
a ponieważ 146 = 106, więc
sin 146 ![]()
=0,0308
PRZYKŁAD 2. Ile wynosi kąt x , jeżeli tgx = 0,0444?
Zgodnie z wzorem (1.18) mamy
x = tgx ,
czyli
x = 0,04443438 = 152,6=232,6.
PRZYKłAD 3. Ile wynosi cos 245?
Zgodnie zwzorem (1.17) i uwzględnieniem wartości, danych w zadaniu, piszemy
cos 245 = 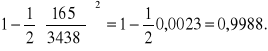
PRZYKŁAD 4. Ile wynosi , jeżeli ctg = 37,5?
Zgodnie z wzorem (1.19) piszemy wprost
![]()
= 131,8.
19
Wyszukiwarka
Podobne podstrony:
Z Obliczenia dla sieci kątowej, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci płaskie, Geodezja i Kartografia, Rachunek Wyrównawczy
Obliczenia na liczbach przybliżonych, Geodezja i Kartografia, Rachunek Wyrównawczy
Ćw. 1 Zastosowanie form rachunkowych Hausbrandta, Geodezja i Kartografia, Rachunek Wyrównawczy
S 7 Równania obserwacji 3, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównanie parametryczne - metoda macierzowa, Geodezja i Kartografia, Rachunek Wyrównawczy
Wagi i błędności, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównania korelat, Geodezja i Kartografia, Rachunek Wyrównawczy
Ściaga RW, Geodezja i Kartografia, Rachunek Wyrównawczy
Z Wyrównanie obserwacji bezpośrednich, Geodezja i Kartografia, Rachunek Wyrównawczy
Równania ogólne poprawek, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia niejednakowo dokładne, Geodezja i Kartografia, Rachunek Wyrównawczy
S 6 Spostrzeżenia bezpośrednie, Geodezja i Kartografia, Rachunek Wyrównawczy
Miary dokładności spostrzeżeń, Geodezja i Kartografia, Rachunek Wyrównawczy
S 5 Błedy wstęp, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci wysokościowe regionalne, Geodezja i Kartografia, Rachunek Wyrównawczy
Podstawowe zasady wyrównania, Geodezja i Kartografia, Rachunek Wyrównawczy
więcej podobnych podstron