STABILNOŚĆ LINIOWYCH UKŁADÓW AUTOMATYKI
Stabilność jest cechą układu, polegającą na powracaniu do stanu równowagi stałej po ustaniu działania zakłócenia, które wytrąciło układ z tego stanu.
Zamknięty układ liniowy będziemy więc uważać za stabilny, jeżeli przy każdej skończonej wartości zakłócenia z(t) i wartości zadanej w(t) oraz dla dowolnych, warunków początkowych, sygnał wyjściowy y(t) dążyć będzie do skończonej wartości ustalonej dla czasu t dążącego do nieskończoności. Niekiedy precyzuje się dodatkowo, że gdy po zaniknięciu, zakłócenia układ powraca do tego samego stanu równowagi co zajmowany poprzednio, wówczas jest stabilny asymptotycznie.
Rys. Schemat zamkniętego układu regulacji automatycznej: O - obiekt regulacji, R - regulator
Przykłady przebiegów y(t) występujących w układach stabilnych i niestabilnych pokazano na rys.
Rys. Przebiegi przejściowe: a) układ stabilny b) układ niestabilny
Jeżeli układ zamknięty opisany jest za pomocą liniowego równania różniczkowego
![]()
lub odpowiadającej mu transmitancji operatorowej
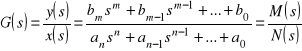
to czasowy przebieg sygnału wyjściowego y(t) po dowolnym zakłóceniu o wartości skończonej opisany jest wzorem o następującej postaci ogólnej (przy założeniu ze równanie charakterystyczne nie ma pierwiastków wielokrotnych ani równych zeru)
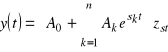
gdzie ![]()
są pierwiastkami równania charakterystycznego układu zamkniętego (mianownika transmitancji operatorowej równego zeru)
![]()
a ![]()
jest wartością zakłócenia. Zakłócenie z(t) może być wprowadzone w dowolnym miejscu układu, w szczególności zakłóceniem może być również zmiana wartości zadanej w(t).
Koniecznym i dostatecznym warunkiem stabilności asymptotycznej układu jest, aby pierwiastki równania charakterystycznego układu zamkniętego miały ujemne części rzeczywiste.
![]()
Wówczas
![]()
gdzie ![]()
jest współczynnikiem o wartości skończonej i układ jest stabilny w podanym uprzednio sensie. Składowe przejściowe wielkości wyjściowej zanikają wówczas do zera przy ![]()
, a pozostaje jedynie składowa ustalona, określona statycznymi własnościami układu. W przypadku pierwiastków zespolonych
![]()
odpowiednie wyrazy sumy 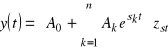
mają postać
![]()
.
Wyrazy te dążą do zera przy czasie ![]()
, jeżeli spełniony jest warunek ![]()
. Jeżeli chociaż jeden z pierwiastków równania ![]()
ma część rzeczywistą dodatnią:
![]()
,
to
![]()
i układ jest niestabilny.
Jeżeli równanie ![]()
ma pierwiastki wielokrotne, to w sumie 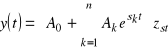
pojawią się wyrazy typu
![]()
W tym przypadku warunek stabilności ![]()
pozostaje również ważny, gdyż funkcja ![]()
rośnie wolniej niż funkcja wykładnicza; zatem dla ![]()
mamy
![]()
.
Jeżeli równanie ![]()
ma pierwiastki w lewej półpłaszczyźnie oraz jednokrotne na osi liczb urojonych (np. jeden pierwiastek zerowy lub parę pierwiastków urojonych sprzężonych), to w układzie będą występować drgania o stałej amplitudzie, określonej warunkami początkowymi. Układ jest wówczas na granicy stabilności, a ściśle mówiąc, nie jest stabilny asymptotycznie. Jeżeli pierwiastki zerowe są wielokrotne, to przebieg y(t) oddala się od początkowego stanu równowagi, układ jest oczywiście niestabilny.
Warunek ![]()
będziemy więc uważać za ogólny warunek stabilności liniowych układów automatyki. Potrzeba ściślejszego rozróżniania rodzajów stabilności wystąpi w układach nieliniowych.
Przy badaniu stabilności układów, których własności dynamiczne opisane są za pomocą równań różniczkowych wyższych rzędów (lub odpowiednich transmitancji), natrafia się na duże trudności przy obliczaniu pierwiastków równania charakterystycznego ![]()
, gdyż jest to równanie algebraiczne tego samego stopnia co rząd równania różniczkowego. Stosuje się wtedy jedno z kryteriów stabilności, tzn. twierdzeń pozwalających ocenić stabilność układu na podstawie wartości współczynników równania charakterystycznego lub przebiegu charakterystyki częstotliwościowej układu otwartego, bez obliczania pierwiastków równania ![]()
. Należy jednak pamiętać, że wszystkie kryteria wywodzą się z warunku podstawowego ![]()
.
KRYTERIUM HURWITZA
Aby wszystkie pierwiastki równania charakterystycznego
![]()
miały części rzeczywiste ujemne, muszą być spełnione następujące warunki:
a) wszystkie współczynniki równania charakterystycznego istnieją i są większe od zera (jest to warunek konieczny, ale nie dostateczny):
![]()
, ![]()
, ..., ![]()
,
b) podwyznaczniki ![]()
, od ![]()
do ![]()
, wyznacznika głównego ![]()
, są większe od zera. Wyznacznik ![]()
, utworzony ze współczynników równania charakterystycznego, ma n wierszy i n kolumn:
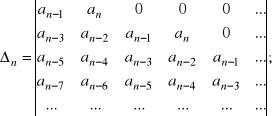
podwyznaczniki ![]()
mają postać:
![]()
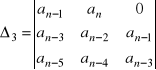
, ...
Powyżej przedstawiono praktyczne sformułowanie kryterium Hurwitza. W oryginalnym sformułowaniu Hurwitza wymaga się, aby wszystkie podwyznaczniki ![]()
, tzn. od ![]()
do ![]()
, były większe od zera. Ponieważ jednak zachodzi
![]()
![]()
,
zatem w przypadku spełnienia warunku a) sprawdzanie dodatniości podwyznacznika ![]()
i wyznacznika głównego ![]()
jest niecelowe.
Jeżeli któryś ze współczynników równania charakterystycznego jest ujemny lub równy zeru albo któryś z podwyznaczników jest ujemny lub równy zeru, to układ jest niestabilny. W przypadku szczególnym, kiedy któryś z podwyznaczników jest równy zeru, równanie charakterystyczne ma, między innymi, pierwiastki czysto urojone i w przebiegu czasowym y(t) występują drgania o stałej amplitudzie. Mówimy wówczas, że układ znajduje się na granicy stabilności (granica stabilności należy do obszaru niestabilnego).
Jeżeli rozpatrywany układ jest niestabilny, kryterium Hurwitza nie pozwala określić, ile pierwiastków równania charakterystycznego ma dodatnią część rzeczywistą.
Przykład 1. Dana jest transmitancja układu zamkniętego
![]()
.
Podać warunki stabilności układu.
Układ jest stabilny, jeżeli spełnione są następujące warunki:
1) ![]()
, ![]()
, ![]()
, ![]()
, ![]()
,
2) ![]()
, a zatem ![]()
,
oraz
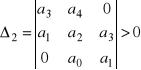
, a zatem ![]()
.
Przykład 2. Zbadać stabilność układu opisanego równaniem różniczkowym
![]()
.
Równanie charakterystyczne układu ma postać:
![]()
.
Układ jest niestabilny, gdyż współczynnik ![]()
. Sprawdzanie znaku współczynników ![]()
, ![]()
, ![]()
oraz podwyznacznika ![]()
jest niepotrzebne.
KRYTERIUM MICHAJŁOWA
Kryterium Michajłowa pozwala na wykreślne sprawdzenie stabilności układu regulacji automatycznej. Podane zostanie wyprowadzenie tego kryterium.
Równanie charakterystyczne układu zamkniętego
![]()
można przedstawić w postaci:
![]()
,
gdzie ![]()
, ![]()
, ..., ![]()
są pierwiastkami tego równania.
Jako zmienną niezależną, s możemy wybrać m. in. zbiór punktów położonych na osi liczb urojonych, wówczas ![]()
i lewa strona równania charakterystycznego przyjmuje następującą postać:
![]()
.
Każdy z czynników ![]()
można przedstawić graficznie jako różnicę dwóch wektorów, wektora ![]()
oraz wektora ![]()
, przedstawiającego k-ty pierwiastek równania charakterystycznego
Rys. Interpretacja graficzna składnika ![]()
Funkcję ![]()
, jako funkcję zmiennej zespolonej, można przedstawić w postaci wykładniczej
![]()
,
gdzie
![]()
oznacza moduł funkcji ![]()
, natomiast
![]()
oznacza argument funkcji ![]()
.
Zmiana argumentu każdego z czynników ![]()
przy pulsacji ![]()
zmieniającej się od ![]()
do ![]()
wynosi ![]()
dla pierwiastka ![]()
położonego w lewej półpłaszczyźnie oraz ![]()
dla pierwiastka ![]()
położonego w prawej półpłaszczyźnie płaszczyzny zmiennej zespolonej s.
Rys. Zmiana argumentu składnika ![]()
przy zmianie ![]()
od ![]()
do ![]()
Jeżeli przyjmiemy, że spośród n pierwiastków równania charakterystycznego {n— m) pierwiastków znajduje się w lewej półpłaszczyźnie, a m pierwiastków znajduje się w prawej półpłaszczyźnie, to zmiana argumentu ![]()
przy zmianie ![]()
od ![]()
do ![]()
wyniesie
![]()
.
Ponieważ warunkiem stabilności jest, aby wszystkie pierwiastki równania charakterystycznego miały ujemne części rzeczywiste, układ będzie więc stabilny, jeżeli ![]()
, tzn. jeżeli
![]()
Warunek ten można uprościć, jeżeli wykażemy, że ![]()
jest krzywą symetryczną względem osi liczb rzeczywistych. Podstawiając w równaniu
![]()
![]()
zapiszemy lewą stronę w postaci
![]()
.
Części rzeczywista i urojona ![]()
wynoszą
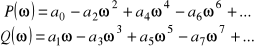
Mamy zatem
![]()
![]()
oraz
![]()
![]()
Wystarczy więc zbadać przebieg jednej gałęzi krzywej ![]()
, dla pulsacji zmieniającej się od 0 do ![]()
.
Kryterium Michajłowa można sformułować ostatecznie następująco:
Układ regulacji automatycznej jest stabilny wtedy i tylko wtedy, gdy zmiana argumentu krzywej ![]()
przy zmianie pulsacji od 0 do ![]()
wynosi ![]()
, gdzie n oznacza stopień równania charakterystycznego
![]()
Krzywą ![]()
nazywa się niekiedy krzywą charakterystyczną lub hodografem Michajłowa.
Z równania
![]()
wynika, że ![]()
dla ![]()
jest liczbą rzeczywistą i ma : wartość ![]()
. Następnie, dla rosnących pulsacji ![]()
, krzywa ![]()
układu stabilnego przechodzi kolejno w kierunku .dodatnim przez n ćwiartek płaszczyzny ![]()
![]()
.
Przykładowe przebiegi ![]()
dla n =1,2, 3, 4 przedstawiono na rysunku.
Rys. Przykładowe przebiegi krzywych ![]()
układów stabilnych
Konstrukcja graficzna wektora ![]()
, którego grot zakreśla krzywą ![]()
wynika z równania
![]()
Otrzymujemy
dla n = l ![]()
,
dla n = 2 ![]()
,
dla n = 3 ![]()
Na rysunku pokazano konstrukcję wektora ![]()
dla ![]()
, w punkcie ![]()
.
Rys. Konstrukcja wektora ![]()
Przykłady krzywych ![]()
układów niestabilnych zostały przedstawione na rysunku.
Rys. Przykładowe przebiegi krzywych ![]()
układów niestabilnych
Wszystkie te krzywe nie spełniają warunku stabilności ![]()
: dla n = 2 ze względu na niewłaściwy kierunek obrotu (zmiana argumentu równa ![]()
), dla n=3 ze względu na ominięcie drugiej ćwiartki płaszczyzny, - dla n = 4 ze względu na zmianę argumentu wynoszącą ![]()
zamiast wymaganej ![]()
. Jeżeli krzywa ![]()
przechodzi przez początek układu, jak pokazano na rysunku dla n = 3, to mówimy, że układ znajduje się na granicy stabilności.
W przebiegu czasowym y(t) występują wówczas drgania niegasnące, a zmiana argumentu ![]()
jest nieokreślona.
Przykład 1. Za pomocą kryterium Michajłowa zbadać stabilność układu zamkniętego, którego transmitancja jest następująca:
![]()
Piszemy równanie krzywej ![]()
![]()
Obliczamy wartości części rzeczywistej ![]()
i części urojonej ![]()
dla kilku ![]()
, zestawiamy wyniki obliczeń w tablicy i sporządzamy wykres.
|
0 |
0,5 |
0,8 |
1 |
2 |
|
2 |
1,5 |
0,72 |
0 |
-6 |
|
0 |
0,875 |
-0,16 |
-2 |
-34 |
Rys. Przebieg krzywej ![]()
Układ jest niestabilny, ponieważ krzywa ![]()
omija drugą ćwiartkę płaszczyzny i zmiana argumentu wynosi (jak widać z rys.)
![]()
,
co jest niezgodne z warunkiem stabilności.
Przykład 2. Na podstawie przebiegu przedstawionej na rys. krzywej ![]()
dla n= 3 udowodnić, że z kryterium Michajłowa wynikają te same warunki stabilności układu jak z kryterium Hurwitza.
Rozwiązanie:
a.
Kierunek przebiegu krzywej jest przeciwny do kierunku obrotu wskazówek zegara, jeżeli
![]()
, ![]()
, ![]()
, ![]()
.
b.
Krzywa przechodzi kolejno przez I, II i III ćwiartkę płaszczyzny, jeżeli ![]()
, tzn. ![]()
. Odpowiada to warunkowi Hurwitza: podwyznacznik ![]()
.
|
97 |
|
Wykład |
Wyszukiwarka
Podobne podstrony:
kon0, automatyka konspekt
kon6, automatyka konspekt
kon9, automatyka konspekt
regulatory, automatyka konspekt
kon13, automatyka konspekt
sprawozdanie automatyka2, studia, V semestr, Automatyka i robotyka, sprawko automaty stabilność
Konspekt wykładów z Podstaw automatyki wykład 5
Konspekt korektywa FIN (Automatycznie zapisany) 2
stabilizatory o dzialaniu ciaglym konspekt sprawozdanie
macierz2, studia, V semestr, Automatyka i robotyka, sprawko automaty stabilność
konspekt automatyka
Wykład 6 Stabilność liniowych układów automatyki (2013)
Stabilność układów automatyki
konspekt wydruk (Automatycznie zapisany)
Ula SPRAWOZDANIE AUTOMATYKA granica stabilnoscix1 emf
Ula SPRAWOZDANIE AUTOMATYKA granica stabilnoscix2 emf
Ula SPRAWOZDANIE AUTOMATYKA granica stabilnoscix0 emf
Ula SPRAWOZDANIE AUTOMATYKA granica stabilnoscix3 emf
więcej podobnych podstron
