Przesuwanie paraboli
Krzywą, która jest wykresem funkcji y = ax2, gdzie a ≠ 0, nazywamy parabolą. Jej wierzchołek leży w początku układu współrzędnych, a kierunek i rozwartość ramion są uzależnione od wartości współczynnika a.
Jeśli a>0, to ramiona paraboli skierowane są do góry .
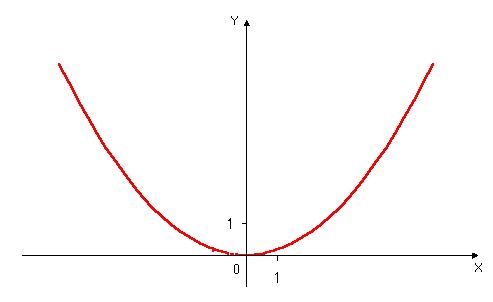
Ramiona paraboli
Rys.1 Wierzchołek paraboli
Jeśli a<0, to ramiona paraboli skierowane są w dół.
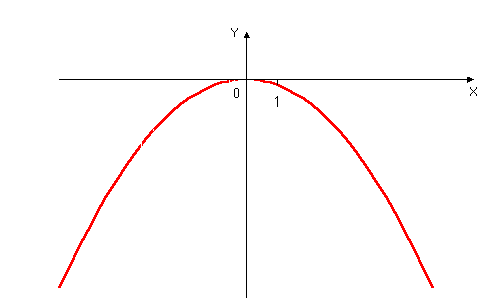
Rys.2
Parabola będąca wykresem funkcji postaci y = ax2 jest symetryczna względem osi y.
Rozwartość ramion paraboli jest uzależniona od wartości współczynnika a - im on jest liczbą bliższą zeru, tym ramiona są bardziej rozwarte.
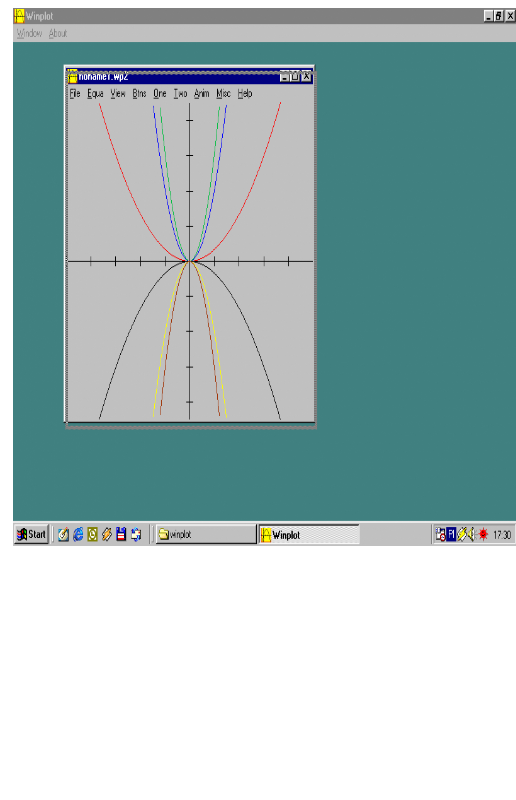
y = 3x2 (czerwony) y = 2x2 (niebieski) y = ![]()
x2 (zielony)
Rys.3
y = -3x2 (czarny) y = -2x2 (żółty) y = -![]()
x2 (bordowy)
Ćwiczenie 1
Wykonaj ćwiczenia A,B str. 220 z podręcznika.
Poniższe parabole przedstawiają funkcję y = -2x2 (niebieska) po przesunięciu:
y = -2(x - 2)2 (czerwona), y = -2(x + 1)2 (zielona), y = -2(x + 4)2 (żółta)
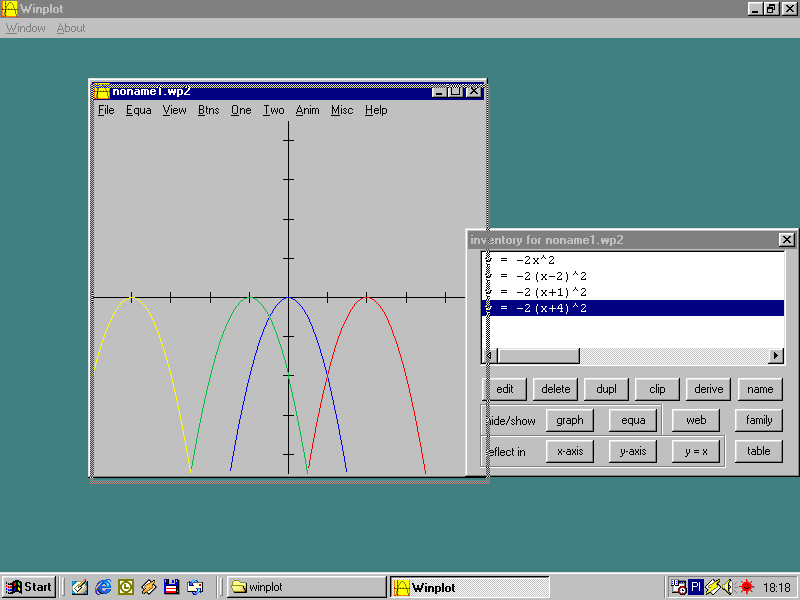
Rys.4
Aby otrzymać takie funkcje musieliśmy dokonać przesunięcia danej paraboli wzdłuż osi x w lewo bądź w prawo. Współrzędne wierzchołka otrzymanych parabol to odpowiednio punkty: (2,0), (-1,0), (-4,0). Jeśli współrzędne wierzchołka paraboli y =2x2 oznaczymy (p,0), wówczas otrzymane parabole możemy ogólnie zapisać wzorem
y = a(x - p)2.
Ćwiczenie 2
Wykonaj ćwiczenie C str. 221 z podręcznika.
Na poniższym rysunku 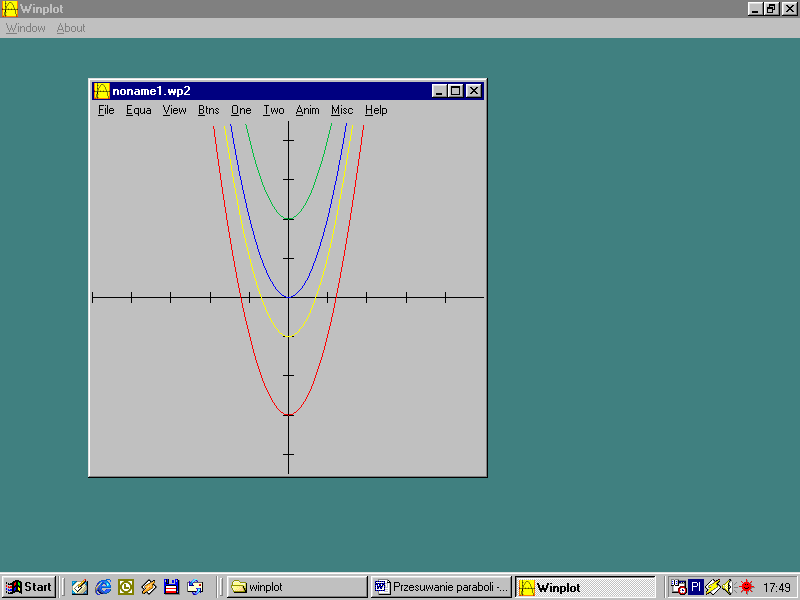
przedstawiono parabolę funkcji y = 2x2 oraz trzy parabole funkcji powstałych w wyniku przesunięcia jej wzdłuż osi y w górę lub w dół.
y = 2x2 - 3, y = 2x2 + 2, y = 2x2 - 1
Rys.6
W wyniku przesunięcia paraboli zmieniły się współrzędne jej wierzchołka. Ogólnie można je zapisać (0,q). Wówczas wzór funkcji po przesunięciu przyjmuje postać
y = ax2 + q.
Ćwiczenie 3
Wykonaj ćwiczenia D, E, F str. 221 z podręcznika.
Jeśli dokonamy przesunięcia paraboli jednocześnie wzdłuż osi x i wzdłuż osi y otrzymamy parabolę będącą wykresem funkcji opisanej wzorem
y = a(x - p)2 + q
gdzie p, q oznaczają współrzędne wierzchołka otrzymanej paraboli.
Poniższy rysunek przedstawia parabolę funkcji y = 2x2 (niebieski) oraz parabole powstałe w wyniku przesunięcia jej:
o 2 jednostki w prawo i 1 jednostkę w dół y = 2(x - 2)2 - 1 (żółty)
o 3 jednostki w prawo i 1 jednostkę w górę y = 2(x - 3)2 + 1 (zielony)
o 1 jednostkę w lewo i 3 jednostki w dół y = 2(x + 1)2 - 3 (czerwony)
rys.7
Zadanie 7 str. 225 (podręcznik)
a>0 i q<0, tzn. że ramiona paraboli są skierowane do góry, a jej wierzchołek znajduje się poniżej osi x. Zatem parabola musi przecinać os x w dwóch miejscach. Pierwsza współrzędna tych punktów to miejsca zerowe funkcji y = a(x - p)2 + q. (patrz : rysunek 7 powyżej - czerwony, żółty)
a ≠ 0 i q = 0
Parabola „dotyka” osi x w jednym miejscu, a ramiona mogą być skierowane do góry lub w dół (rysunek 4)
a<0 i q<0
Ramiona paraboli skierowane są w dół, a jej wierzchołek znajduje się poniżej osi x, zatem funkcja nie ma punktów wspólnych z osią x (cały wykres „leży” poniżej osi x).
Poniższy schemat przedstawia zależności istnienia (i ilości) miejsc zerowych funkcji
y = a(x - p)2 + q
q = 0 a>0 i q<0 a< 0 i q>0
ma jedno miejsce zerowe, gdy ma dwa miejsca zerowe, gdy
Wykres funkcji
ma wierzchołek y = a(x - p)2+q powstał
w punkcie (p,q) dla a ![]()
0 w wyniku przesunięcia
o wektor [p,q]
nie ma miejsc zerowych, gdy
a<0 i q<0 a>0 i q>0
Ćwiczenie 4
Rozwiąż zadania: 1 str. 223, 3,5 str.224 z podręcznika.
Wyszukiwarka
Podobne podstrony:
Procent skladany, Matematyka. Zadania i rozwiązania
Matematyka zadania rozwiązane krok po kroku i inne
nierownosci wielomianowe, Matematyka. Zadania i rozwiązania
Uklady równań, Matematyka. Zadania i rozwiązania
Zastosowania funkcji kwadratowej, Matematyka. Zadania i rozwiązania
Zadania dotyczace funkcji liniowej i jej wlasnosci, Matematyka. Zadania i rozwiązania
Funkcja kwadratowa i jej wlasnosci, Matematyka. Zadania i rozwiązania
Równania kwadratowe z parametrem, Matematyka. Zadania i rozwiązania
Matematyka finansowa zadania z rozwiązaniami 2
Matematyka finansowa - zadania z rozwiązaniami
Przedziały liczbowe - teoria zadania rozwiązania, dokumenty, liceum, matematyka, zbiory
Zadania rozwiązane matematyka kolokwium nr3, Technika Rolnicza i Leśna, Semestr 1, Matematyka
Matematyka finansowa zadania z rozwiązaniami
Zadania z rozwiązaniem - matematyka finansowa, Zadania
więcej podobnych podstron