Układy równa, z których jedno jest stopnia drugiego
Układy równań, z których jedno jest stopnia drugiego i jedno jest stopnia pierwszego rozwiązuje się metodą podstawiania. Oznacza to, że z równania stopnia pierwszego wyznaczamy jedną z niewiadomych i podstawiamy ją do drugiego równania. Wyjaśnię to na kilku przykładach.
Przykłady
Rozwiąż układ równań
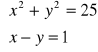
Rozwiązanie
Wyznaczamy z drugiego równania jedną z niewiadomych, np. x = 1 + y. Podstawiamy to wyrażenia do pierwszego równania otrzymując
(1 + y)2 + y2 = 25.
Po zastosowaniu wzoru skróconego mnożenia do nawiasu otrzymujemy
1 + 2y + y2 + y2 =25
2y2 + 2y -25 + 1 = 0
Po uporządkowaniu i obustronnemu podzieleniu przez 2 mamy
y2 + y - 12 = 0
Jest to równanie kwadratowe, które należy rozwiązać, aby wyznaczyć y.
y2 + y - 12 = 0
a = 1 b = 1 c = -12
Δ = b2 - 4ac = 12 - 4⋅1⋅(-12) = 1 + 48 = 49
Ponieważ Δ > 0, więc równanie ma dwa różne rozwiązania
![]()
lub ![]()
![]()
lub ![]()
Wyznaczone wartości podstawiamy do równania x = 1 + y i obliczamy
x1 = 1 + (-4) i x2 = 1 + 3
x1 = -3 i x2 = 4
Rozwiązaniami tego układu równań są pary liczb (-3, -4) i (4, 3).
Rozwiąż algebraicznie i graficznie układ równań
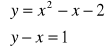
Rozwiązanie
Rozwiązanie algebraiczne
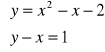
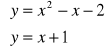
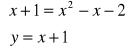
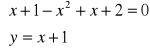
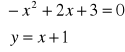
-x2 + 2x + 3 = 0
a = -1 b = 2 c = 3
Δ = b2 - 4ac = 22 - 4⋅3⋅(-1) = 4 + 12 = 16
Ponieważ Δ > 0, więc równanie ma dwa różne rozwiązania
![]()
lub ![]()
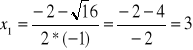
lub 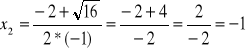
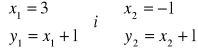
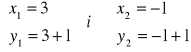
Rozwiązanie : 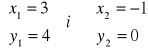
Rozwiązanie graficzne polega na sporządzeniu wykresów obu równań i odczytaniu współrzędnych punktów przecięcia obu wykresów.
Wykresem równania y = x2 - x - 2 jest parabola, gdzie Δ = b2 - 4ac = (-1)2 - 4⋅(-2) = 1 + 8 =9 i stąd współrzędne wierzchołka są równe
p = ![]()
q = ![]()
![]()
lub ![]()
![]()
lub ![]()
Wykresem równania y = x + 1 jest prosta.
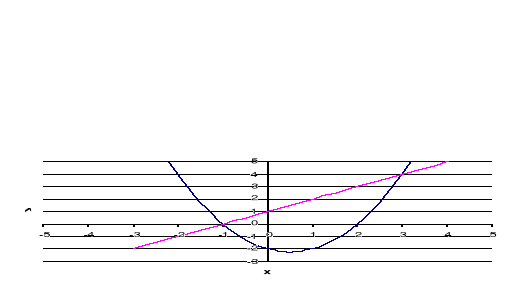
Wykresy obu równań przecinają się w dwóch punktach. Współrzędne tych punktów są zgodne z wynikiem rozwiązania algebraicznego.
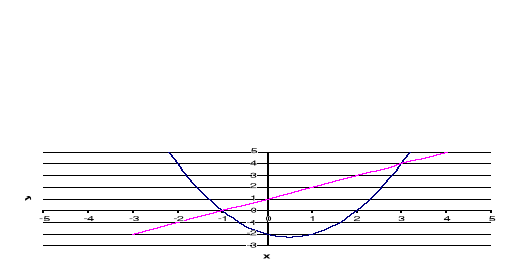
3. Rozwiąż algebraicznie i graficznie układ równań
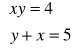
Rozwiązanie
Rozwiązanie algebraiczne
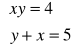
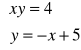
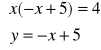
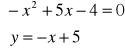
-x2 + 5x - 4 = 0
a = -1 b = 5 c = -4
Δ = b2 - 4ac = 52 - 4⋅(-4)⋅(-1) = 25 - 16 = 9
Ponieważ Δ > 0, więc równanie ma dwa różne rozwiązania
![]()
lub ![]()
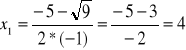
lub 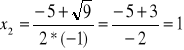
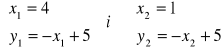
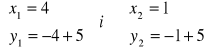
Rozwiązanie : 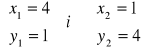
Rozwiązanie graficzne polega na sporządzeniu wykresów obu równań i odczytaniu współrzędnych punktów przecięcia obu wykresów.
Wykresem równania xy = 4 lub y = ![]()
jest hiperbola, natomiast wykresem y + x = 5 jest linia prosta.
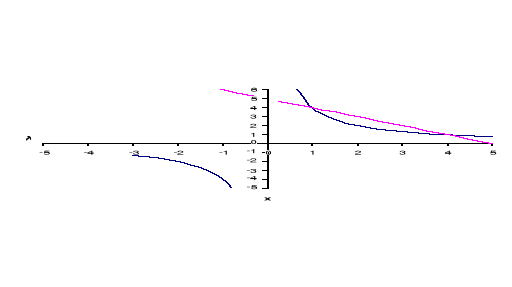
Wykresy obu równań przecinają się w dwóch punktach. Współrzędne tych punktów są zgodne z wynikiem rozwiązania algebraicznego.
Układ równań, z którego jedno jest stopnia pierwszego, a drugie stopnia drugiego może mieć dwa rozwiązania, jedno rozwiązanie albo może ich nie mieć wcale:
układ ma dwa rozwiązania, gdy przez podstawienie sprowadza się do równania kwadratowego, dla którego Δ > 0, a ilustracja graficzna przedstawia wtedy prostą przecinającą krzywą (np. okrąg, parabolę, hiperbolę) w dwóch punktach,
układ ma jedno rozwiązanie, gdy przez podstawienie sprowadza się do równania kwadratowego, dla którego Δ = 0, a ilustracja graficzna przedstawia wtedy prostą mającą dokładnie jeden punkt wspólny z dana krzywą,
układ nie ma rozwiązań, gdy przez podstawienie sprowadza się do równania kwadratowego, dla którego Δ < 0, a ilustracja graficzna przedstawia wtedy prostą i krzywą nie mające punktów wspólnych.
Ćwiczenie 1
Rozwiąż układy równań :
a) 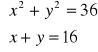
b) 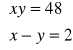
Wyszukiwarka
Podobne podstrony:
Równania kwadratowe z parametrem, Matematyka. Zadania i rozwiązania
UKLADY ROWNAN2, matematyka
Procent skladany, Matematyka. Zadania i rozwiązania
Matematyka zadania rozwiązane krok po kroku i inne
nierownosci wielomianowe, Matematyka. Zadania i rozwiązania
Zastosowania funkcji kwadratowej, Matematyka. Zadania i rozwiązania
Zadania dotyczace funkcji liniowej i jej wlasnosci, Matematyka. Zadania i rozwiązania
Uklady równań-1, Matematyka
Uklady rownan, matematyka
Funkcja kwadratowa i jej wlasnosci, Matematyka. Zadania i rozwiązania
Układy równań 2, Matematyka
Przesuwanie paraboli, Matematyka. Zadania i rozwiązania
Układy równań, Matematyka dla Szkoły Podstawowej, Gimnazjum
macierze i układy równań zadania godsys62u2gplwzfucb2g522gfp5inatbntr3ka GODSYS62U2GPLWZFUCB2G522G
Matematyka finansowa zadania z rozwiązaniami 2
Matematyka finansowa - zadania z rozwiązaniami
więcej podobnych podstron