IMIĘ I NAZWISKO Mariusz Kijak	Ćwiczenie C-2 POMIAR CIEPŁA WŁAŚCIWEGO METODĄ ROZŁADOWANIA KONDENSATORA
ROK I KIERUNEK rok I Fizyka Medyczna
		OCENA	OCENA	OCENA
PROWADZĄCY prof. Krzesińska	DATA PODPIS	DATA PODPIS	DATA PODPIS

1. Cel Ćwiczenia

Wyznaczenie ciepła właściwego powietrza metodą rozładowania kondensatora

2. Część Teoretyczna

Do wyznaczenia ciepła właściwego powietrza, potrzebowałem kondensatora, pojemnika z gazem i spiralą grzejną oraz manometru cieczowego.

Kondensator płaski - przyrząd elektryczny zbudowany z dwóch lub więcej przewodników oddzielonych dielektrykami i mających zdolność gromadzenia ładunków elektrycznych, gdy między tymi płytkami występuje napięcie elektryczne. Kondensator charakteryzuje jego pojemność C, która określa zdolność do akumulacji ładunku elektrycznego. Jeśli kondensator po naładowaniu zostanie odłączony od źródła napięcia to jego ładunek pozostaje stały. Jeżeli zaś pozostaje on cały czas podłączony do źródła prądu o stałym napięciu na zaciskach to rozładowuje się przez opór.

Ciepło właściwe - ilość ciepła potrzebna do ogrzania 1kg danej substancji o 1K.

Ciepło molowe - ilość ciepła, jaka jest potrzebna do ogrzania 1 mola danej substancji o 1K.

Doświadczenie przebiegło w następujący sposób. Pierwszą istotną czynnością było podgrzanie gazu, znajdującego się w szczelnym pojemniku, o stałej objętości (przemiana izochoryczna) do pewnej określonej temperatury T + ∆T. Wraz ze zmianą temperatury zmieniało się ciśnienie (p + ∆p)

Przemiana izochoryczna - Jeżeli gaz jest zamknięty w szczelnym naczyniu, to przy zmianie temperatury jego objętość nie zmienia się, natomiast zmienia się ciśnienie.

Zależność ciśnienia gazu od temperatury zbadał Charles oraz sformułował następujące prawo:

Przy ogrzewaniu gazów w stałej objętości stosunek ciśnienia gazu do jego temperatury pozostaje stały.

gdzie:

p - ciśnienie [Pa]

T - temperatura [K]

Stosując to prawo do wymagań mojego zadania, otrzymałem:

gdzie:

∆p - przyrost ciśnienia [Pa]

∆T - przyrost temperatury [K]

Zmianę temperatury mogłem uzyskać poprzez rozładowanie kondensatora, który uprzednio musiałem naładować, gromadząc energie zwaną energią pola elektrostatycznego

Pole elektrostatyczne - właściwość przestrzeni, wewnątrz której na ładunki działają siły elektrostatyczne, a przewodniki elektryzują się przez indukcję.

Energia pola elektrostatycznego:

gdzie:

U - napięcie kondensatora [V]

C - pojemność kondensatora [F]

Rozładowując kondensator i przepuszczając energię przez spiralę grzejną, w wyniku oporu R, została ona zamieniona na ciepło. Wskutek tej przemiany gaz zgromadzony w pojemniku ze spiralą został ogrzany. Ponieważ jest to przemiana izochoryczna (gdzie V = const) ciepło dostarczone do układu ∆Q jest równe przyrostowi energii wewnętrznej ∆U, to:

gdzie C_v jest ciepłem molowym przy stałej objętości

skąd:

Podstawiając do powyższego wzoru równanie
, (równanie na prawo Charles'a:
) oraz wyznaczając ∆p otrzymałem:

Znając równanie stanu gazu doskonałego:

pV = nRT

gdzie:

p - ciśnienie gazu

V - objętość gazu

n - liczba moli gazu

m - masa gazu

μ - masa molowa gazu

R - stała gazowa [8.3144 J/mol K]

T - temperatura gazu

Gaz doskonały - gaz, którego cząsteczki traktujemy jako pozbawione struktury wewnętrznej punkty materialne. Możemy zaniedbać, tym samym, ich oddziaływanie międzycząsteczkowe i wewnątrzcząsteczkowe.

oraz przekształcając je w następujący sposób:

a następnie podstawiając to wyrażenie do równania ∆p, oraz wykonując wszystkie możliwe uproszczenia otrzymujemy:

wiedząc, że

,

gdzie „a” jest to współczynnik kierunkowy obliczony metodą najmniejszych kwadratów, otrzymujemy wzór na ciepło molowe przy stałym ciśnieniu:

3. Przyrządy pomiarowe

• zasilacz wraz z baterią kondensatorów

• pojemnik z gazem i spiralą grzejną

• manometr cieczowy

4. Przebieg ćwiczenia

1. Sprawdzam, czy przełącznik na kondensatorze jest w położeniu - ładowanie kondensatora. Włączam zasilacz do sieci, a przed tym sprawdzam czy potencjometr jest nastawiony na minimalną wartość.

2. Ustalam napięcie zasilacza U = 12V i ładuję baterię kondensatorów C do tego napięcia.

3. Rozładowuję baterię kondensatorów przez opór R, którym jest spirala grzejna w naczyniu z gazem. Notuję w tabeli zmianę ciśnienia ∆p, odczytaną na manometrze M i napięcie U, do którego naładowałem kondensator.

4. Czekam, aż ciśnienie w zbiorniku zrówna się z ciśnieniem atmosferycznym (∆p = 0), a następnie przełączam przełącznik ponownie do pozycji - ładowanie kondensatora i jeszcze dwukrotnie powtarzam pomiar.

5. Zwiększam napięcie ładowania o 2V i powtarzam czynność, aż do wartości U = 28V. Wyniki pomiarów notuję w tabelce.

6. Mierzę temperaturę otoczenia T i ciśnienie atmosferyczne p.

7. Wyniki pomiarów ∆p = f ( U² ) przedstawiam na wykresie i stosuję metodę regresji liniowej do obliczenia nachylenia a oraz odchylenia standardowego S_a.

8. Obliczam ciepło molowe powietrza C_v oraz jego niepewność maksymalną ∆C_v. Porównuje otrzymany wynik z wartością teoretyczną dla dwuatomowego gazu doskonałego.

5. Wyniki Pomiarów

L.p.	napięcie U [V]	napięcie U^2 [V^2]	ciśnienie ∆p [mm H2O]	ciśnienie hydrostatyczne ∆p [Nm^-2]	ciśnienie hydrostatyczne średnie ∆pśr [Nm^-2]
1	12 12 12	144 144 144	12 12 12	115.3 115.3 115.3	115.3
2	14 14 14	196 196 196	16 16 16	153.8 153.8 153.8	153.8
3	16 16 16	256 256 256	24 24 24	230.7 230.7 230.7	230.7
4	18 18 18	324 324 324	36 36 36	346.1 346.1 346.1	346.1
5	20 20 20	400 400 400	42 42 42	403.7 403.7 403.7	403.7
6	22 22 22	484 484 484	52 52 52	499.9 499.9 499.9	499.9
7	24 24 24	576 576 576	68 68 68	653.7 653.7 653.7	653.7
8	26 26 26	676 676 676	82 82 82	788.3 788.3 788.3	788.3
9	28 28 28	784 784 784	100 100 100	961.4 961.4 961.4	961.4

6. Obliczenia

Obliczam ∆p

Wielkości podane:

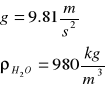
Wielkości obliczone

h (zamieniam jednostki z „mm” w „m”) mm→m

1. 
   

2. 
   

3. 
   

4. 
   

5. 
   

6. 
   

7. 
   

8. 
   

9. 
   

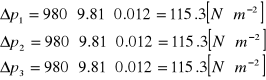
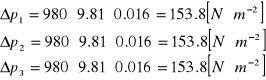
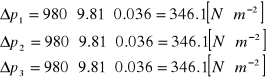
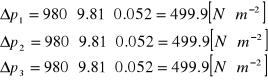
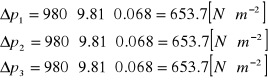
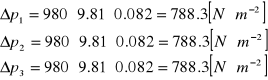
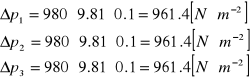
Obliczam ∆p_śr dla każdego pomiaru:

1.

2.

3.

4.

5.

6.

7.

8.

9.

Wykonuję obliczenia i tabelkę do metody regresji liniowej

L.p.	xi U [V]	yi ∆pśr [Nm^-2]	U^2 [V^2]	∆pśr^2 [Nm^-2]	xiyi
1	144	115.3	20 736	13 294.1	16 603.2
2	196	153.8	38 416	23 654.4	301 44.8
3	256	230.7	65 536	53 222.5	59 059.2
4	324	346.1	104 976	119 785.2	112 136.4
5	400	403.7	160 000	162 973.7	161 480
6	484	499.9	234 256	249 900	241 951.6
7	576	653.7	331 776	427 323.7	376 531.2
8	676	788.3	456 976	621 416.9	532 890.8
9	784	961.4	614 656	924 290	753 737.6
∑	3 840	4 152.9	2 027 328	2 595 860.5	2 284 534.8

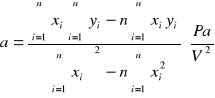
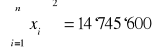
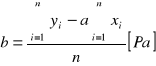
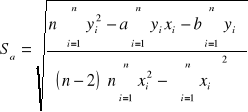
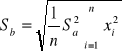
Wykonuje podstawienia i obliczam:

a = 1.31795 [Pa/V²]

b = -100.9 [Pa]

S_a = 0.038 [Pa/V²]

S_b= 17.76 [Pa]

Obliczam ciepło molowe powietrza:

Wielkości stałe oraz podane przez instrukcje:

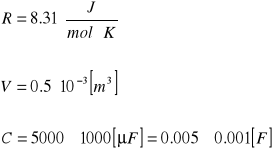
Wielkości obliczone:

a = 1.31795[Pa/V²]

Niepewność C_v

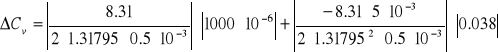
7. Wnioski

• Na podstawie danych z tablic zamieszczonych w „Podstawy termodynamiki technicznej” L. Pastucha E. Milczarek:

C_v=20.735[J/mol K]

• Obliczona przeze mnie wartość C_v odbiega znacznie od wartości tablicowej.

• Pomiary, które wykonałem są obarczone pewnymi niepewnościami, które w istotny sposób mogły wpłynąć na wyniki.

• Odczyty napięcia oraz zmiany ciśnienia nie są dokładne. Spowodowane jest to niedoskonałością ludzkich zmysłów.

• Ciężko było odczytać idealną zmianę ciśnienia ponieważ zachodziła ona dość szybko co uniemożliwiało idealny odczyt.

• Powodem niedokładności mogą być też straty ciepła (pochodzącego od energii naładowanej baterii kondensatorów) do otoczenia.

1

---