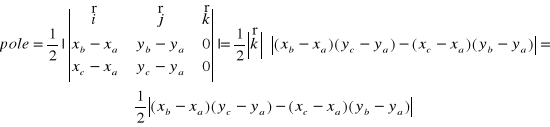
Pole trójkąta to iloczyn wektorowy wektorów odpowiednich boków trójkąta np:

Wektor
to wersor dlatego jego długość jest równa jedności tj.:

gdzie symbol oznacza | | - wartość bezwzględną tj. jeśli wyznaczana wartość

jest ujemna zapisujemy ją jako

Oznacza to, że zmieniliśmy znak wyrażenia na przeciwny.

W przypadku, gdy jest ono dodatnie to:

.

Wyrażenia te można dodatkowo uprościć np.

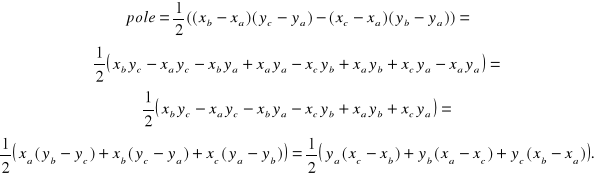
Powyższe wzory można uogólnić dla dowolnego wielokąta.

Zauważmy funkcja pole zależy od sześciu zmiennych

W naszym przypadku wektor pochodnych cząstkowych jest następujący

.

Sprawdzić czy zależności dla pola są prawidłowo wyprowadzone.

Jeśli tak to wyznaczmy wszystkie pochodne znając tylko współrzędne punktów trójkąta.

Błąd pola określimy z zależności:

- to wektor wierszowy, a
kolumnowy pochodnych cząstkowych:

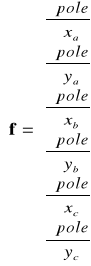
Rozważając przypadek błędów boków trójkąta weźmy pod uwagę bok a.

Długość
boku a to

Jest to funkcja czterech zmiennych
.

Ponieważ nie zależy ona od
to pochodne cząstkowe względem tych zmiennych są zerami.

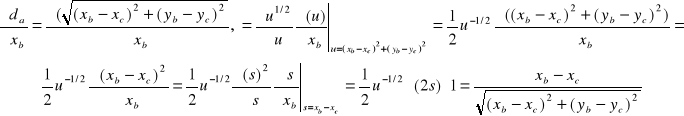
Dlaczego tak wyznaczyliśmy tą pochodną.? Dlatego, że jest to funkcja złożona (nawet podwójnie złożona).

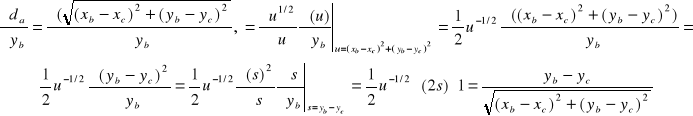
Analogicznie

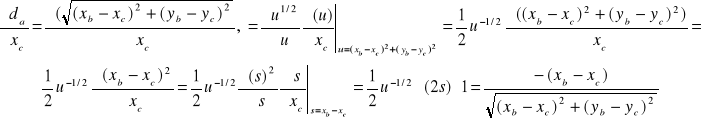
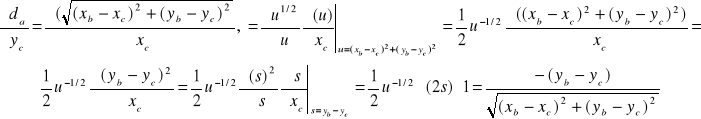
Podsumowując:

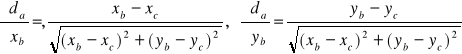
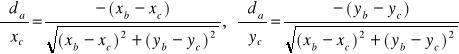
Jeśli wybralibyśmy inny odcinek np. b to pochodne wyznaczamy z analogicznych wzorów. Zastępując odpowiednio współrzędne. Przykładowo:

,

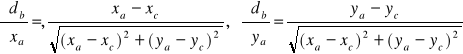
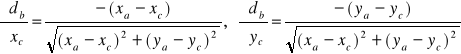
Widać, że w porównaniu z poprzednimi w tych zależnościach zamieniliśmy tylko
na
i
na
.

Jak widać pochodne cząstkowe boku trójkąta (odcinka) można wyznaczyć znając współrzędne jego końców. Tutaj

Macierz kowariancyjna jest taka jak poprzednio. Stąd

.

Uzupełnienie

W poniższym zapisie przyjęto
,
, itd.

.

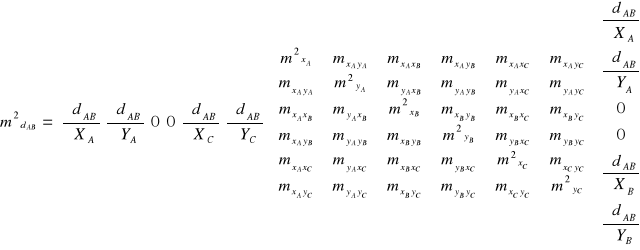
W przypadku błędów azymutu i kątów trzeba wyznaczyć pochodne cząstkowe odpowiednich funkcji arctg. Ponieważ

to

Kąt
jest różnicą kątów (azymutów)
i
.

Kąt
jest funkcją sześciu zmiennych (azymut czterech)

Różniczkując funkcję
względem zmiennej
otrzymujemy:

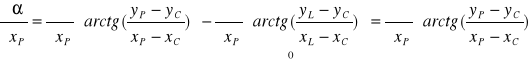
Zauważmy, że pochodna cząstkowa drugiego wyrazu względem
jest zerem, ponieważ argument tej funkcji nie zależy od zmiennej
. Funkcja
jest złożona względem
(
traktujemy jako stałe). Dlatego

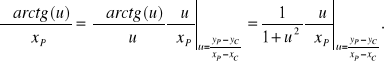
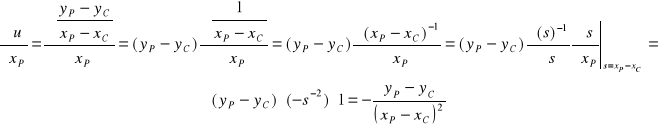
Stąd

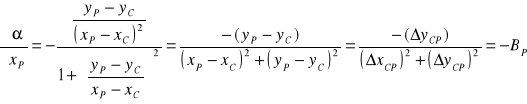
Wartość pochodnej oznaczono tutaj symbolem
. Podobnie postępujemy w przypadku

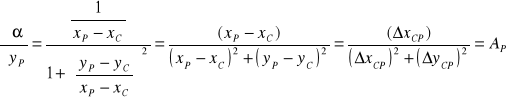
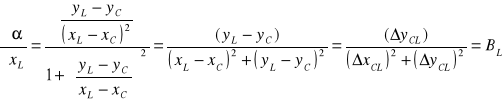
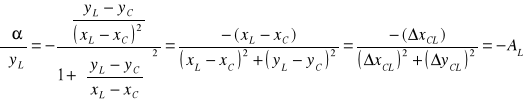
Można pokazać, że

Wynika to z następujących obliczeń:

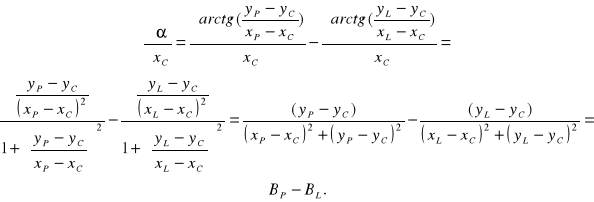
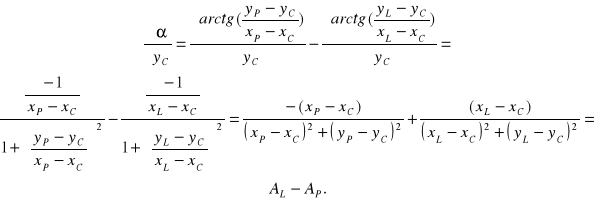
Współczynniki
,
,
,
itp.: są współczynnikami kierunkowymi lewego i prawego ramienia kąta.

Wyznaczyliśmy sześć pochodnych cząstkowych. Z pochodnych tych formujemy wektor pochodnych
i jak powyżej wyznaczamy wartość błędu średniego
.

.

Tak obliczony błąd wyrażony jest w radianach. Aby wyrazić go w innych jednostkach np. w sekundach trzeba wyrażenie to pomnożyć przez współczynnik przeliczeniowy

Jeśli błąd ma być wrażony w sekundach wówczas
itp.

1

(x_a,y_a)

(x_c,y_c)

(x_b,y_b)

A

B

C

a

c

b

C(x_C, y_C)

β

γ

α

x

y

L(x_L, y_L)

P(x_P, y_P)

---