Mateusz Komada III rok chemia informatyczna

ĆWICZENIE 40b

WYZNACZANIE RZĘDU REAKCJI METODĄ CAŁKOWĄ

CEL

Celem ćwiczenia jest wyznaczenie przy pomocy metody całkowej rzędu reakcji utleniania jonów Fe²⁺ jonami ClO₃^- w środowisku kawśnym.

Światło widzialne białe składa się z fal elektromagnetycznych o długościach ok. 380 nm - ok. 780 nm. Barwa ciała świadczy o tym, że przepuszcza ono lub absorbuje promieniowanie z zakresu widzialnego w sposób zróżnicowany, selektywny.

Obserwowane zabarwienie ciała jest dopełnieniem barwy promieniowania i odwrotnie.

Optyczną charakterystykę substancji stanowi jej krzywa absorbcji, czyli wykres pokazujący zależność absorbcji od długości fali.

Warunkiem absorbcji promieniowania przez daną substancję jest odpowiedniość energii padającego promieniowania i zmian energii możliwych do wywołania w cząsteczce danej substancji.

Prawa Bouguer'a - Lamberta i Beer'a stanowią podstawę spektrofotometrii absorbcyjnej.

Bouguer i Lambert wykazali, że między natężeniem światła przepuszczonego I₁ a grubością warstwy roztworu l istnieje następująca zależność:

I₁ = I₀ · e ^-kl

gdzie:

I₀ - oznacza natężenie światła padającego

k - współczynnik absorbcji

Po zamianie logarytmów naturalnych na dziesiętne mamy:

I₁ = I₀ · 10 ^-Kl

Wielkość K nazywa się współczynnikiem ekstynkcji.

Beer stwierdził w 1852 roku że współczynnik ekstynkcji roztworu jest proporcjonalny do stężenia substancji absorbującej światło:

K = K₁ · C

Po połączeniu obu praw otrzymujemy zależność wyrażającą prawo Bouguer'a - Lambert'a i Beer'a :

I₁ = I₀ · 10^-KCl

lub

= K· C · l = A

gdzie:

A - absorbancja.

Odstępstwa od prawa Lambert'a - Beer'a mogą być spowodowane albo zmianami chemicznymi zachodzącymi w miarę zmian stężenia albo warunkami pomiaru wykonanego za pomocą nie dość dokładnego przyrządu.

OPRACOWANIE WYNIKÓW

nr kolbki	c Fe^+3 [mol/dm^3] * 10^-5		0,001 M. Fe^+3 v[cm^3]	A
1	2		0,5	0,197
2	4		1	0,333
3	6		1,5	0,553
4	8		2	0,705
5	10		2,5	0,07
6	12	3		1,088
a = 9041,43 b = -0,0024

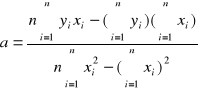
b =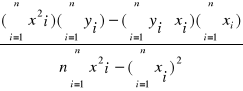

Niech c_Fe⁺³ będzie x a A będzie y, a n = 6.

0,00042
3,783
0,0003281
0,0000000364

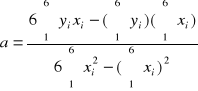
= 9041,43 b =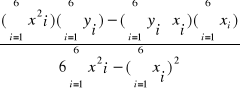
=-0,0024

Otrzymujemy zależność:

y = 9041,43x -0,0024

1)

6,12735*10^-6

8,78180*10^-6

1,19893*10^-5

1,53073*10^-5

1,86254*10^-5

2,21646*10^-5

2,53721*10^-5

2,89114*10^-5

3,25612*10^-5

3,63217*10^-5

3,98610*10^-5

4,37320*10^-5

4,70501*10^-5

5,14742*10^-5

5,53452*10^-5

5,93269*10^-5

6,33086*10^-5

6,72903*10^-5

7,14931*10^-5

7,54748*10^-5

7,95671*10^-5

8,36593*10^-5

8,77516*10^-5

9,19545*10^-5

9,61574*10^-5

0,000100360

0,000104563

0,000108766

0,000113079

400,9828

401,4100

401,9275

402,4643

403,0024

403,5781

404,1012

404,6799

405,2785

405,8971

406,4811

407,1217

407,6724

408,4090

409,0557

409,7230

410,3925

411,0642

411,7757

412,4519

413,1492

413,8489

414,5510

415,2745

416,0006

416,7292

417,4604

418,1941

418,9499

t [s]	A	cFe^+3 [mol/dm^3]	cFe^+2 [mol/dm^3]	1/c
60 120 180 240 300 360 420 480 540 600 660 720 780 840 900 960 1020 1080 1140 1200 1260 1320 1380 1440 1500 1560 1620 1680 1740	0,053 0,077 0,106 0,136 0,166 0,198 0,227 0,259 0,282 0,326 0,358 0,393 0,423 0,463 0,498 0,534 0,570 0,606 0,644 0,680 0,717 0,754 0,791 0,829 0,867 0,905 0,943 0,981 1,020		2,5*10^-3

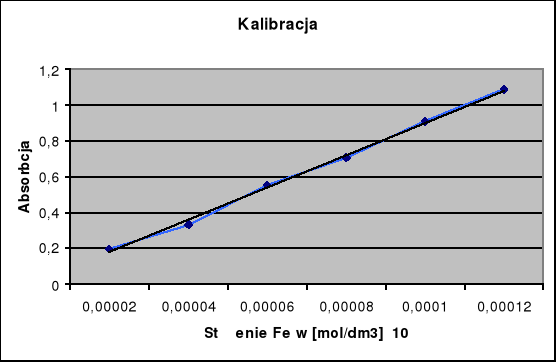
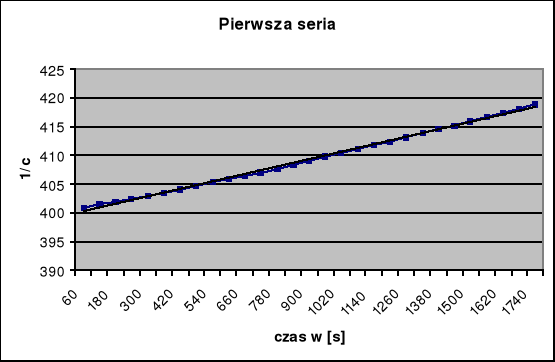
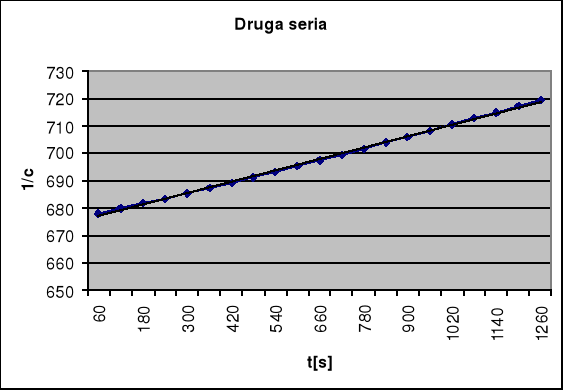
Aby znaleźć kolejne stężenia c_Fe⁺³ podstawiamy badane wartości do wzoru i wyliczamy. Następnie wykreślić musimy zależność 1/c od czasu. W tym celu liczymy wartość c z wzoru:

c = c₀ - c_Fe⁺³

gdzie:

c₀ - wartość początkowa stężenia jonów Fe⁺³

c - stężenie substratu po czasie t [s]

otrzymany wykres jest linią prostą spełniającą zależność:

Wartość k znajdujemy metodą najmniejszych kwadratów.

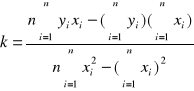
gdzie:

- y

t - x

26100
11871,63
10763414
30798000

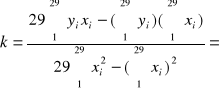
0,010803

Wartość współczynnika k wynosi 0,010803.

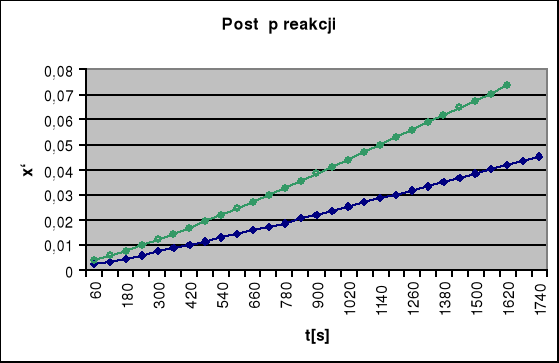
Aby wyznaczyć rząd reakcji kreślimy zależność postępu reakcji x` od czasu t[s]. Liczba postępu reakcji x` jest to stosunek stężenia przereagowanych jonów Fe ⁺² (x - w naszym przypadku jest ono równe stężeniu powstałych w wyniku reakcji jonów Fe⁺³) do stężenia początkowego substratu (c₀):

Stężenie przereagowanych jonów Fe⁺² jest równe stężenie powstałych jonów Fe⁺³, które możemy oznaczyć na podstawie krzywej kalibracyjnej.

Z wykresu x`= f(t) dla obu stężeń początkowych (wykresy umieszczone są na jednym układzie współrzędnych) odczytujemy wartość t₁ i t₂ dla dowolnej wartości liczby postępu reakcji i wstawiamy je do równania określającego rząd reakcji:

gdzie: c₀₁,c₀₂ - stężenie początkowe substratu dla 1 i 2 serii pomiarowej,

t₁, t₂ - czas dla danej liczby postępu reakcji dla serii pomiarowej 1 i 2.

2)

Dla drugiej serii pomiarowej przeprowadzam taką samą procedurę obliczeniową, korzystając z wykreślonej wcześniej krzywej kalibracji. Wyniki umieszczam w tabeli

6,37067*10^-6

9,02512*10^-6

1,16796*10^-5

1,49976*10^-5

1,83157*10^-5

2,17443*10^-5

2,52836*10^-5

2,90441*10^-5

3,30257*10^-5

3,67862*10^-5

4,07679*10^-5

4,48602*10^-5

4,89524*10^-5

5,31553*10^-5

5,74688*10^-5

6,17823*10^-5

6,60957*10^-5

7,04092*10^-5

7,47227*10^-5

7,91468*10^-5

8,35709*10^-5

8,79949*10^-5

9,2419*10^-5

9,69537*10^-5

0,000101267

0,000105691

0,000110226

669,5102

670,7021

671,8983

673,3996

674,9076

676,4730

678,0965

679,8300

681,6752

683,4271

685,2919

687,2192

689,1573

691,1592

693,2259

695,3050

697,3966

699,5009

701,6179

703,8025

706,0007

708,2128

710,4387

712,7348

714,9328

717,2013

719,5414

t [s]	A	cFe^+3 [mol/dm^3]	cFe^+2 [mol/dm^3]	1/c
60 120 180 240 300 360 420 480 540 600 660 720 780 840 900 960 1020 1080 1140 1200 1260 1320 1380 1440 1500 1560 1620	0,053 0,077 0,106 0,136 0,166 0,198 0,227 0,259 0,282 0,326 0,358 0,393 0,423 0,463 0,498 0,534 0,570 0,606 0,644 0,680 0,717 0,754 0,791 0,829 0,867 0,905 0,943		1,5*10^-3

Obliczam rząd reakcji n:

Dla dowolnie wybranego punktu wartości x`, np.: 0,02 otrzymujemy wartości czasów

t₁ = 827,88; t₂ = 496,73

możemy obliczyć rząd reakcji

n = 1 + log(t₁:t₂)/log(c₀₂:c₀₁)

n =1+ log(1,666)/log(0,6)

n =1+ 0,99991

n =1,99991
2

Reakcja jest niewątpliwie rzędu drugiego.

---