Funkcja wiodąca (skumulowana intensywność uszkodzeń)

Można ją interpretować jako miarę wyczerpywania się „zapasu

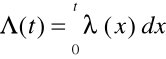
niezawodności obiektu”.

dla rozkładu wykładniczego:

dla rozkładu jednostajnego w przedziale od 0 do b:

Oczekiwany pozostały czas zdatności

jest to warunkowa wartość oczekiwana pozostałego czasu

zdatności
pod warunkiem, że w chwili t

obiekt jest zdatny.

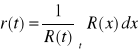
(charakterystyka funkcyjna zalezy od t)

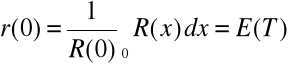
Możemy za pomocą oczekiwanego pozostałego czasu zdatności

r(t) wyrazić charakterystyki funkcyjne niezawodności:

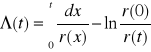
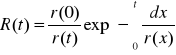
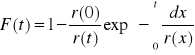
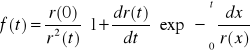
Dla odpowiednio dużych wartości argumentu t wartość funkcji r(t)

ulega niewielkim zmianom i dąży do:

Dla rozkładu wykładniczego:

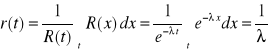
Dla rozkładu jednostajnego w przedziale od 0 do b:

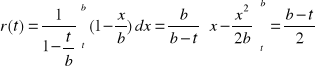
Podobnie możemy wyznaczyć oczekiwany czas zdatności obiektu

jeżeli wiadomo, że uszkodził się do chwili t:

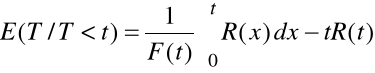
inaczej:

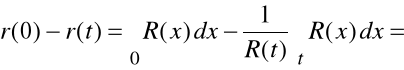
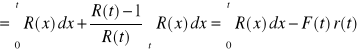
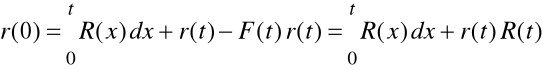
OBIEKTY NAPRAWIALNE:

Pi - prawdop.przebywania w dowolnej chwili t obiektu w stanie i

ZAŁOŻENIE UPRASCZAJĄCE

Po naprawie wraca do takiego samego stanu jak przed

uszkodzeniem

W t może wystąpić tylko jedno zdarzenie :

• Naprawa lub uszkodzenie

jeżeli:
;

,

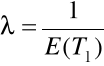
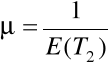
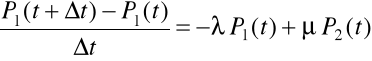
FUNKCJA GOTWOŚCI

Przebieh funkcji gotowości:

;

;

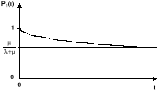
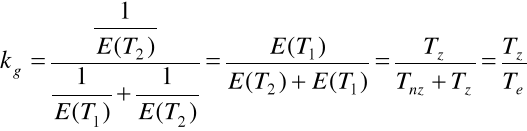
Tz- czas zdatności

Tnz- czas niezdatności

Te- czas eksploatacji

DWUSTANOWY PROCES EKSPLOATACJI

- całkowity czas eksploatacji

- całkowity czas użytkowania,

- całkowity czas obsługiwania,
=

i-liczba przejść obiektu do danego stanu

,

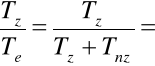
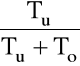
TRÓJSTANOWY PROCES EKSPLOATACJI

Tou- całkowity czas oczekiwania na użytkowanie

,

Too- całkowity czas oczekiwania na obsługiwanie

,

Przypadek 1

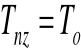
Wskaźnik gotowości technicznej:

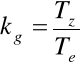
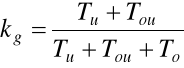
kw- wskaźnik wykorzystania obiektu zdatnego

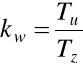
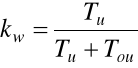
ke- wskaźnik efektywności obsługiwania obiektu niezdatnego

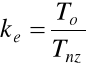
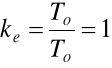
Przypadek 2

Wskaźnik gotowości technicznej:

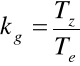
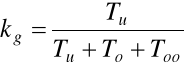
kw- wskaźnik wykorzystania obiektu zdatnego

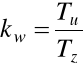
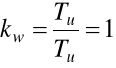
ke- wskaźnik efektywności obsługiwania obiektu niezdatnego

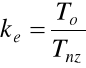
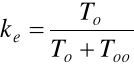
CZTEROSTANOWY MODEL PROCESU EKSPLOATACJI

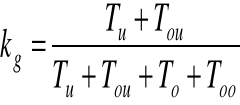
jeżeli: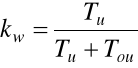

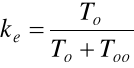
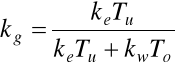
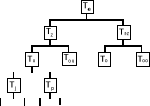
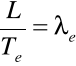
-intensywność eksploatacji

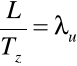
-intensywność użytkowania

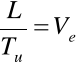
-prędkość eksploatacyjna

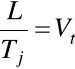
-prędkość techniczna

;

;

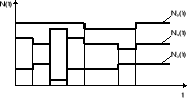
- liczba urządzeń użytkowanych w chwili t

- liczba urządzeń obsługiwanych w chwili t

Chwilowy wskaźnik gotowości technicznej:

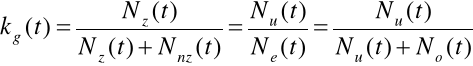
W przypadku jednorodnej grupy urządzeń eksploatowanych

w ustalonychwarunkach, można potraktować historię

eksploatacji grupy w krótkim przedziale jako ekwiwalentną

historii eksploatacji pojedynczego urządzenia tej grupy,

ale w dłuższym przedziale.

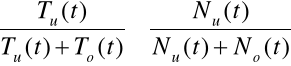
Niezawodność obiektów naprawialnych (odnawialnych)

Rozpatrzmy dwa przypadki:

1)czas naprawy (odnowy) jest bardzo mały w stosunku do czasu

życia elementu. Mówimy wówczas, że odnowa jest

natychmiastowa (czas jej trwania= 0)

2)czas naprawy (odnowy) posiada pewną skończoną

wartość i nie jest pomijalny.

ad. 1.

Chwile uszkodzeń (odnowień) obiektu są następujące:

...............................

......................................................

Chwile uszkodzeń (odnowień) przedstawiają

strumień losowy, który nazywamy strumieniem odnowy.

Zakładamy, że:

1) proces taki powtarza się nieograniczenie,

2) T1, T2,…są zmiennymi losowymi niezależnymi

o takim samym rozkładzie prawdopodobieństwa.

określonym dystrybuantą

,

i
dla wszystkich

są jednakowe i wynoszą:

,

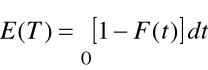
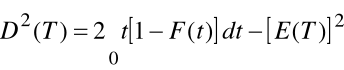
Niech N(t) będzie

zmienną losową określającą liczbę uszkodzeń (odnowień)

powstałych do chwili t. uogólniając

Zdarzenie
jest równoważne zdarzeniu

Dystrybuantę
można wyznaczyć dla dowolnego n:

PRAWDOPOD.WYSTAPIENIA DO CHWILI t

DOKLADNIE n USZKODZEŃ

P

zdarzenie
jest równoważne

zdarzenie
jest równoważne

Nie wystarczy wiedzieć jakie jest prawdopodobieństwo

wystąpienia n uszkodzeń (odnowień). Równie ważną informacją

jest oczekiwana liczba tych zdarzeń
.

Wielkość ta jest funkcją czasu określoną dla t > 0

oznaczaną
i nazywanąfunkcją odnowy (naprawy).

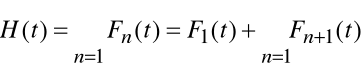
FUNKCJA ODNOWY- oczekiwana liczba uszkodzeń

( odnowień).Jest to funkcja czasu, określona dla t> 0

Równanie odnowy (odnowienia).

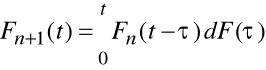
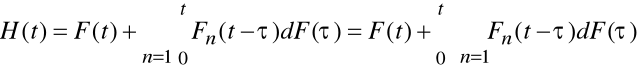
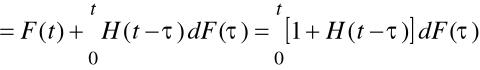
W praktyce często posługujemy się pochodna funkcji odnowy i nazywamy

ja gęstością odnowy.

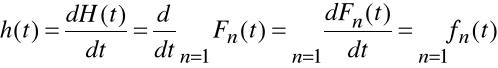
Funkcję H(t) wykorzystuje się do wyznaczenia oczekiwanej liczby

uszkodzeń w dowolnym przedziale czasu [t1,t2], wynosi ona

H(t2)-H(t1)

Przy pomocy H(t) można wyznaczyć

wariancję liczby uszkodzeń (odnów) w przedziale [0,t]

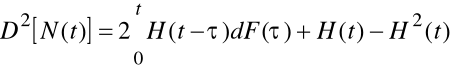
Badając proces odnowy przy

korzysta się z następujących twierdzeń:

Twierdzenie 1 (elementarne twierdzenie odnowy).

Jeżeli czas życia obiektu jest zmienną losową o dystrybuancie F(t)

i skończonej wartości oczekiwanej E(T), to

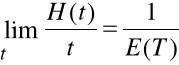
Oznacza to, że oczekiwana liczba odnowień w jednostce czasu

dąży do odwrotności średniego czasu życia obiektu, czyli średni

odstęp miedzy uszkodzeniami jest równy średniemu czasowi życia obiektu

Twierdzenie 2 (Blackwella)

Jeśli czas życia obiektu jest zmienną losowa typu ciągłego
o skończonej wartości oczekiwanej E(T) to dla > zachodzi:

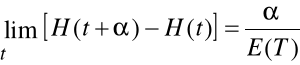
Oznacza to, ze po upływie długiego czasu liczba uszkodzeń w

przedziale o długości  zależy tylko od długości przedziału i

średniego czasu życia obiektu.

Twierdzenie 3 (Smitha)

Jeżeli czas życia obiektu jest zmienną

losową o skończonej wartości oczekiwanej E(T) oraz wariancji D²(T)

to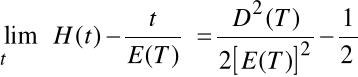

Proces odnowy o skończonym czasie odnowy (naprawy)

Ui-zmienne losowe wyrażające czas przebywania w stanie

niezdatności- czas naprawy

Zmienne T1,T2,…oraz U1,U2,… są zmiennymi losowymi

niezależnymi o rozkładach odpowiednio:

;

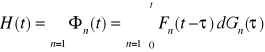
Po uszkodzeniu naprawa elementu

Zapobiegawczo można wymieniać elementy

Gdy intensywność uszkodzeń wzrosła do

Bardzo wysokiego poziomu

WYMIANA W USTALONYM WIEKU

;

gdzie:

- prawdopodobieństwo, że obiekt wymieniany
profilaktycznie w ustalonym czasie (co stały okres w)

nie uszkodzi się do chwili t,

- prawdopodobieństwo, że obiekt nie uszkodzi

się w kolejnych przedziałach czasu o długości w,

- prawdopodobieństwo, że obiekt nie uszkodzi się
w przedziale
;

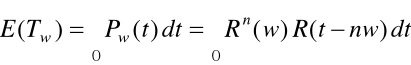
E(T_w) - oczekiwany czas do uszkodzenia obiektu;

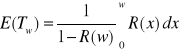
w-stały okres

DLA ROZKŁADU WYKŁADNICZEGO:

Naprawa nic nie zmienia, no zawsze będzie

DLA ROZKŁADU JEDNOSTAJNEGO:

Wartość w można wyznaczyć wg.rozmaitych kryteriów:

Np. - wg.kryterium ekonomicznego uwzględniając

-koszty wymian profilaktycznych

- koszty napraw wymuszonych uszkodzeniem obiektu

oraz charakterystyki niezawodnościowe obiektu

C(w) - jednostkowy koszt utrzymania obiektu; a - koszt

wymiany profilaktycznej; b - koszt naprawy wymuszonej

E(T_u) - oczekiwany czas użytkowania obiektu (do uszkodzenia

lub wymiany)

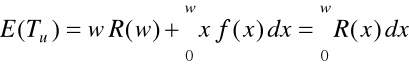
ODNOWA (NAPRAWA) NIEPEŁNA

Rozpatrzmy obiekt techniczny składający się z n elementów

składowych.

Załóżmy, że elementy są jednakowe w sensie ich niezawodności

Struktura niezawodnościowa obiektu jest szeregowa.

Funkcja niezawodności obiektu do chwili wykonania naprawy R1(x)

jest opisana zależnością

gdzie:
- funkcja niezawodności elementu

Jeżeli naprawa wykonana w chwili t polegała na wymianie k

spośród n elementów składowych to funkcja niezawodności

obiektu po naprawie R2(x) wynosi:

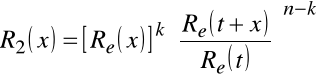
Z wzoru określającego R1(x) wynikają następujące zależności:

,

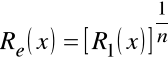
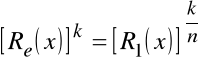
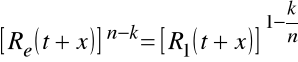
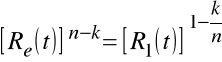
Po podstawieniu do zależności wyrażającej R2(x) otrzymujemy:

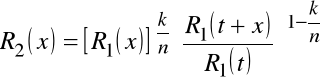
Jeżeli stosunek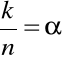
potraktujemy jako stopień

odnowienia obiektu (stopień naprawy), to:

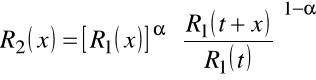
Logarytmując i następnie różniczkując stronami otrzymujemy:

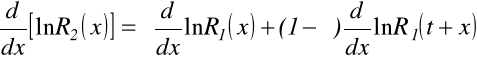
i podstawiając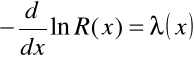
otrzymujemy

zależność wyrażająca związek między funkcjami

intensywności uszkodzeń
i
:

czyli

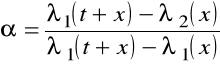
Można też współczynnik α przedstawić z

wykorzystaniem funkcji wiodących rozkładów

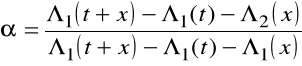
gdzie: