1.GRANICE FUNKCJI RZECZYWISTYCH JEDNEJ ZMIENNEJ.

Zakładamy, że funkcja
gdzie
jest określona dla x takich, że
to znaczy z ewentualnym wyłączeniem x₀. gdzie a>0

DEFINICJA:

Liczbę
nazywamy granicą funkcji f w punkcie x₀ jeżeli
piszemy wtedy

dla

WŁASNOŚCI FUNKCJI POSIADAJĄCYCH GRANICĘ

1. Funkcja f posiada w punkcie x₀ co najwyżej jedną granicę.

Dowód. Przypuśćmy, że
przy
, przy czym
. Ponieważ
, oraz
więc dla
takich, że
otrzymujemy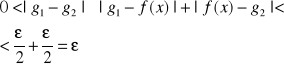

Co jest sprzeczne z założeniem g1 ≠ g2 , gdzyz wystarczy przyjąć 0<ε<Ig₁ -g₂I

czyli dla
otrzymujemy sprzeczność co kończy dowód.

2. Niech funkcja f będzie określona dla x takich, że
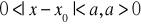
   . Na to, by funkcja f posiadała granicę g w punkcie x₀, potrzeba i wystarcza by dla każdego ciągu (x_n) takiego, że 0<|x₀-x_n|<a zbieżnego do x₀ ciąg wartości funkcji (f(x_n)) dążyłby do g.

Dowód

Konieczność zaklż€ f ma w x₀ granicę tzn.

Niech x_n będzie dolnym ciągiem zbieżnym do x₀ x_n≠x₀ dla n=1,2…

Oznacza to że:

Przyjmując ε'=δ otrzymujemy
dla n>N oraz

Zatem

Warunek dostateczny - DOSTATECZNOŚĆ

Przypuścmy, że dla każdego ciągu (x_n) zbierznego do x₀, n≠x₀ mamy
oraz funkcja f nie posiada granicy g w x₀> Oznacza to, że:

1)

obierzmy dowolny ciąg liczb dodatnich (δ_n) taki, że δ_n→0 przy

Oznaczamy przez ξ_n (ksi) punkt przedziału (x₀-δ_n, x₀+δ_n) różny od x₀ dla którego zachodzi (1)

Ponieważ
więc

Z drugiej stronydla każdego n=1,2… mamy na podstawie(1)
czyli ciąg (f(ξ_n)) nie dąży do g SPRZECZNOŚĆ.

c) Jeżeli funkcje f, g są określone w pewnym

otoczeniu punktu x₀ z ewentualnym wyłączeniem tego punktu oraz posiadają granice w x₀, to funkcje
posiadają granice w x₀, oraz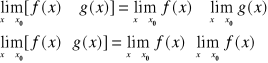

Jeżeli ponadto
! to iloraz
ma granicę w x₀ , oraz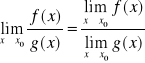

Dowód wynika z własności b.), oraz z odpowiednich tw. z teorii ciągów

3. Jeżeli funkcje f, g posiadają granice w punkcie x₀, oraz
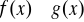
   dla x takich, że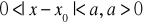
   to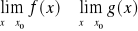
   

4. Twierdzenie o trzecich ciągach

Jeżeli funkcje f, g posiadają granicę g₀ € R w punkcie x₀, oraz funkcja h jest określona, spełnia warunek
w pewnym otoczeniu x₀, z ewentualnym wyłączeniem x₀, (z wyjątkiem co najwyżej x₀ to

Przykłady

1)

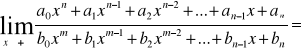
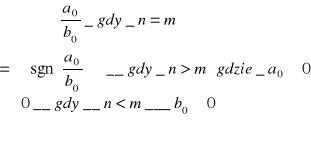
2) wykazać, że funkcja f9x)=sin(1/x) dla x≠0 nie posiada granicy przy x→0

DOWÓD:

Niech
dla n=1,2..

Widzać, że x_n→0. ponadto

=1*(-1)^n czyli f(x_n)nie posiada granicy, zatem nie istnieje (na mocy własności b))

DEFINICJA GRANIC JEDNOSTRONNYCH FUNKCJI

1.Niech funkcja f będzie określona dla x takich, że

0<x-x₀<a, gdzie a>0

Mówimy, ze funkcja f ma w x₀ granicę prawostronną, jeżeli istnieje taka liczba g_p, spełniająca warunek

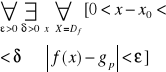
2.Niech funkcja f będzie określona dla x takich, że

o<x₀-x<a, gdzie a>0

Mówimy że funkcja f posiada w x₀ granicę lewostronną, jeżeli istnieje taka liczba g_l, że

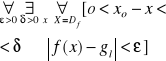
Granicę prawostronną oznaczamy symbolem

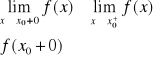
Granicę lewostronną oznaczamy symbolem

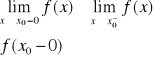
PRZYKŁAD;

Funkcja

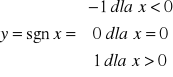
posiada w punkcie x₀=0 różne między sobą granice jednostronne:

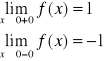
2)f(x)=[x] - część calowita x

Jeżeli x₀= c+
, gdzie c-l.czałkowita alfa- nieujemny ułamek właściwy 0≤alfa<1 to, [x₀]=c

Jeżeli x₀ jest liczbą całkowitą to f(x₀+0)=x₀ , f(x₀-0)=x₀-1. Jeżeli x₀ nie jest l. całkowitą to f(x₀+0)=f(x₀-1)

Twierdzenie 1

Niech funkcja f będzie określona dla x takich, że

0<x-x₀<a, a>0

Funkcja f posiada w x₀ granicę g wtedy i tylko wtedy, gdy posiada w x₀ granice jednostronne g_p , g_l oraz g_p=g_l=g.

Dowód. Konieczność.

Zakładamy, że w x₀ istnieje granica g funkcji f, tzn.

(1)

Z (1) wynika, że

(2)

czyli g=g_p oraz (3)

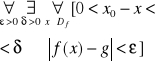
czyli g=g_l..

Zatem g=g_p a więc g_l=g_p=g

g=g_l

Dostateczność:

Zakładamy, że f posiada w x₀ równe sobie granice jednostronne: g_p=g_l=g.

Zatem zachodzą warunki (2) oraz (3). Zatem f posiada granicę g w x₀.

Zatem f(x)=sgn x nie posiada granicy w punkcie x₀.

(Posiada dwie równe sobie granice w x₀.)

Skończone granice jednostronne oraz skończoną granicę funkcji f w x₀ nazywamy granicami właściwymi.

W przypadku funkcji nieograniczonych w otoczeniu x₀ lub przy x→+∞(-∞) mogą występować tzw.: granice niewłaściwe funkcji.

DEFINICJA GRANIC NIEWŁAŚCIWYCH

Niech funkcja f będzie określona dla x takich, że

0<|x-x₀|<a a>0

Mówimy, że f posiada w x₀ granicę +∞ (-∞) jeżeli

Piszemy wtedy:

lub

Podobnie jak dla granic właściwych jednostronnych, można zdefiniować niewłaściwe granice jednostronne.

Np.

Niech funkcja f będzie określona na przedziale

X₀-a<x<x₀ , a>0

Mówimy, że f posiada w x₀ granicę lewostronną „-∞” jeżeli

Można również rozważać prawostronną granicę funkcji f dla x₀=-∞ którą oznaczamy symbolem

oraz lewostronną granicę funkcji f dla x₀=+∞ oznaczone przez
.

Granice te oznaczamy następująco

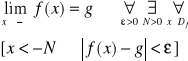
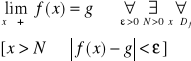
Określamy także granice:

Np.

Twierdzenie 2

a)Jeżeli

to

b)Jeżeli

to

c)Jeżeli

g(x)>0 w otoczeniu x₀ to

Twierdzenie 3 (o granicy superpozycji funkcji)

Niech funkcja f będzie określona dla y takich, że

0<|y-g₁|<a, a>0, a funkcja g dla x takich, że

0<|x-x₀|<b, b>0

Jeżeli

Przy czym funkcja g nie przyjmuje wartościg₁ dla
x 0<Ix-x₀I<0≤b to

Twierdzenie 4

Jeżeli f jest funkcją monotoniczną w pewnym otoczeniu x₀ to f posiada w x₀ obie granice jednostronne.

Twierdzenie 5 (Twierdzenie Bolzano-Cauchy`ego)

Niech funkcja f będzie określona dla x takich, że

0<|x-x₀|<a , a>0 (lub dla x>M>0)

Na to by funkcja f posiadała skończoną granicę przy x→x₀ (lub przy x→+∞) potrzeba i wystarcza, by spełniony był warunek (prz x→x₀)

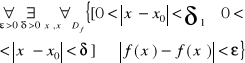
przy x do nieskończoności

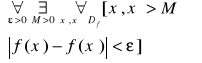
Można dowieść że:

gdzie a>0

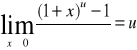
gdzie u€ R

3. CIĄGŁOŚĆ FUNKCJI RZECZYWISTYCH JEDNEJ ZMIENNEJ

DEFINICJA

Funkcję f określoną w pewnym otoczeniu punktu x₀ tzn. dla x takich, że |x-x₀|<a , a>0 nazywamy ciągłą w x₀, jeżeli istniejgranica skończona
.czyli

Gdzie g=f(x₀)

Przykłady funkcji ciągłych:

1) sin x , cos x, - funkcje ciągłe w każdym punkcie x₀∈R

2) f(x)=a^x, a>0 funkcja wykładnicza ciągła w każdym punkcie x₀∈R

3) f(x)=log_ax, a>0, a≠1 funkcja logarytmiczna ciągła w każdym punkcie x₀>0.

Funkcje nieciągłe w x₀ , ale określone w pewnym otoczeniu można sklasyfikować następująco:

1) Jeżeli istnieją skończone granice jednostronne

to funkcj f ma w x₀ nieciągłość I rodzaju.

Jeżeli ponadto istnieje skończona granica

To jest to nieciągłością I rodzaju usuwalną.

Można wtedy przez zmianę definicji funkcji f w x₀ uzyskać funkcje ciągłe w x₀.

Jeżeli natomiast granice jednostronne nie są równe, to f ma w x₀ nieciągłością I rodzaju nieusuwalną, a różnicą f(x₀+0)-f(x₀-0) nazywamy skokiem funkcji f w x₀.

2) Jeżeli funkcja najmniej ma w x₀ co najmniej jedna z granic jednostronnych w f posiada w nieciągłość II rodzaju.

Przykłady:

1)Funkcje ciągłe w każdym punkcie dziedziny: sinx, cos, tgx, ctg, a^x, log_ax

jest ciągła w

2)Funkcje nieciągłe

1)funkcja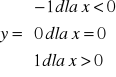
posiada w x₀ nieciągłość I rodzaju nieusuwalną, gdyż
.

Skok w punkcie nieciągłości jest równy 2f(0+0)-f(0-0)=2.

b) Funkcja Dirichleta

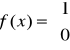
dla x€W- zbiór liczb wymiernych

dla x€R/W- zbiór liczb niewymiernych

Granice jednostronne funkcji f w każdym punkcie x€R nie istnieją, gdyż dowolnie blisko x₀ leżą liczby wymierne oraz niewymierne. Zatem f posiada w każdym punkcie x₀€R nieciągłość II stopnia

c) Niech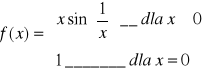

posiada w x₀=0 nieciągłość I rodzaju usuwalnego,
gdyż

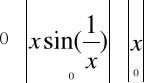
więc funkcja f ma w x₀=0 nieciągłość I rodzaju usuwalną

funkcja:

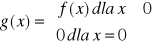
jest ciągła w x₀=0

Twierdzenie 1

Jeżeli funkcje f, g są ciągłe w punkcie x₀ , to funkcje
są też ciągłe w x₀. Jeżeli ponadto
, to
jest funkcją ciągłą w x₀.

Twierdzenie 2

Jeżeli w pewnym otoczeniu x₀ zachodzi nierówność
funkcje f, g są ciągłe w x₀ f(x₀)=g(x₀) to funkcja h jest ciągła w x₀.

Twierdzenie 3

Jeżeli funkcja g jest ciągła w x₀, a funkcja f jest ciągła w punkcie u₀=g(x₀) to funkcja złożona
jest ciągła w x₀.

DEFINICJA

Niech funkcja f będzie określona dla x takich, że w pewnym prawostronnym otoczeniu punktu x₀ ≤x<x₀+a ) , a>0. mówimy, że f jest prawostronnie ciągła w x₀ , jeżeli istnieje skończona granica
. oraz

Analogicznie określamy lewostronną ciągłość funkcji f w punkcie x₀.

Def:

Funkcja f(a,b) →R jest ciągła na (a,b), jeżeli f jest ciągła w każdym punkcie x₀€(a,b).

Def:

Funkcję
nazywamy ciągłą na przedziale domkniętym <a,b> jeżeli f jest ciągła na przedziale otwartym (a,b), prawostronnie ciągła w x₁=a oraz lewostronnie ciągła w x₂=b.

CIĄGŁOŚĆ JEDNOSTAJNE

Mówimy, że funkcja f:X→R, gdzie X jest przedziałem otwartym lub domkniętym osi rzeczywistej, jest jednostajnie ciągła na przedziale X jeżeli
Widać, że każda funkcja jednostajnie ciągła na X jest cięgła w każdym punkcie x₀€X. Twierdzenie odwrotne nie zachodzi

Przykłady:

1) Dowieśc, że funkcja F(x)=x+sinx , x€R jest jednostajnie ciągła na R

Dowód: Obieramy dowolnie x',x''€R wtedy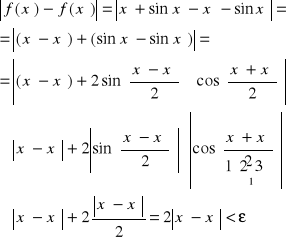
Skorzystamy z oszacowania IsinuI≤IuI dla u€R

Zatem dla x',x;;€R takich, że Ix'-x''I<ε/2 Otrzymujemy

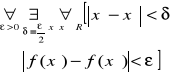
2)wykazać, że funkcja f(x)=1/x dla x€(0,a>, a>0 jest ciągła na przedziale (0,a> oraz f nie jest ciągła na tym przedziale

Dowód:

Dla każdego x₀€(0,a>

Wykażemy, że:

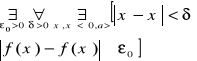
Niech ε₀=1 Dla dowolnego oznaczamy x'=1/n, x''=1/(n+1), gdzie n€N jest tak, że x', x;''€(0,a>. Wtedy

dla odpowiednie dużego
oraz

czyli f nie jest ciągła jednostajnie W x_o=0 f posiada nieciągłość II rodzaju. W przedziale półdomkniętym (0,a> , a>0 f jest ciągła, ale nie jest ciągła jednostajnie.

WŁASNOŚCI FUNKCJI CIĄGŁYCH NA PRZEDZIALE DOMKNIĘTYM

Zakładamy, że funkcja f
jest ciągła na przedziale domkniętym <a,b>. Wtedy:

1)Funkcja f jest ograniczona na <a,b>tzn

2)Funkcja f jest jednostajnie ciągła na <a,b>, tzn.

3)Jeżeli
, to istnieje taki punkt

f(c)=0

4)Funkcja f osiąga w <a,b> swoje kresy, tzn. istnieją takie punkty
, że

5)WŁASNOŚĆ DARBOUX

Funkcja f przyjmuje w przedziale <a,b> wszystkie wartości zawarte między jej kresem dolnym i kresem górnym, tzn. wartości funkcji f wypełniają przedział domknięty

6)Jeżeli jest ściśle monotoniczna tzn. rosnąca lubmalejąca na <a,b> to funkcja odwrotna f-1 jest ciągła na przedziale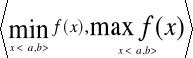
VI RACHUNEK RÓŻNICZKOWY FUNKCJI RZECZYWISTYCH

1.POCHODNA FUNKCJI RZECZYWISTEJ ZMIENNEJ RZECZYWISTEJ

Dana jest funkcja

Niech x₀∈(a,b). Przyrostem zmiennej niezależnej w x₀ nazywamy różnicę
a przyrostem zmiennej zależnej w x₀ nazywamy różnicę
.

Iloraz różnicowy
.

przy
to tzw. Iloraz różnicowy f w x₀. Jeżeli przy
istnieje granica właściwa lub niewłaściwa ilorazu różnicowego
funkcji f w x₀, to punktowi x₀ można przyporządkować wyrażenie

.

Zmieniając x₀∈(a,b) otrzymujemy funkcję f ,, gdzie

DEFINICJA POCHODNEJ

Funkcję
, gdzie

nazywamy pochodną funkcji f.

DEFINICJA

Funkcję f', gdzie
nazywamy pochodną funkcji f

DEF: Pochodną lewostronną funkcji f nazywamy funkcję
gdzie
.

Pochodną prawostronną funkcji f nazywamy funkcję
gdzie
.

PRZYKŁAD:

Korzystając ze wzoru (1) oraz ze wzoru (2) i(3) zbadać pochodną funkcji ciągłej f(x)=IxI, dla x∈R w punkcie x₀=0

ROZWIĄZANIE:

Funkcja f jest jednostajnie ciągła na R.

Pochodne jednostronne funkcji f w x₀=0 wynoszą:

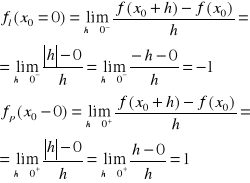
Ponieważ
, więc nie istnieje pochodnaf'(0) mimo, że funkcja f jest ciągła w x₀

Poza x₀€pochodna funkcji f istnieje i wynosi: dla x₀>0

f'(x₀)=-1 gdy x₀<0

Twierdzenie 1 Skończona pochodna - ciągłość

Jeżeli funkcja f określona na przedziale (a,b) ,ma skończoną pochodną w x₀€(a,b) to f jest ciągła w x₀.

DOWÓD:

Ponieważ istnieje f'(x0)€R

Więc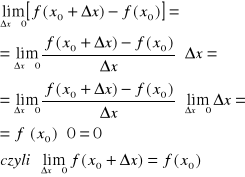

Zatem f jest ciągła w x₀.

Twierdzenie odwrotne nie jest zachodzi (patrz przykł wyżej).

Twierdzenie 2

Jeżeli funkcje f,g posiadają skończone pochodne w punkcie x₀, to:

a) kombinacja liniowa αf+βg, gdzie α,β€R, posiada skończoną pochodną w x₀ oraz

B)iloczyn f⋅g posiada skończoną pochodną w x₀ oraz

DOWÓD

Obliczamy pochodną funkcji y=f(x)⋅g(x) w punkcie x₀ .

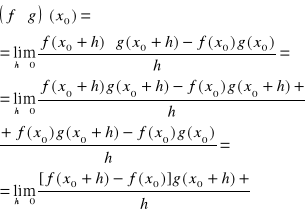
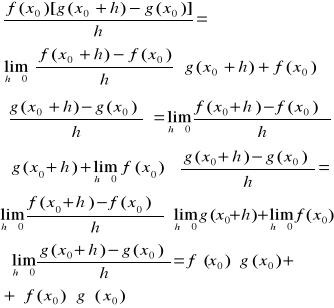
f(x₀) jest liczbą stałą niezależną od h więc
oraz z definicji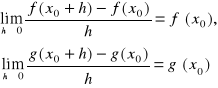

Zatem
gdyż g jest ciagła w x0

C)jeżeli g(x₀)≠0 oraz ponieważ g jest ciągła w x0(bo istnieje g(x0)€R więc dla dostatecznie małych ∆x g(x₀+∆x)≠0 stąd:

DOWÓD

Obliczamy pochodną fun.
w punkcie x₀

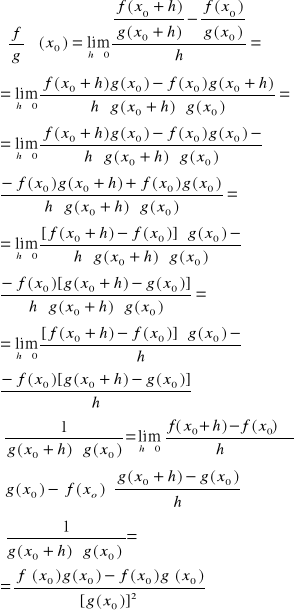
Ponieważ

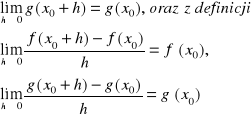
zatem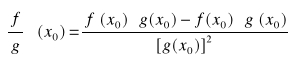
g(x₀)≠0

Twierdzenie 3

Jeżeli:

A) funkcja g jest określona na <a,b> oraz istnieje skończona pochodna
dla pewnego x₀∈(a,b)

B) funkcja f jest określona na przedziale <c,d>⊃<a,b>-przeciwdziedzina funkcji g,f, funkcja f ma skończoną pochodną w punkcie g(x₀), to:

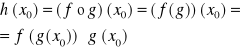
Twierdzenie 4

Jeżeli funkcja f jest ściśle monotoniczna na <a,b> oraz istnieje skończona pochodna
w punkcie x∈(a,b), to funkcja odwrotna
do funkcji f posiada pochodną w punkcie y₀=f(x₀) oraz

POCHODNA FUNKCJI ELEMENTARNYCH

c-stała	0
sin x	cos x
cos x	-sin x
tg x
ctg x
arc sin x
arc cos x
arc tg x
arc ctg x
sin h x	cos h x
cos h x	sin h x
tgh h x
ctg h x

3

Barbórka & Natala

---