Bardzo krótko opracowane tezy na filozofie przyrody. Sama ta treść nie gwarantuje posiadania wystarczającej wiedzy, ale choć trochę przybliży zagadnienia .

(puste pola wymagają rysunku odręcznego-brak czasu, aby cudować na kompie)

1. PROBLEMATYKA PRZESTRZENI

a) typologizacja doświadczenia przestrzeni: psychologiczne, fenomenologiczne, opis ilościowy

Psychologiczne - próba zbadania naszego doświadczenia przestrzenności, w perspektywie zmysłów; poznanie przestrzeni związane jest z naszymi zmysłami. Nasze doświadczenie przestrzenności zależy od naszych zmysłów (jest przestrzeń wzrokowa, dotykowa, motoryczna, wyobrażeniowa).Osoba niewidoma posiada przestrzeń tylko dotykową.

Fenomenologiczne - to taki rodzaj doświadczenia, który nie tylko zależy od naszych zmysłów i zawiera te psychologiczne doświadczenia, ale wiąże je z pewnymi sensami. Człowiek będzie to doświadczenie przestrzenności wiązał ze znaczeniami np. uczucie swoistości i obcości; czy też dostrzeganie pewnych jakości przestrzenności to doświadczenie fenomenologiczne jest w pewnym sensie centralne, oprócz opisów jakościowych, jest też opis ilościowy (obok terminów fenomenologicznych dodajemy opis ilościowy np. równoległość, prostopadłość, długość - to dodaje właściwości przestrzenności).

Opis ilościowy

W obrębie doświadczenia przestrzenności pojawia się możliwość ilościowego potraktowania (daleko, blisko). Widać tu dobrze, że pewne elementy doświadczenia przestrzenności dadzą się ilościowo opisać, a pewne nie. Jak opisać ilościowo przytulność, swojskość? Nie można. A jak opisać ilościowo ile pola mi się należy, jak mam drugiego brata, a ojciec dał 2 hektary do równego podziału pomiędzy nas dwojga? Łatwo można to podzielić. Zatem pole mogę zmierzyć, objętość mogę zmierzyć, odległość mogę zmierzyć. Ruch, który się odbywa w przestrzeni też mogę opisać. Ale różne doświadczenie psychologiczne (ślepy, widomy) nie za bardzo się poddaje opisowi. Doświadczenie fenomenologiczne też nie za bardzo się poddaje opisowi.

Własności przestrzeni zakładane w ilościowym opisie; przestrzeń jest:

1) homogeniczna - jednorodna - w każdym miejscu taka sama

2) izotropowa - taka sama w każdym kierunku (jak idziemy jedną drogą, to przestrzeń, która nas otacza się nie zmienia, gdy idziemy w różnych kierunkach, to przestrzeń dalej zostaje taka sama

3) ciągła - nasze doświadczenie przestrzeni, doświadczenie czasu, które bierze się z naszego potocznego doświadczenia, doświadczenie ciągłości, przestrzeń jest ciągła.

b) matematyczne modele przestrzeni: metryczny, liniowy, Euklidesowy, Riemannowski

Przestrzeń metryczna - zbiór punktów nieskończonych x={x,y,z,…}, w których zadana jest funkcja przyporządkowująca każdej parze punktów nieujemną liczbę i spełniająca następujące własności:

d (x,x) = 0 gdzie: d - odległość, metryka

d (x,y) = d (y,x)

d (x,y) ≤ d (x,z) + d (y,z)

Oto następujące własności odległości (3 elementarne własności):

- Odległość jakiegoś punktu od siebie samego równa się 0.

- Odległość między punktem A i B jest taka sama jak między punktem B i A.

- Jeśli mamy jakieś 3 punkty (A,B,C), to odległość między punktami A i B jest mniejsza, lub równa sumie odległości punktów A i C oraz B i C.

(* to akurat do tego zagadnienia jako modelu matematycznego nie musi być, ale pozwoli trochę rozjaśnić )

W tej przestrzeni mamy do czynienia tylko z odległościami. Odległość między dwoma punktami w przestrzeni to pewna liczba, długość tego odcinka, liczba, którą temu odstępowi między A a B przyporządkowujemy, mamy miarę i mierzymy w jakiś tam jednostkach, ileś tam ta liczba wynosi.

Przestrzeń liniowa - przestrzenią liniową L, L=(l₁,l₂,l₃) nad ciałem K, nazywamy zbiór L z dwoma wyróżnionymi działaniami wewnętrznymi:

1. Dodawanie
   

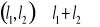
Każdej parze z tego zbioru będzie przyporządkowywać nowy element (l₁+l₂). Tego + nie można kojarzyć jako dodawania liczb do siebie (np. 3+2). To nie jest taki rodzaj dodawania, tylko jest to pewna operacja w tym abstrakcyjnym zbiorze, który składa się z jakichś elementów. Gdy dwa element ze sobą połączymy, to dostaniemy trzeci, który też będzie należał do tego zbioru.

2. 
   

Takiej parze przyporządkowujemy taki element, który oznaczony jest symbolem al, czyli mnożenie.

Zakładamy przy tym, że spełnione są następujące aksjomaty:

1. Dla każdego
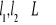
   to złożenie (które nazwaliśmy dodawaniem), też należy do tego zbioru, czyli: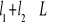
   

2. Przemienność operacji dodawania
   

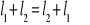
3. Spełniona jest tzw. łączność:
   
   

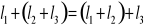
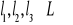
Ten aksjomat opowiada o tym, co robić, gdy mamy tych złożeń wiele, że nie tylko 2, ale np. 3 złożenia pod rząd. Mówi to nam, że wynik nie zależy od kolejności składania. Jeżeli najpierw dodam element l₂ i l₃ a dopiero do niego dodam l₁, to wyjdzie tyle samo, jakbym najpierw złożył l₁ z l₂ a potem to co mi wyjdzie z tego, co oznacza ten nawias, złożę z tym elementem l₃.

4. Istnieje element 0 nazywany elementem zerowym, taki, że dla każdego
   

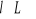
5. Dla każdego elementu
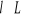
   istnieje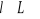
   , taki, że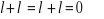
   

Ten element l', który zwykle jest oznaczany -l, nazywamy elementem odwrotnym do elementu l.

6. Dla każdego
   
   

7. 
   ,
   
   

,

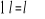
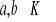
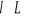
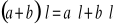
Euklidesowy model przestrzeni - Trójwymiarowa przestrzeń Euklidesa jest przestrzenią liniową, metryczną, przestrzenią wektorową. Metryka jest zadawana przez iloczyn skalarny. Jest to najprostszy model przestrzeni, w której nie ma krzywizny.

Bierzemy przestrzeń L, która jest przestrzenią liniową, i w tej przestrzeni określamy iloczyn skalarny - taka wielkość, która dowolnym dwóm elementom x,y należącym do tej przestrzeni liniowej, będzie przyporządkowywać liczbę rzeczywistą:

< | > = iloczyn

i będzie posiadać następujące własności:

1. 
   

2. 
   

3. 
   

Jest to znowu abstrakcyjna definicja jakiejś operacji dodatkowej, którą wprowadzamy w przestrzeni liniowej.

<* tworzymy matematyczny model>

Zobaczmy teraz jak ta operacja wygląda na tych przykładach, które żeśmy tutaj wywołali.

To co jest tutaj ważne to to, że ten iloczyn skalarny określa długość w tej przestrzeni.

Zadaje on metrykę w przestrzeni i za jego pomocą możemy określić odległość między dwoma wektorami.

W ten sposób zyskujemy ten potrzebny nam model, za pomocą którego określa się tą trójwymiarową przestrzeń, w której żyjemy. Strukturą matematyczną, która nam będzie dobrze modelować przestrzeń w której żyjemy, jest taka przestrzeń Euklidesowa.

Riemannowski model przestrzeni - zakłada się, że to jest przestrzeń, której krzywiznę potrafimy podać za pomocą matematycznych formuł; i ma ona taką właściwość, że lokalnie na małych odległościach jest przestrzenią Euklidesową. (Jest to jakaś przestrzeń skrzywiona i na małych odległościach daje się dobrze modelować przez przestrzeń Euklidesową).

c) ontologia przestrzeni: spór Leibniza i Clarka, ogólna teoria względności a natura przestrzeni

Ten świat, który Leibniz opisuje za pomocą swoich pojęć filozoficznych, jest światem, w którym rządzi się zasadą sprzeczności (nie ma sprzeczności), to co pojawia się jako sprzeczne to trzeba odrzucić. Druga zasada, która rządzi tym światem Leibniza to jest zasada racji dostatecznej. Formułował ją w taki sposób: „Żaden fakt nie może się okazać rzeczywistym, czyli istniejącym, żadna wypowiedź prawdziwą, jeżeli nie ma racji dostatecznej, dla której ten fakt czy ta wypowiedź są takie a nie inne.”

CLARK	LEIBNIZ
Teza Newtona: istnieje absolutny czas i absolutna przestrzeń jako obiekty faktyczne absolutny czas i absolutna przestrzeń są zmysłami Boga Bóg realizuje Swoją wszechobecność w świecie poprzez to, że to są Jego zmysły	Od strony przeświadczeń teodycalnych uważa, że religia naturalna bardzo słabnie, bo np. jeden uważa dusze za cielesną a drugi uważa samego Boga za cielesnego
Narzędzie, które Bóg używa, aby poznawać rzeczy. Po obliczeniu przez Newtona stabilności układu wyszło mu, że on się kiedyś rozleci, tu potrzebna jest ingerencja Boga	Wg Leibniza światem rządzą dwie zasady: - zasadą sprzeczności - prawda i fałsz nie istnieją równocześnie, - zasada racji dostatecznej - żaden fakt nie może się okazać rzeczywistym bez racji zaistnienia, wszystko żeby istnieć musi mieć racje dostateczne.
Przestrzeń i czas są ilościami. Położenie zaś i porządek nimi nie są. Przestrzeń z natury ma taka własność, że jest zmetryzowana, daje się określić odległościami między punktami. Tą miarą właśnie jest metryka.	Świat składa się z niepodzielnych substancji dobrze uporządkowanych zwanych monadami. Musi być powód istnienia czasu i przestrzeni. Należy postawić pytanie jak trzeba myśleć o czasie i przestrzeni by zadziałała racja dostateczna. W przestrzeni istnieją relacje pomiędzy punktami i one są właśnie tą racją dostateczną. Ta owa relacyjna koncepcja mówi, że położenie każdego punktu jest wyznaczone przez relacje tego punktu jest z pozostałymi punktami. Dany punkt jest tam bo inne punkty określają położenie tego punktu.
Istnieje jakaś substancjalna przestrzeń absolutna.	Konsekwencją relacji Leibniza jest to, że konfiguracja ciał jest tożsama z przestrzenią. Racja dostateczna = relacje porządkujące zbiór punktów w przestrzeni.
	Przestrzeń nie jest niczym innym jak porządkiem rzeczy.

Głównym pytanie całego sporu brzmi: Jaka jest natura rzeczy? Czy istnieje ona niezależnie od rzeczy - Newton lub czy jest ona wyznaczona przez rzeczy - Leibniz?

ogólna teoria względności - Według niej materia (rozkład mas i energii w przestrzeni) zmienia charakter przestrzeni. Materia jako przejaw energii wpływa na krzywiznę przestrzeni. Z jednej strony obiekt opisuje materię z drugiej obiekt opisuje krzywiznę. Związek dający się uchwycić pomiędzy materią a krzywizną to przestrzeń.

d) epistemologia przestrzeni - koncepcja I. Kanta

Kant zadał pytanie, którego nikt nie postawił: „Czy przestrzeń to coś rzeczywiście istniejącego?

Odpowiedź Kanta: „Przestrzeń jest koniecznym wyobrażeniem a priori, leżącym u podłoża wszelkich zewnętrznych danych naocznych.”

Za przestrzenność Kant uważa to, co ja mam w głowie. Kant odchodzi od ontycznego myślenia, którym zajmowali się Newton z Leibnizem. Najważniejsze dla Kanta jest to jak zrozumieć nowożytne przyrodoznawstwo, czyli matematykę. Gdyż ja uważa za narzędzie do pomocy w poznawaniu świata przyrody.

Podział typów sądów u Kanta:

- analityczne - niczego nie dodają do treści poznania tego, o czym ten sąd jest orzekany np. wszystkie ciała są rozciągłe

- syntetyczne - poszerza sąd, zawiera w treści to, czego nie ma w samym pojęciu np. niektóre ciała są ciężkie.

Podział sądów ze względu na stosunek do doświadczenia:

- a priori - wypływają z czystego intelektu, są niezależne od wszelkich wrażeń zmysłowych

- a posteriori - takie, w których mamy nową treść empiryczną, którą zdobyliśmy z naszego kontaktu ze światem

Kant zastanawia się czy możliwe jest zdobycie nowej wiedzy bez odwoływania się do empirii. Czyli czy możliwe są sądy syntetyczne a priori. Czyli jak ja będę po prostu myślał bez kontaktu z empirią, to czy dostanę jakaś nową wiedzę? Uważa, że takie sądy są w matematyce np. 2+2=4 jest nową wiedzą, która zdobyliśmy.

Czysta naoczność- to co wprowadza na do sądów a priori wcześniej od naszych zmysłów. Przestrzeń jest jedną z tych form czystych naoczności, która nie jest w świecie, ale jest czymś co bierze się ze świata. Wyobrażenie przestrzeni nie może być zapożyczone przez doświadczenie ze stosunków występujących jakiś mechaniczny sposób.

Przestrzeń- jest koniecznym wyobrażeniem a priori leżącym u podłożą wszelkich zewnętrznych danych naoczności.

2. PROBLEMATYKA CZASU

a) Ludzkie doświadczenie czasu, przemijania.

Upływ czasu wygląda różnie (komuś coś się może dłużyć, a inny się nawet nie zreflektuje, że już tyle czasu upłynęło) ale generalnie możemy o nim mówić. Każdy ma jakieś doświadczenie tego upływu. Upływ czasu idzie w jedną stronę, idzie do przodu, nie da się tego cofnąć. Możemy różnie się odnosić do tego doświadczenia czasu. Gdybyśmy byli istotami, w których świecie nie ma zmian, pór dnia, to byśmy nie wpadli na to czym jest czas. Czas biegnie w sposób kolisty.

b) ilościowy model- prosta rzeczywista i jego adekwatność

Jako, że czas jest tematem myśli musimy uzmysłowić sobie pewne poczucie ciągłości oraz pewne elementy miary. Ten nasz model czasu, który jest osią wszystkich liczb rzeczywistych posiada trzy właściwości:

• nierówność (później- wcześniej), która wyraża porządek na tej osi liczb rzeczywistych

• odległość między dwoma punktami. Musi to być koniecznie zbiór liczb rzeczywistych, bo gdybyśmy wzięli zbiór liczb naturalnych to między liczbami 1 a 2 powstała by luka, podobnie w zbiorze licz wymiernych, bo pomiędzy ¾ a 4/4 istnieje pewna luka. Dlatego musimy dodać do zbioru liczb wymiernych zbior licz niewymiernych, które wspólnie z wymiernymi dadzą nam zbiór liczb rzeczywistych

• zachowana jest ciągłość- oddaje jednostajny upływ czasu

c) Czasoprzestrzeń Minkowskiego: niezmienniczość interwału czasoprzestrzennego, problem równoczesności, diagramy czasoprzestrzenne, paradoks bliźniąt, stożki świetlne, zachowanie struktury chronologicznej i przyczynowej, czas wszechświata.

Model czasoprzestrzeni Minkowskiego związany jest ze szczególną teorią względności. Nie można tu mówić ani o absolutnym czasie, ani o absolutnej przestrzeni, ponieważ prędkość światła jest taka sama w różnych układach odniesienia, zdarzenia będą równoczesne, ale tylko w tym samym układzie odniesienia. W odwzorowaniu geometrycznym szczególnego znaczenia nabiera obraz stożka świetlnego wyznaczonego poprzez linie światła.

Odległość między zdarzeniami (t,x),(t',x')ma charakter absolutności. Ona nie zależy od układu odniesienia. Czas i położenie to współrzędne jednego punktu, które mają bardzo podobne właściwości.

Przy prędkościach zbliżonych do prędkości światła terminy te się mieszają (ujawnia się efekt relatywistyczny)

Interwał czasoprzestrzenny

Interwał czasoprzestrzenny ma charakter niezmienniczości. Jest to wielkość, która nie zależy od układu odniesienia (inercjalnego układu odniesienia)

Ruch jednostajny z prędkością V.

Zdarzenie - zajście takiej sytuacji, gdzie

opisujemy i czas i przestrzeń razem

Miarą nachylenia tych prostych jest prędkość obiektu.

Interwał czasoprzestrzenny może mieć różne znaki:

s²(p) = (ct)² - x² -y² - z²

(ct)² - x² = 0 - są to odległości, które leżą na stożku świetlnym

Odległości większe od zera leżą wewnątrz stożka i będą miały charakter czasoprzestrzenny.

Odległości mniejsze od zera leżą na zewnątrz stożka i mają charakter przestrzenno podobny.

Jeśli zmienię układ odniesienia to kierunek upływu czasu może się zmienić.

We wnętrzu stożków świetlnych istnieje uporządkowanie czasowe, które ma charakter absolutny, nie ma chaosu.

Przyszłość zdarzenia p składa się z tych wszystkich punktów do których można dotrzeć startując z p z prędkością nie przekraczającą prędkości światła. Podział na przyszłość i przeszłość jest podziałem nie zależnym od układu odniesienia. Przyszłość i przeszłość nie mieszają się ze sobą.

Diagramy czasoprzestrzenne

Możemy próbować rozrysowywać sobie rozmaite sytuacje, gdzie bierzemy oś czasu i jeden z wymiarów przestrzennych.

Jak zatem te diagramy czasoprzestrzenne będą wyglądać?

Zdarzenie polega na tym, że gdzieś siedzę, nie poruszam się, tylko płynie czas. Moje zmienne przestrzenne zatem nie ulegają zmianie, a czas płynie. Widać, że diagramem czasoprzestrzennym każdej z siedzących tutaj osób będzie prosta równoległa do osi czasu.

Ciągle jest to samo położenie, ale czas się zmienia. Każdej późniejszej chwili odpowiada tutaj kolejny punkt tej prostej. Jest to taki najprostszy diagram czasoprzestrzenny obiektu, który się nie porusza, a czas płynie.

Inna sytuacja: obiekt porusza się ruchem jednostajnym prostoliniowym.

W takiej sytuacji ruchowi prostoliniowemu o stałej prędkości, będzie odpowiadać prosta. Nachylenie tej prostej jest związane z wielkością prędkości. Im prędkość jest większa, tym nachylenie tego diagramu będzie się zmieniać.

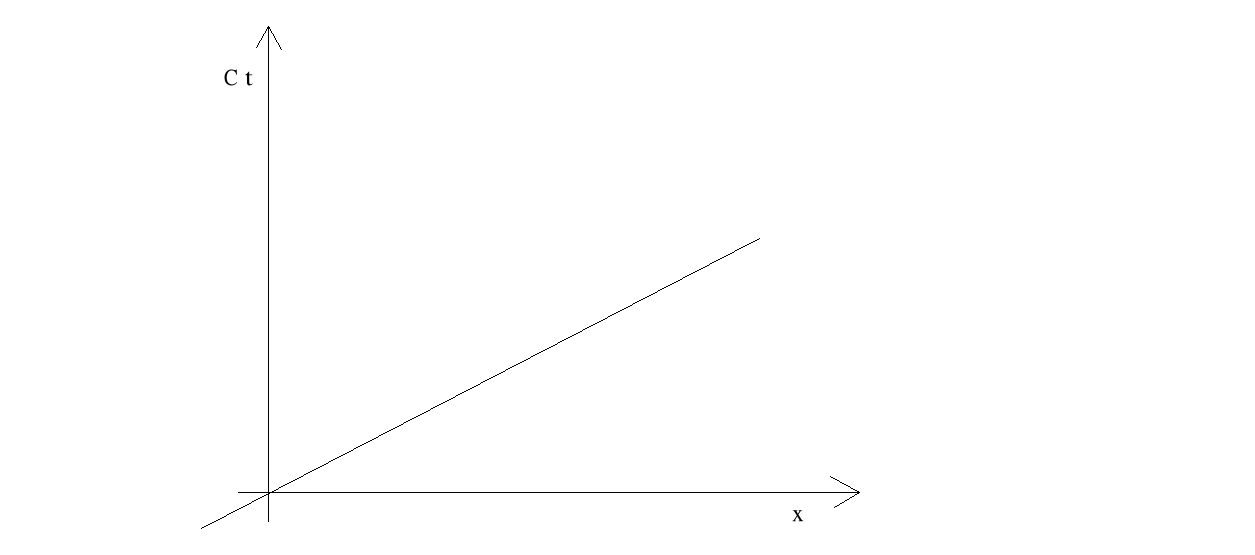
Paradoks bliźniąt - polega on na tym, że mamy dwoje bliźniaków i jedno z nich pozostanie w domu, a drugie wsiądzie do rakiety. Gdy ten drugi, który był w rakiecie (poruszającej się z prędkością zbliżoną do prędkości światła) powróci do domu zastanie swojego brata bliźniaka jako dziadka mim, że urodzili się w tym samym czasie.

Dylatacja czasu - upływ czasu zależy od prędkości.

d) Zasada wzrostu entropii, a nieodwracalność upływu czasu.

Pojęcie entropii, które pojawia się w połowie XIX w., wprowadza je Rudol Clausius, to jest takie pojęcie, które ma opisywać miarę nieodwracalności, tego, że część energii cieplnej pozostaje niezamieniona na pracę. Jak mamy taką sytuację, w której jest układ izolowany, w którym jakieś procesy przebiegają, nie ma żadnych wymian energii z otoczeniem, energia jest wówczas zachowana w tym układzie izolowanym, natomiast ta entropia jako miara takiego niepełnego przekształcania się energii cieplnej na jakiekolwiek inne formy energii, ta wielkość będzie rosła, zawsze zwiększała swoją wartość, bądź będzie się nie zmieniała, gdy jest już taka maksymalna degradacja, że ta wartość entropii osiąga maksimum, nie ma żadnych innych form energii jak energia cieplna i nie ma żadnych innych procesów, które by przeprowadzały tą energię cieplną w jakąkolwiek inną postać energii. Ta II zasada termodynamiki jest różnie formułowana. Albo w taki sposób jak była tu mowa o tych silnikach, albo używając pojęcia entropii, że entropia w tych układach izolowanych zawsze rośnie, jest to taka wielkość, która subtelniej opowiada nam o energii. Bądź była ta zasada tak formułowana, że ciepło nie może przepływać od ciała zimniejszego do cieplejszego. Dobrze wiemy, że ten przepływ w świecie jest w drugą stronę. Ale gdyby mogły istnieć takie przepływy w drugą stronę, że od zimniejszego do cieplejszego, to wówczas można by produkować silniki stu procentowe, ale także takie ekologiczne. Możemy sobie wyobrazić taki silnik, który do statku pobiera wodę z oceanu, kostki lodu wrzuca powrotem i porusza się dzięki temu. Tak dobrze niestety nie jest.

3. Problematyka Ruchu.

1. Opis ruchu w fizyce

W fizyce ruchem nazywamy zmianę położenia ciała odbywającą się w czasie postrzeganą przez obserwatora zwanego układem odniesienia.

Rodzaje ruchu:

- ruch ciał mechanicznych(fizyka Newtona),

- ruch fal w powietrzu (typ zmian pewnych wielkości),

- ruch kwantowy ( na poziomie mikroskopijnym),

Jak wygląda matematyczny model, za pomocą którego możemy oddać własność ruchu jako poruszania się ciała materialnego w przestrzeni? Podstawą jest tu model przestrzeni euklidesowej (właściwości):

* ciągłość- przestrzeń ma charakter ciągły pomiędzy dwiema chwilami bliskimi sobie jest zawsze jeszcze inna chwila.

* homogeniczność- czyli przestrzeń jest jednorodna w każdym punkcie bez względu na kierunek poruszania się.

* izotopowość- żaden z kierunków nie jest wyróżniony.

Wyobrażenia nasze o ruchu zostały ukształtowane w pewien sposób przez kształt naszym narządów zmysłowych w kontakcie z rzeczywistością. Zostaje ona zbudowana przez doświadczenie mechaniczne (wielkość, ilość, skalę). Wyobrażenia nasze o ruchu punktu mechanicznego wkładamy w miejsca trudne do wyobrażenia np. świat mikroskopijny bo można zapisać wzorem ruch fal elektromagnetycznych ale trudno je sobie wyobrazić.

W filozofii:

Ruchem nazywamy zmianę bądź miejsca w przestrzeni, bądź ilościową, jakościową, bądź istotną lub powierzchniową, której podlega wszystko, co jest skończone. Problematyka ruchu została poruszona już w starożytności:

• Heraklit - podkreślał, że zasadniczą cechą rzeczywistości jest dynamizm. Zwrócił uwagę na zmienność, na nieustanną ruchliwość (wszystko, co istnieje porusza się, zmienia, przeobraża). Stąd: panta rhei - „wszystko płynie i nic nie trwa”, a także „nie wchodzi się dwa razy do tej samej rzeki”. Dla niego stawanie się jest nieustanną walką, ścieraniem się przeciwieństw.

• Parmienides - teza przeciwna do myśli Heraklita tzw. parmenidejska zasada prawdy: „byt jest i nie może nie być; nie-byt nie jest i nie może w żaden sposób być”. Byt jest jedyną rzeczą, a ruchu nie ma. W związku z tym byt ma takie własności, że jest niezmienny, absolutny i nie podlega żadnej zmianie.

Zenon z Elei - najwybitniejszy uczeń Parmenidesa, który będzie wskazywał, że nie ma czegoś takiego, jak zmiana, że ruch jest tylko pewnym złudzeniem.

2. Arystotelesowski opis ruchu - idea absolutnego spoczynku

Ruch w sensie możliwości zmiany jest dla Arystotelesa najprostszym argumentem na istnienie miejsca w przestrzeni.

Arystoteles stwierdził: że cokolwiek się porusza musi być poruszone przez coś innego. Wiąże więc poruszanie z siłami. Ciało, na które nie działa żadna siła według Arystotelesa znajdowałoby się w spoczynku. Ale ten spoczynek będzie w takim układzie odniesienia, względem któregoś opisujemy ruch wszystkich przedmiotów. Prowadzi to do wyboru układu odniesienia, który ma charakter absolutny.

3. Zasady względności Galileusza i Einsteina

Jest ona odpowiedzią na model przestrzeni Arystotelesa, która mówi, że istnieje absolutny czas i absolutny spoczynek. Owa zasada względności Galileusza likwiduje absolutny spoczynek. W książce Pt. „Dialogi o systemie kopernikańskim” proponuje eksperyment myślowy: wyobraźmy sobie sytuację, że płyniemy pod pokładem statku w którym nie ma okien. W tym pomieszczeniu widzimy kran, z którego kapie woda i fruwające motyle nad nim statek nie podlega żadnym perturbacją. Stąd Galileusz wyciąga wniosek, że nie ma takiego eksperymentu fizykalnego w tym zamkniętym układzie, którym jest pokład statku, za pomocą którego moglibyśmy powiedzieć, że ten układ się porusza ruchem jednostajnym prostoliniowym albo w spoczynku. Nie możemy odróżnić układu poruszającego się od układu spoczynku.

Wszystkie prawa fizyki są takie sam w tych układach, które poruszają się ruchami jednostajnymi prostoliniowymi.

Zasada względności Galileusza, która mówi, że nie potrafimy odróżnić ruchu jednostajnego prostoliniowego od spoczynku. Jest to konsekwencją tego, że układy inercjalne poruszają się względem siebie ze stałą prędkością w jednym kierunku. Te odległości między zdarzeniami nierównoczesnymi będą zależały od układu odniesienia. W zależności, w jakim układzie inercjalnym będziesz siedzieć, to tak będą wyglądać odległości między tymi zdarzeniami nierównoczesnymi.

Zasada Einsteina

Einsteinowska zasada względności postuluje, że dowolne prawo przyrody ma jednakową postać we wszystkich inercjalnych układach odniesienia.

Osoby, które z fizyką dawno nie miały do czynienia mogą niepokoić się użytym tu terminem „inercjalnych”. Oznacza on po prostu, że mówimy tylko o takich układach odniesienia, które same nie poruszają się ruchem przyspieszonym.

Einstein dokonuje uogólnienia zasady Galileusza. W układach inercjalnych wszystkie zjawiska elektryczne, magnetyczne, mechaniczne, fundamentalne równia, które je opisują będą miały taką samą postać.

Na początku XX w. Albert Einstein postawił tezę, że za pomocą nie tylko zjawisk mechanicznych ale wszystkich elektromagnetycznych nie jesteśmy w stanie odróżnić tych układów inercjalnych. Zjawiska elektromagnetyczne też będą jednakowo przebiegać we wszystkich układach inercjalnych. Czyli wszystko jedno czy statek będzie się poruszał ruchem jednostajnym prostoliniowym, czy będzie stał w miejscu, to te zjawiska będą takie same.

Zasada równoważności- jednorodne pole grawitacyjne jest równoważne stałemu przyspieszeniu, także takiemu, którego źródłem nie będą żadne siły grawitacji. Lokalnie grawitacja i przyśpieszenie są nieodróżnialne.

Einstein wymyślił tą zasadę, gdy patrzył na faceta, który maluje dach. Wtedy zaczął sobie myśleć, co by ten gościu czuł jakby spadał. Generalnie pytanie jest takie, czy jak on będzie spadał, to czy będzie odczuwał siłę przyciągania grawitacyjnego czy też i nie.

Wymyślił on, że ten spadający facet będzie w stanie ważkości. Czyli te przyspieszenie, którego ten spadający obserwator będzie doświadczał, będzie równoważone przez pole grawitacyjne, w którym ten spadek się dokonuje. W związku z powyższym, nie będzie on doznawał siły grawitacji, co się nam wydaje paradoksalne, bo on spada pod wpływem tej siły. Ten ruch jest jakby pod wpływem tej siły, zaś on nie będzie jej odczuwał. Feinman w swoich wykładach grawitacji wyraża to bardzo dobitnie, mianowicie będzie pisał, że przyspieszenie - ten przyspieszający ruch tego spadającego kasuje siłę grawitacji. To kasowanie stanowi jądro zasady równoważności

d) paradoks „strzały”, paradoks Achillesa i żółwia

PARADOKS ACHILLESA

Bezpośrednich tekstów Zenona z Elei nie posiadamy, ale jest zapis jego paradoksów w „Fizyce” Arystotelesa: „Drugi argument tzw. Achilles, sprowadza się do tego, że w wyścigu najszybszy biegacz nie może nigdy prześcignąć najpowolniejszego. Tym najszybszym jest Achilles, tym najpowolniejszym żółw - stąd nazwa. Ścigający musi najpierw osiągnąć punkt, z którego ścigany już wyruszył (każdy punkt na drodze Achillesa odpowiada punktowi na drodze żółwia, a więc punktów jest tyle samo na drodze Achillesa, co na drodze żółwia), tak że powolniejszy ma zawsze pewne wyprzedzenie.” Strasznie trudno zbić ten argument, ponieważ jak patrzymy na doświadczenie to oczywistością jest, iż Achilles dogoni żółwia, ale jeśli przyjmiemy sposób rozumowania Zenona to nie jest już takie proste. Jeżeli przyjmiemy, że oni wystartowali z dwóch punktów różniących się o jakiś odstęp to, jeśli Achilles dotarł do tego miejsca gdzie był żółw to ten przesunął się do następnego i tak w nieskończoność. Mamy nieskończoną liczbę odcinków drogi, którą Achilles musi pokonać i nieskończoną ilość chwil czasowych. Rozumowanie Zenona ma taki przebieg, że tego nie można zrobić w skończonym czasie, więc go nie dogoni.

PARADOKS STRZAŁY

„Trzeci argument powiada, że mianowicie wypuszczona strzała stoi w miejscu. Wynika to z supozycji, że czas składa się z szeregu „teraz”. Jeżeli się tego nie założy, wniosek nie wyniknie. (…) Zenon twierdzi mianowicie, że skoro wszystko albo zawsze znajduje się w staniu spoczynku, albo w ruchu, i że jest w spoczynku, gdy zajmuje równą sobie przestrzeń, a to, co jest w ruchu, znajduje się zawsze w jakimś „teraz”, wobec tego strzała wypuszczona z łuku stoi w miejscu”. Polega on ta ty, że Zenon rozumuje w taki sposób, iż strzała niby się porusza, a tak naprawdę ciągle jest nieruchomo w miejscu. Jeśli weźmiemy strzałę w jakimś dowolnym momencie (t₁) to strzała niewątpliwie jest wtedy bezruchu (zajmuje jakieś położenie i nie rusza się). Jeśli weźmiemy w innej chwili (t₂) to sytuacja jest podobna. Ruch byłby nieskończoną ilością punktów chwil, w których strzała się nie rusza, więc ruchu nie ma. Rozumowanie pokazuje, że ruch jest czymś iluzorycznym.

5. równania ruchu i problem determinizmu Laplace'a- chaos deterministyczny.

Równania ruchu:

II zasada dynamiki Newtona- Jeśli mamy jakiś punkt obdarzony masą m, to suma sił, które na niego działają, jest równa iloczynowi masy m i przyśpieszeniu.

F(siła)= m (masa) * a (przyśpieszenie)

Arystoteles: cokolwiek się porusza jest poruszane przez coś innego- odnosi się do prędkości; cokolwiek przyśpiesza jest przyśpieszane przez cokolwiek. Siły są proporcjonalne do prędkości.

Newton: siła jest proporcjonalna do przyśpieszenia. Opór zależy od prędkości- im większa prędkość tym większa siła oporu.

Równania ruchu np.

- formuły Maxwella - formuły opisujące wszystkie zjawiska elektromagnetyczne

- równania Schelingera - dotyczy zjawisk kwantowych

Te równania ruchu opisują związki pomiędzy pewnymi wielkościami fizycznymi w zależności od czasu. One będą nam opowiadały jak układ zmienia się w czasie.

Problem Laplace'a

Jest to proces opisu rzeczywistości - wypowiadam ogólną tezę, ze cała rzeczywistość ma charakter opisu deterministycznego. Laplace twierdził, że gdyby istniała istota rozumna, która potrafi objąć wszystkie warunki początkowe mogłaby przewidzieć, co będzie w dowolnie odległej przyszłości i co było w dowolnie odległej przeszłości. Formułka dająca opisać wszystko - znałbym całą przyszłość i przeszłość świata. Laplace właściwości mechaniki klasycznej rozszerza na całą rzeczywistość. Teza determinizmu staję się tezą deterministycznego opowiadania o przyrodzie. Mechanicyzm szerzy się z sukcesami w przyrodzie. Jednak odkrycie nowych reguł w mechanice klasycznej zadaje kłam determinizmowi laplasowskiemu (okaże się, że pomimo znajomości przyczyn, reguł, nie ma przewidywalności, a tym samym determinizmu).

Determinizm Laplace'a (mechaniczny) to teza z końca XVIII wieku, że rzeczywistość jest w pełni zdeterminowana. Jak ta teza powstała ? Najpierw fizycy wykryli, że istnieje w naturze pewna klasa procesów zdeterminowanych, które są dobrze opisane przez równania ruchu. Potem nastąpiło uogólnienie na całą rzeczywistość. Wszystkie obiekty i procesy miały mieć taką własność, a przecież tego nie wiemy.

Pojawia się więc pytanie o zasadność tego twierdzenia. Czy nie nastąpiło nieprawomocne uogólnienie. Krytykę determinizmu można by rozpocząć od tezy.

Nie możliwe jest, żeby nie istniała wolność. Są ludzie. Oni z jednej strony podlegają pewnym determinacją, ale przecież mają też dużą sferę wolności. Tylko, że argument wolności dotyczy świata duchowego, a teza Laplace'a dotyczy świata przyrody. W XVIII w. nie poznano do końca świata. Z argumentem ze świata przyrody trzeba było poczekać do wieku XIX, kirdy tzw. Fizyka statyczna opisuje wielkie konglomeraty cząstek, np.: cząstek gazu, w taki sposób, że nie można dokładnie powiedzieć gdzie dana cząstka się znajduje, ale tylko z pewnym prawdopodobieństwem. Są to tzw. sądy propablistyczne.

Fizycy doszli do tego, że istnieją ogromne skupiska obiektów, że nie ma sensu rozwiązywać dla nich równań Newtona. Na początku XX wieku powstaje mechanika kwantowa zajmująca się obiektami mikroskopijnymi. Jej fundamentem jest też pewne prawdopodobieństwo. Na tym najważniejszym poziomie przyroda z natury rzeczy jest taka, że jest tam strukturalne, ontyczne prawdopodobieństwo.

Świat jest na tym poziomie złożony podany z ogromną dokładnością np. do 15 miejsc po przecinku np. x₀ (0, ….235).

Mamy drugi warunek początkowy, który różni się tylko o ostatnie miejsce po przecinku x_0'= 0, …… 236.

Pewien typ równania ruchu ma taką właściwość, że ewolucja zaczyna się odchylać, np. odkryto, że drobna zmiana warunku pochodną w warunkach pogodowych powodowała kolosalną różnicę (tzw. efekt motyla) przewidywalność przepada.

Widzimy, ze idea ta nie jest słuszna nawet dla wszystkich równań z zakresu mechaniki klasycznej.

Proces zdeterminowany- jest taki jeżeli jego przebieg zarówno w przyszłość jak i przeszłość jest jednoznacznie określony przez stan tego procesu w chwili obecnej.

Pojęcie determinizmu ma pewne elementy składowe:

• musimy znać warunki początkowe

• trzeba znać równanie ruchu ( kształt tych sił, które występują po jednej ze stron równania Newtona)

• przewidywalność- potrafimy przewidzieć zachowanie obiektów zdeterminowanych

Ciekawa rzecz się okazała w drugiej połowie XX w., że ta ekstrapolacja tego determinizmu na całą rzeczywistość przyrody nieożywionej, że ona zostaje zablokowana, że to zablokowanie nie tylko dokonuje się na tym poziomie mikro świata, ale również dokonuje się na poziomie czysto mechanicznej.

Mianowicie pojawia się chaos deterministyczny. Jak mamy do czynienia z jakimś równaniem ruchu, którego warunki początkowe mamy jakieś tam zadane (początkowa prędkość i początkowe położenie), znamy rozwiązanie jakiegoś równania, które ma własność, że opisuje procesy zdeterminowane, to gdzieś tutaj są te początkowe warunki x₀, V₀ i rozwój w czasie tego jak się zmienia prędkość i położenie.

Możemy sobie wyobrazić, że te warunki początkowe znamy z pewnym błędem. Powiedzmy, że zmieniamy je nieznacznie, że do tego x₀ dodamy jakąś malutką wielkość i do tej prędkości początkowej też dodamy jakąś wartość. Są to bardzo malutkie zmiany tych warunków początkowych:

Nasza intuicja nam podpowiada, że jeśli zrobimy taki numer i te warunki początkowe tak zmienione będą tak przedstawione, że mamy:

No i teraz patrzymy, jak będzie wyglądać ewolucja w czasie o tak zmienionych warunkach początkowych. Intuicja nam mówi, że będzie jakoś podobnie się zachowywać jak ten układ przy wyjściowych warunkach x₀, V₀. To rozwiązanie będzie stabilne.

Tymczasem okazuje się, że istnieją układy opisane przez takie równania ruchu, które rzeczywiście mają ten charakter jak równania, gdzie możemy powiedzieć, że opisują one proces zdeterminowany, które są niezwykle wrażliwe na zmianę tych warunków początkowych, że warunki początkowe zmienią się minimalnie, to ewolucja pobiegnie szybko w zupełnie innym kierunku niż ta zmiana dynamiki układu wyjściowego.

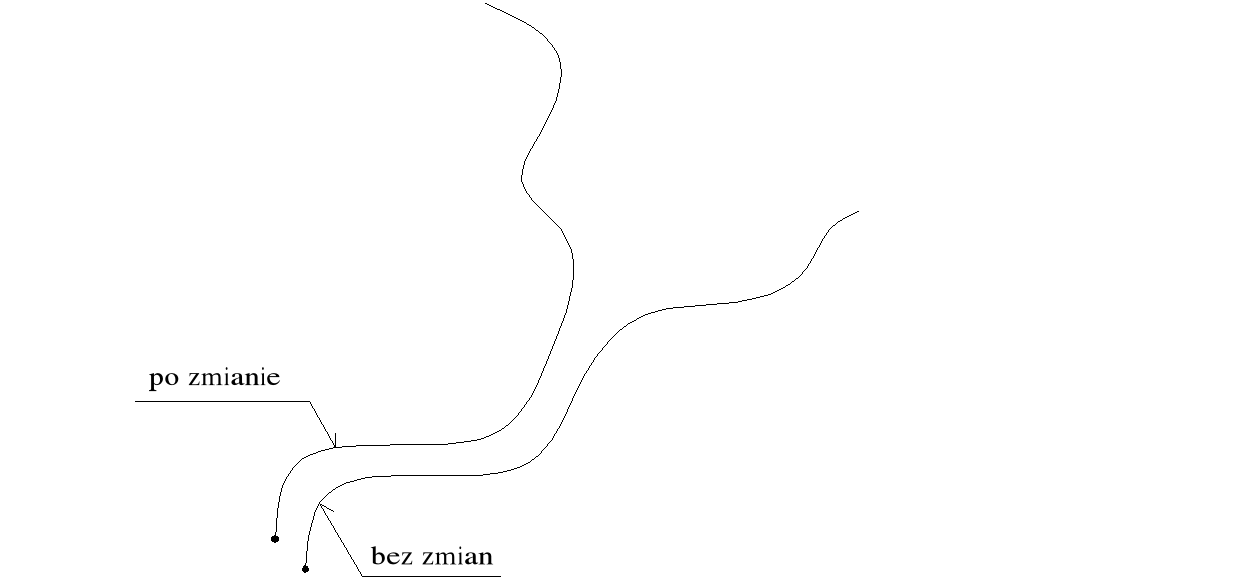
Tą właściwość nazywa się chaosem deterministycznym.

4. KATEGORIA PRAWIDŁOWOŚCI NATURALNEJ

1. forma substancjalna a kategoria prawidłowości naturalnej - matematyzacja opisu procesów fizycznych i prognozy empiryczne

Pojęcie prawidłowości naturalnej. Kategoria, która pojawia się w kosmologii późno. Zastępuje ona kategorię istoty, a precyzyjniej - formy substancjalnej. Ta kategoria ma opisywać z jednej strony zasadę, dzięki której materia czy substancja staje się tym czym jest w tych połączeniach, konkretach bytowych, a z drugiej strony opisuje pewien zespół treści koniecznych i właściwych temu określonemu bytowi. Opisuje pewnego rodzaju zbiór takich treści, które w sposób konieczny i właściwy są związane z takim a nie innym obiektem. Część z filozofów zrozumiała w pewnym momencie życia, że stawiania pytania o istotę jest jałowe. Generalnie właśnie zrezygnowano z tych pytań o istotę, o formę substancjalną, natomiast zaczęto opisywać matematycznie zjawiska fizykalne. Potrzebna jest tutaj kategoria. . I taką kategorią jest ta kategoria prawidłowości naturalnej. Ona jest w sensie znaczeniowym grubo węższa niż forma substancjalna. Forma substancjalna odnosiła się do każdego bytu, natomiast ta kategoria prawidłowości naturalnej odnosi się tylko do reguł ilościowych, które występują w przyrodzie nieożywionej. Ma ona mniejszy zakres, ale ma charakter kategorialny, bo opisuje coś, co jest zupełnie podstawowe.

matematyzacja opisu procesów fizycznych i prognozy empiryczne - od starożytności fizyką zajmowano się w aspekcie jakościowym. Dopiero na początku XIX wieku pojawiają się zręb nowoczesnej nauki. Zostaje wprowadzone pojęcie liczby, miary, masy itd. W eksperymentach zaczyna się mierzyć, liczyć. Jest to już tzw. Zmatematyzowane przyrodoznawstwo - sposób ilościowego opisu świata fizycznego. Dzięki temu potrafimy przewidywać pewnego rodzaju zjawiska fizyczne za pomocą matematycznego opisu świata. Potrafimy przewidzieć ilościowo, co tam wyjdzie.

Prognoza empiryczna - potrafimy z analizy matematycznej wywnioskować „coś” (daną liczbę, co później w eksperymencie się potwierdzi).

2. typologia praw fizycznych - [prawa przyrody to ilościowa relacja pomiędzy wielkościami, które można zmierzyć]

Typologia praw fizyki:

1) Proste zależności funkcyjne np.

- ruch jednostajny prostoliniowy, czyli zależność drogi od czasu (S=vt)

- prawo Ohma - napięcie jest proporcjonalne do natężenia prądu, (U=RI)

2) Równania ruchu np.

- formuły Maxwella - formuły opisujące wszystkie zjawiska elektromagnetyczne

- równania Schelingera - dotyczy zjawisk kwantowych

Te równania ruchu opisują związki pomiędzy pewnymi wielkościami fizycznymi w zależności od czasu. One będą nam opowiadały jak układ zmienia się w czasie.

3) Zasady zachowania np.: energii, momentu pędu, ładunku elektrycznego. Idzie o to, by wyłowić takie wielkości, które będą stałe, niezależne od czasu. Są one bardzo ogólne, słuszne nawet wtedy, gdy opisujemy nieznany fragment świata. W ciemno zakładamy, ze ta zasada tam będzie.

4) Zależności statystyczne

Jest całe mnóstwo układów, do których nie mamy dostępu poznawczego, albo istnieje w nich pewna chaotyczność. Ale jest coś takiego jak rachunek prawdopodobieństwa - próba wyrażenia jakiegoś typu regularności tam, gdzie wydaje się, ze rządzi przypadek

c) struktury matematyczne jako modele rzeczywistości fizykalnej - przestrzeń Euklidesa, Reimanna, modele zjawisk fizycznych: rzut ukośny w próżni, rzut ukośny z uwzględnieniem oporu powietrza, schemat działania modelu w fizyce

Proszę szukać. Brak sił!!!!

Struktura matematyczna - najczęściej: jakiś zbiór elementów, w którego obrębie są określone jakieś relacje, jakieś związki między elementami tego zbioru.

d) filozoficzne ujęcie wzajemnego odniesienia praw do rzeczywistości przyrody nieożywionej

Prawa przyrody- są czymś immanentnym we wszechświecie, są obecne w rzeczywistości, wyrażają coś ważnego w ontologii rzeczywistości w świecie ilościowe relacje po prostu są.

Doniosłość prawa przyrody- przeświadczenie iż regułę rzeczywistości udało się odkryć.

Odniesienie Whiteheada- prawa przyrody zostały nałożone na rzeczywistość.

Prawa przyrody jako kategorie- opisują fundamentalne elementy bytów.

Prawa przyrody zmieniono na kategorie prawidłowości naturalnej. Uważano (Nicole Hartman), że pojęcie formy substancjalnej było przodkiem kategorii praw przyrody.

e) ewolucja pojęcia masy - od Newtona do pól Higgsa

1687 - Newton - ilość substancji jest miarą tejże masy wynikającą z jej gęstości objętości [Jest związana pewną własnością obiektu, nie należy od niczego innego]

Są dwa typy mas: masa grawitacyjna i masa bezwładna. Jedna pojawia się w równaniu siły grawitacji Newtona, druga w II zasadzie dynamiki.

Masa jest pewną własnością obiektu, z tym obiektom integralnie związaną, niezależną od niczego innego poza nim, związana po prostu z jego własnościami

II zasada dynamiki - pojecie masy

Pojawia się współczynnik między przyspieszeniem a siłą, który koreluje, że im większa siła tym większe przyspieszenie. Ten współczynnik modyfikuje te relację:, jeżeli masa jest duża, to trzeba dużej siły, żeby nabrać przyspieszenia, jeżeli masa jest mała to nie trzeba dużej siły. Masa tutaj wiąże się z dynamiką, z ruchem.

Miara bezwładności ciała- pewna właściwość ciała, która określa jak duże przyśpieszenie to ciało może uzyskać, jak dużą siłę trzeba przyłożyć, żeby z góry miało one zadane przyśpieszenie. Nie odwołujemy się tu do objętości ciała, gęstości, tylko ta masa jest wyznaczona przez stosunek siły i przyśpieszenia.

F=ma

Masa wyznaczona przez stosunek siły do przyspieszenia

Związek z oddziaływaniem grawitacyjnym, a nie jakimkolwiek

G- siła grawitacji

r²- kwadrat odległości

m- masa podlegająca sile grawitacji

M- pole grawitacyjne

Masa jest zależna od prędkości. Prędkość staje się funkcją prędkości, z jaką się obiekt z daną masą porusza.

Jest taka zależność, którą można wyliczyć w szczególnej teorii względności. Jak ta zależność funkcyjna wygląda?

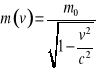
V- prędkość poruszającego się ciała, które ma tzw. masę spoczynkową (czyli masę taką, gdy ciało nie porusza się - m₀;)

C - prędkość światła

m₀- masa bezwładności.

Jak prędkość jest znacząca, to masa tego ciała będzie większa niż masa spoczynkowa.

W momencie kiedy przychodzi szczególna teoria względności to masa staje się funkcją prędkości.

Oczywiście widać, że ten wzór ma też właściwość jak te inne wzory wypisywane, że jeśli prędkość obiekty jest o wiele mniejsza od prędkości światła,

o ta masa (nazywa się relatywistyczną), jest praktycznie masą spoczynkową

Druga ciekawa sprawa przełomowa dla tego pojęcia masy, związana ze szczególną teorią względności, to jest to równanie:

równoważność masy i energii (Einstein). Energia jest równa masie pomnożonej przez kwadrat prędkości świetlnej. Masa jest pewną formą energii. Masę możemy zamienić na energię i energię na masę. Fizyk myśląc o masie myśli o energii.

Dwa typy cząstek elementarnych: masa (elektron, kwark) i nierasowa (foton).

Higgs był takim angielskim fizykiem, który napisał bardzo znaczącą pracę dla myślenia o wszechświecie. W obrębie tego mechanizmu Higgs'a postuluje się, że na początku wszystkie cząstki, kwanty (wszystkie cząstki elementarne są kwantami pewnych pól, które występują w przyrodzie) nie mają żadnych mas. Dopiero musi istnieć specjalny typ pola, który ma taką właściwość, że te cząstki bezmasowe, jak się pojawiają w tym polu, to nabierają masy.

Pole Higgsa - sposób zachowania się pól kwantowych „mechanizm Higgsa” [cząsteczka bezmasowa wpadając w mechanizm Higgsa uzyskuje masowość]

Koncepcja praw natury określa masę w empirystyczny sposób; nie ma sensu stawianie pytań o istotę masy.

f) opis matematyczny a problematyka istoty: ograniczenia metody matematycznej w fizyce

Proszę szukać. Mi się już nie chce.

5. Kategoria oddziaływania

1. Typy oddziaływań

Oddziaływanie- rozpoznajemy siły, jakie działają lub je generujemy. W naszym potocznym poznaniu siła może być przekazywana jedynie w bezpośrednim kontakcie.(np. uderzenie).

Ile takich zupełnie podstawowych oddziaływań istnieje w przyrodzie? Póki co to mamy: grawitacyjne, elektromagnetyczne, słabe i silne. Wielość rozmaitych sił, czy oddziaływań pól, cała ta mnogość rozmaitych zjawisk, daje się sprowadzić do 4 rodzajów oddziaływań.

Warto teraz w paru słowach o tych oddziaływaniach poopowiadać.

Oddziaływanie grawitacyjne jest oddziaływaniem, które zmniejsza się jak 1/r². jest oddziaływaniem niezwykle daleko zasięgowym. Jeśli będzie duża masa w tym liczniku tego mianownika, to to oddziaływanie jest oddziaływaniem, które odpowiada za konstrukcję wszechświata w makroskali. Czyli to, że tworzą się układy planetarne, układy podwójne gwiazd, że gwiazdy wzbijają się w galaktyki, że galaktyki mogą się z sobą przyciągać, za to wszystko odpowiedzialne jest to oddziaływanie grawitacyjne, które ma nieskończony promień oddziaływania.

Elektromagnetyczne oddziaływanie jest odpowiedzialne za wszelkie procesy, które konstytuują atomy, odpowiada za wszelkie możliwe wiązania chemiczne. Za całą mnogość i wielorakość tej rzeczywistości, odpowiedzialne jest to oddziaływanie elektromagnetyczne, które też będzie działać na dowolnie dużych dystansach.

Natomiast zasięg oddziaływania słabego jest 10^-18m, a zasięg oddziaływania silnego to jest 10^-15m. Są to oddziaływania, których fakt istnienia odsłania się dopiero, jak potrafimy prowadzić eksperymenty, gdzie ten rodzaj dystansu jest brany pod uwagę. W przypadku oddziaływań silnych, są to praktycznie oddziaływania między kwarkami, wielkości jądra atomowego i one mają taką własność, że im bliżej siebie te kwarki są, to to oddziaływanie jest słabsze. Jest to tzw. własność asymptotyki oddziaływań. One na większych dystansach praktycznie nie istnieją.

Wszystkie 4 kategorie opisywane są za pomocą pojęcia pola. Pojecie pola dominuje na poziomie kwantowym- mikro. Cząstki kwantowe są kwantami pola- elementami, które przenoszą oddziaływanie pola. Na przykład dla oddziaływania elektromagnetycznego kwantem jest foton, dla oddziaływania elektronowego- elektron. Pola oddziaływują, a cząstki są pośredniczącymi. Oddziaływanie słabe jest znacznie silniejsze niż elektromagnetyczne, ale posiada mały zasięg.

2. idea pola w fizyce

Jak ta idea pola się w ogóle w fizyce pojawia? Otóż zarówno grecy jak i wielu nowożytnych myślicieli (Kartezjusz, młody Newton) uważali, że siła może być przenoszona tylko przy bezpośrednim kontakcie. Trzeba wprawić coś w ruch, udzielić temu jakiegoś pędu. Pierwszym takim miejscem, w którym zaczęło wyglądać, że to nie zawsze tak być musi, że może istnieć tzw. oddziaływanie na odległość, jest analiza siły przyciągania między słońcem a planetami.

Idea oddziaływania niebezpośredniego zaczyna dominować. W fizyce często dokonuje się odkryć z ignorancji. Np. Faraday nie znał matematyki, a wykrył pojęcie pola eksperymentalnie- miał talent do wymyślania eksperymentów. Na szkła rozsypał opiłki metalu, po czym umieścił szkło nad magnesem. Na szkle ułożyły się z opiłków linie sił pola- odkrył zmianę właściwości pola w pobliżu źródła Masy generują siły- siły magnetyczne i elektryczne. Ładunek czy masa jako źródło pola zmieniają właściwości przestrzeni.

Pole jest typem realności. Jest to coś co istnieje rzeczywiście. Pola mają swoją własną energię. Pole pojawia się bez źródeł- niezależnie. Idea pola ostatecznie dotknie teorii grawitacji. Ogólna teoria względności to teoria pola grawitacyjnego.

Pole jest czymś, co realnie istnieje i jest rozciągłe w przestrzeni.. Jest pewnego rodzaju realnością i można o nim myśleć w oderwaniu od źródła (np. fale przemieszczające się w przestrzeni z dala od źródła).

Jako, że Faraday nie znał matematyki, więc nie umiał tego pola w żadnej matematycznej postaci przedstawić. Dokonał tego Maxwell.

Maxwell (klasyczna elektrodynamika) definiował pole jako obiekt, który jest w przestrzeni. Można go opisać matematycznie przez potencjały lub zaczynając od tzw. równań Maxwella. Te równania opowiadają o źródłach. Pierwsze opisuje ładunek generujący pole (źródło). Drugie równanie opisuje nam, że nie ma osobno bieguna magnetycznego. Zawsze pojawia się para biegunów.

3. pojęcie „oddziaływania” u N. Hartmana

W fizyce zaczyna się badać pojęcia fizyczne i pojawiają się pojęcia kategorii. Kategoria oddziaływania pojawia się u Kanta. Kontynuuje on mechanikę Newtonowską (III zasada dynamiki). Do Kanta istnieje tylko kategoria przyczynowa. Kategoria przyczynowa i skutkowa są kategoriami opisującymi świat. Hartman mówi, że oddziaływanie wzajemne to splot nici przyczynowych. Oddziaływania wzajemne znajdują znaczenie nadrzędnej selektywnej zasady ontologicznej - zasady wykluczania. Wykluczane jest to, co się realnie nie wydarzy. Oddziaływania wyznaczają to, co jest możliwe w świecie przyrody nieożywionej.

4. symetrie i idee spontanicznego łamania symetrii dla oddziaływań zunifikowanych

(* tego zagadnienia chyba na wykładach nie było, ale cóż)

Symetria- przedmiot jest symetryczny, jeśli istnieje coś (transformacja), co można z nim zrobić w taki sposób, że po zrobieniu tego (przetransformowaniu) przedmiot wygląda jak przedtem. W symetrii przez poznanie fragmentu złożonego układu poznajemy całość.

6. ELEMENTY FILOZOFII MATEMATYKI

a) Struktura matematyczna i ich badanie

Struktura matematyczna najczęściej: jakiś zbiór elementów, w którego obrębie są określone jakieś relacje, jakieś związki między elementami tego zbioru.

b) Obiekty matematyczne a rzeczywistość fizyczna - idea niezbywalności matematycznego opisu (H. Putnam), niezwykła skuteczność matematyki (E. Wigner)

Pogląd Hilarego Putnama - możemy wyjść z faktu, że matematyka jest intensywnie używana w fizyce i ma tam swoje sukcesy. Można zacząć próbować patrzeć na to użycie matematyki w fizyce, jako na pewnego rodzaju argument na rzecz uznania jakiejś formy istnienia obiektów matematycznych. Wymyślił on argument z niezbędności - jest to argument na rzecz realizmu obiektów matematycznych:

1. gdy zaakceptujemy teorie fizyczne, to zarazem zaakceptujemy teorie o istnieniu bytów matematycznych (gdyż w fizyce używa się intensywnie matematyki)

2. jeśli uznalibyśmy fikcyjność w kwestii istnienia tych obiektów matematycznych, to grozi nam, że znowu, ponieważ te teorie matematyczne są używane w fizyce, ta fikcja w kwestii obiektów matematycznych, pociągnie za nami fikcje w kwestii tych teorii fizycznych.

3. odnosi się też do sposobu uprawiania matematyki. Istnieje sposób aksjomatyczno - dedukcyjny uprawiania matematyki. Ma ona taką właściwość, że jak się udowodni coś w obrębie tej metody, to my wiemy, że tak będzie zawsze. Metoda dedukcyjna jest takim modelem myślenia, który jest niezawodny. Myślenie indukcyjne natomiast może być logicznie zawodne.

E. Wigner napisał artykuł „O niepojętej skuteczności matematyki w naukach przyrodniczych”. Pisze, że jeśli patrzymy na to biorąc abstrakcyjność struktury, w których nie ma żadnego dobrego powodu, żeby sądzić, że one mają jakiś związek ze światem realnie istniejącym, że ostatecznie okazuje się, że te abstrakcyjne struktury pasują do tego świata realnego, to jest jakiś element cudowności, tajemniczości. Jest jakaś część wspólna, jest ileś tworów matematycznych, które w żaden sposób nie są stosowane do opisu świata przyrodniczego. Nie można wykluczyć, że istnieją jakieś twory fizykalne, które matematycznie opisywane nie są. W tym sensie właśnie jest bezpiecznie myśleć w taki sposób, że te 2 światy jakoś na siebie nachodzą, jakoś się przecinają, i z powodu faktu tego przecięcia, możemy wnosić o niezależnym istnieniu tych obiektów matematycznych.

c) Pojęcie nieskończoności: zbiory nieskończone, równoliczność, przeliczalność, nieprzeliczalność

Pojęcie nieskończoności. Najprostsze dojście do pojęcia nieskończoności jest przez negację tego, co skończone. Doświadczenie nieskończoności jest bardzo bogate. Przez zanegowanie pojęcia, jakim jest pojęcie skończoności, dostajemy pojęcie nieskończoności, jako tego, co jest zaprzeczeniem tego, co skończone.

Zbiór nieskończony - jest zespołem obiektów, dla którego można ustalić wzajemnie jednoznaczną odpowiedniość pomiędzy nim a jego częścią.

Równoliczność zbioru - zbiory x i y nazywamy równolicznymi, jeśli istnieje funkcja różnowartościowa, przekształcająca zbiór x na zbiór y.

Zbiór przeliczalny - nazywamy nim zbiór równoliczny ze zbiorem liczb naturalnych lub zbiorem skończonym.

Nieprzeliczalność. Cantor podał przykład zbioru nieprzeliczalnego, czyli takiego, który ma inny typ nieskończoności niż wszystkie ułamki, wszystkie liczby naturalne, całkowite itd.

Jak weźmiemy liczby z odcinka [0,1], to będziemy mieć ułamki, które możemy sobie zapisywać w taki sposób, że po 0, będą występowały liczby od 1 do 9 i będzie ich nieskończenie wiele i nie wykryjemy tu żadnej regularności, żadnych okresów.

d) Filozoficzna typologia nieskończoności w ujęciu G. Cantora (list do Eulenburga)

Cantor mówi, że o nieskończoności potencjalnej tylko dlatego, że istnieje skończoność aktualna (pod terminem nieskończoność aktualna, należy rozumieć wielkość, która z jednej strony jest niezmienna, we wszystkich swych częściach stała i określona, która jest prawdziwą stalą, jednocześnie też przekracza każdą wielkość skończoną tego samego rodzaju). Gdyby nieskończoności aktualnej nie było, to za bardzo nie można by mówić o tej nieskończoności potencjalnej. Jesteśmy zmuszeni do dokonania pewnej fundamentalnej dystynkcji, odróżniając: powiększaną nieskończoność aktualną - pozaskończoność i niepowiększalną nieskończoność aktualną - absolut. Mamy nieskończoność potencjalną, w sensie pojęciowym i mamy 2 typy nieskończoności aktualnej. Z jednej strony to wszystko, czym zajmuje się teoria nieskończoności Cantora - pozaskończoność i absolut. Bogata dziedzina różnych nieskończoności jak alef0, continuum i różnych liczb kardynalnych, które Cantor odkrył, zbadał, w jakiś sposób według niego jest takim oznajmieniem wspaniałości i nieskończoności Stwórcy, do którego to nieskończoności odnosi się pojęcie absolutu, czyli tej wielkości, którą po prostu matematycznie nie da się wyrazić.

e) Platonizm i konstruktywizm

Czy obiekty matematyczne istnieją w jakiś idealny sposób, czy to są po prostu konstrukty, które my wymyślamy? Odpowiedź występuje pod hasłem dwóch przeciwnych poglądów filozoficznych: platonizm kontra konstruktywizm. Z jednej strony jest taki sposób taktowania tych obiektów matematycznych jako obiektów idealnych, które mają jakiś sposób istnienia, platonizm wyrasta z intuicji. A drugi pogląd powiada, że to nie istnieje, nie ma takiego charakteru obiektywnego, niezależnego sposobu istnienia, tylko jest czymś skonstruowanym. Konstruktywista powie, że z matematyki usuwa się to, co nie jest do sprawdzenia (np. nie można zapytać czy liczba jest pierwsza czy nie). Negują prawo wyłączonego środka, dowodzą istnienia obiektów, nie wiedząc jak to jest (dowodzenie wprost).

f) Idea pojęcia prawdopodobieństwa: paradoks Bertranda, definicja Laplace'a, aksjomatyczne ujęcie Kołomogorowa

Paradoks Bertranda (miał znaczenie w rozwoju rachunku prawdopodobieństwa). Pokazuje kłopot dowolności wyboru prawdopodobieństwa. Należy obliczyć prawdopodobieństwo tego, że dowolnie wybrana cięciwa koła o promieniu r będzie większa od boku trójkąta równobocznego wpisanego w to koło.

1. Za miarę przyjmujemy odległość od środka koła.

Możliwa długość d 0 ≤ d ≤ R

Sprzyjające długości d 0 ≤ d ≤ ½ R

Prawdopodobieństwo P = ½ R / R = ½

2. Określamy miarę zdarzeń sprzyjających za pomocą kąta, który pojawia się za pomocą dwóch promieni.

Analogicznie jak wyżej:

0 ≤ α ≤ π

2/3 π ≤ α ≤ π

P=1/3π /π =1/3

Na tym przykładzie widać, że prawdopodobieństwo nosi w sobie aspekt doświadczalności. Nie wiemy, jakie to prawdopodobieństwo jest. Paradoks pokazuje swobodność wyboru miary prawdopodobieństwa.

Prawdopodobieństwo La Place'a określa się w taki sposób:

Prawdopodobieństwo wylosowania asa z talii 56 kart:

Pojęciem takim, które ten ilościowy charakter oddaje w tym nowym ujęciu, jest właśnie pojęcie prawdopodobieństwa. Pojęcie prawdopodobieństwa Laplace'a ograniczone jest do skończonej kolekcji, do takiego zbioru, gdzie liczba możliwości jest skończona.

Aksjomatyczne ujęcie Kołmogorowa

Sformułował on, w jaki matematyczny sposób określamy zbiór wszystkich zdarzeń. Określamy funkcję o własnościach:

1. p = 0 zdarzenie niemożliwe,

2. Jeśli liczba zdarzeń sprzyjających jest równa zdarzeniom możliwym mamy pewność p=1,

3. Ta funkcja musi przyporządkowywać wartości pomiędzy 0 a 1 (odcinek (0,1)),

4. Mamy sumę zdarzeń prawdopodobnych: prawdopodobieństwu sumy zdarzeń jest równa suma prawdopodobieństw zdarzeń (addytywność)

g) Prawdopodobieństwo a rzeczywistość: igła Buffona, prawdopodobieństwo apriori i aposteriori, prawdopodobieństwo w fizyce statystycznej i mechanice kwantowej, „skłonność” K. Poppera

Igła Buffona

Wyobraźmy sobie taką sytuację, że mamy poliniowany papier w taki sposób, że linie są równoległe i jest ustalona odległość między tymi liniami (ciągle taka sama - L). Rzucamy teraz na tą płaszczyznę igłę o długości l. Igła będzie spadać w różne miejsca, różne będzie jej położenie.

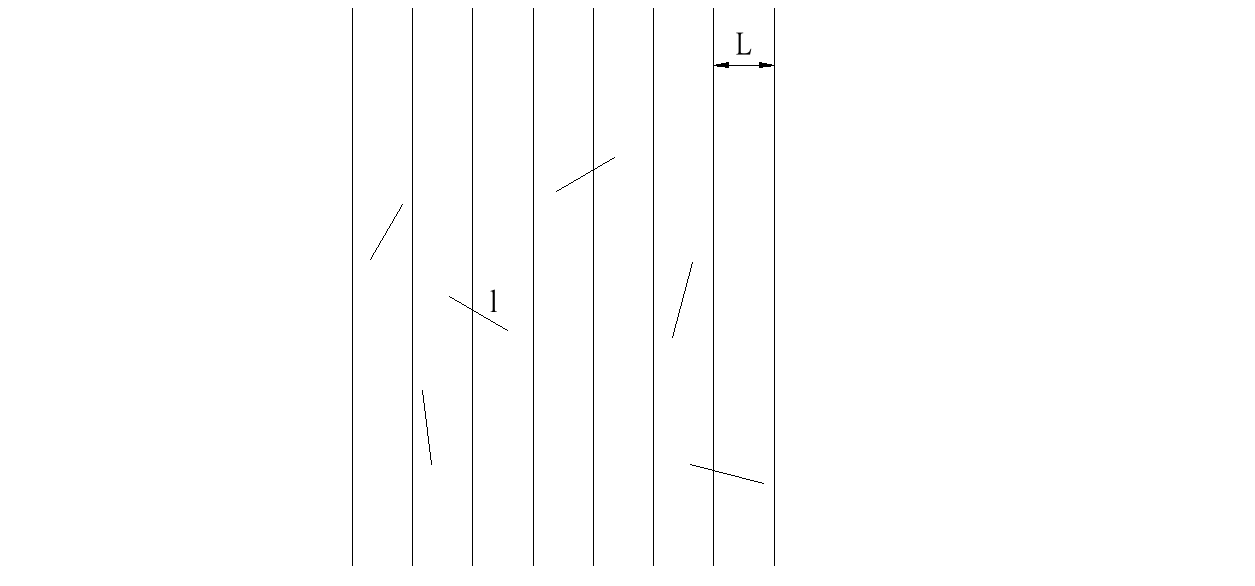
Możemy zadać pytanie, jakie jest prawdopodobieństwo tego, że ta igła przetnie którąś z tych linii równoległych?

Trzeba określić jakieś miary wszystkich zdarzeń możliwych i wszystkich zdarzeń sprzyjających.

Wynik mianowicie wychodzi taki:

p=

Można zrobić taki eksperyment, że poliniujemy sobie papier tak jak w tym zadaniu z jakąś tam odległością, weźmiemy igłę, zmierzymy jej długość i dokonamy jakiejś ilości rzutów. Będziemy wtedy zliczali, że jak np. wykonałem 100 rzutów, to na te 100 rzutów 30 było tych zdarzeń sprzyjających, że igła znalazła się akurat na którejś z linii. Jeśli z tego wzoru wyliczymy
, to się okaże, że przy dostatecznie dużej ilości rzutów, rzeczywiście dostaniemy 3,14, coś koło tego.

Prawdopodobieństwo apriori i aposteriori

Prawdopodobieństwo pojawia się jakby na 2 sposoby:

- prawdopodobieństwo w sensie aposteriorycznym

- prawdopodobieństwo apriorycznym

Czym te 2 pojęcia się odróżnia? Przede wszystkim tym, że biorą się skądinąd. Jedno się bierze z sekwencji wykonywanych eksperymentów, a drugie z teoretycznych obliczeń. W pewnych sytuacjach potrafimy podać prawdopodobieństwo aprioryczne i potrafimy poprzez eksperyment również wyliczyć prawdopodobieństwo aposterioryczne. Ale może być taka sytuacja, że tego prawdopodobieństwa apriorycznego nie potrafimy wyliczyć. Wówczas możemy wyliczać to prawdopodobieństwo aposterioryczne i od tego prawdopodobieństwa iść w stronę tego, że jak coraz dłuższe ciągi prób losowych, to coraz bliżej jesteśmy tego prawdopodobieństwa apriorycznego, którego nie potrafimy wyliczyć, ale zakładamy, że ono jakoś jest.

Bernulli mówi, że określamy jakiś typ częstotliwości zachodzenia zjawiska, które ma taką własność, że prawdopodobieństwa apriorycznego nie znamy i próbujemy szukać jakiejś matematycznej argumentacji na rzecz tego, że rzeczywiście, jak jest dostatecznie duża próba, to my będziemy potrafili oszacować to prawdopodobieństwo a priori, które istnieje gdzieś tam nieznane, poprzez to prawdopodobieństwo aposterioryczne. Jeśli będziemy dokonywać pomiaru prawdopodobieństwa aposteriorycznego, a z drugiej strony mamy jakieś wyliczone prawdopodobieństwo aprioryczne, to musi być jakaś zgodność. Wówczas mamy szansę ujednolicenia, wybrania tego prawdopodobieństwa, które w tej danej sytuacji jest narzucane przez sposób, w jaki my to mierzymy.

Prawdopodobieństwo w fizyce statystycznej i mechanice kwantowej

Gdy pojawiła się mechanika kwantowa, to te 2 rozumienia prawdopodobieństwa wyraźnie się wyklarowały. Z jednej strony jest to, że decydujemy się na opis probabilistyczny, gdyż nie mamy odpowiedniej wiedzy, zaś gdy pojawiła się mechanika kwantowa, to zaczęto się pytać, czy czasem prawdopodobieństwo nie przynależy do struktury rzeczywistości? Świat jest tak stworzony, że on jest probabilistyczny z natury. Na naszym poziomie jest to oczywiście żadną miara nieuchwytne, zaś te obiekty kwantowe będą na swoim poziomie ze swojej natury zachowywać się w sposób przypadkowy.

„Skłonność” K. Poppera

K. Popper wymyślił interpretację skłonnościową. Próbował on myśleć o prawdopodobieństwie jako o pewnego rodzaju dyspozycji obiektu. Ma ono taką właściwość, że jak będziemy obserwowali jego zachowanie, to częstotliwość zachodzenia jakichś zjawisk będzie właśnie taka a nie inna. Np. moneta ma skłonność do spadania z takimi a nie innymi częstotliwościami czy prawdopodobieństwami (p=1/2). Jest to własność monety, że możemy na prawdopodobieństwo popatrzeć w taki sposób właśnie, nie tylko aprioryczny, ale jakby mocniejszy. Że nie tylko umiem wyliczyć, ale że ono tkwi w samej naturze rzeczywistości, że jest cechą samej monety. Dokładnie tak samo będzie się myślało o tych cząstkach kwantowych, że ta cząstka kwantowa ma taką naturę, że z takim a nie innym prawdopodobieństwem będzie się w określony sposób zachowywać. Czyli sprawa tego prawdopodobieństwa, jako elementu ontycznego świata, staje się tutaj niezwykle zasadnicza.

7. Lista pojęć matematycznych:

1. Liczby rzeczywiste, wymierne, niewymierne

Jest to zbiór liczb obejmujący wszystkie liczby wymierne i niewymierne.

Liczby wymierne to zbiór liczb zawierających liczby całkowite i ułamki, natomiast liczby niewymierne to te, których nie możemy wyrazić poprzez ułamek zwykły, liczby niewymierne są tymi ułamkami dziesiętnymi nieskończonymi, które są okresowe.

Zbiór liczb rzeczywistych jest dobrym matematycznym modelem czasu. W tym matematycznym modelu czasu musimy mieć następujące własności:

1. musimy umieć wyróżnić pewien porządek chwil, co było przedtem, co było potem

2. musimy mieć możliwość mierzenia odstępów między chwilami

3. oddawać jednostajny upływ czasu

4. zachować doświadczenie ciągłości

W zbiorze liczb rzeczywistych te właściwości mamy zachowane. Łatwo możemy określić odstęp między chwilami jako wartość bezwzględną dwóch liczb rzeczywistych.

2. Ciąg liczbowy i jego granica ciągu

Mamy następujący ciąg

Zauważamy taką własność, że kolejne liczby tego ciągu są coraz bliżej zera, zmierzają do zera, zaś samo zero do tego ciągu nie należy.

Jak tą własność precyzyjnie wyrazić?

W roku 1821 zostaje podana definicja granicy ciągu przez Couchy'ego:

Dla każdej dowolnej liczby rzeczywistej ε > 0 istnieje taka liczba naturalna N zależna

od ε, że dla każdego n>N zachodzi nierówność

N jest dowolną liczbą i ma określać pewną dokładność zagęszczania się, zbliżania się do liczby a

Od pewnego N wyrazy ciągu należą do odcinka a - ε; a + ε

3. Funkcja

Funkcja - jest to takie przyporządkowanie, które każdemu elementowi ze zbioru X przyporządkowuje dokładnie jeden element ze zbioru Y.

Przykładem funkcji jest przyporządkowanie poszczególnym chwilom punktów w przestrzeni. Jaką zależnością funkcyjną jest ruch jednostajny prostoliniowy, gdze każdej chwili czasowej przyporządkowana jest przebyta odległość.

4. Pojęcie pochodnej funcji jednej zmiennej

Pochodna - opis liczbowy zmiany. Jest to takie pojęcie, które jak mamy do czynienia z jakąś zmiennością to, to pojęcie opowiada o szybkości zmiany tego, co tym parametrem badamy.

Ad1)

Granicą funkcji jest prędkość tego obiektu.

Ad2)

Prędkość ruchu w ruchu jednostajnym prostoliniowym jest proporcjonalna do czasu. Czas rośnie prędkością stałą ciągle krotną o to przyspieszenie ziemskie.

5. Idea równania różniczkowego

Równanie różniczkowe - zależność między funkcjami a jej pochodnymi. Ideą tego równania jest to, aby znaleźć jawną postać tego równania, a nie konkretną wartość.

Jeśli znamy warunki początkowe wiemy, że istnieje rozwiązanie równania różniczkowego co nie znaczy, że możemy osiągnąć tą odpowiedź, czyli jeśli znalibyśmy warunki początkowe danego punktu, to poznalibyśmy całą jego przeszłość i przyszłość. Jeśli cofnąłbym się w czasie i zmieniłbym coś w swoim życiu, to miałoby to wpływ na moje życie obecne.

6. Iloczyn kartezjański zbioru

Iloczynem kartezjańskim dwóch zbiorów X i Y jest zbiór par uporządkowanych (x,y) x ε X i y ε Y

Jeśli mamy pojęcie iloczynu kartezjańskiego, to możemy powiedzieć, co to jest model czasoprzestrzeni Arystotelesa. To jest po prostu iloczyn kartezjański - osi czasu i trójwymiarowej przestrzeni Euklidesowej.

A = TR³

A - czasoprzestrzeń Arystotelesa

T - iloczyn kartezjański

R³ - trójwymiarowa przestrzeń Euklidesowa

7. Przestrzeń metryczna i metryka

W tej przestrzeni mamy do czynienia tylko z odległościami. Odległość między dwoma punktami to długość, liczba, którą przyporządkowujemy a to, co kluczowe dla odległości to przyporządkowanie pewnej liczby.

Przestrzeń metryczna jest to zbiór punktów, na których opisana jest jakaś funkcja, która przyporządkowuje liczby rzeczywiste dodatnie. Ta funkcja nosi nazwę metryki i ma następujące własności:

1. odległość z punktu x do y jest równa 0 wtedy i tylko gdy x = y

2. odległość z punktu x do y jest równa odległości z punktu y do x

3. nierówność trójkąta

W przestrzeni metrycznej nie ma pojęcia przemieszczenia, mamy do czynienia tylko z odległościami. Nie ma w tym modelu dodawania. Ten model jest nieadekwatny do rzeczywistości.

8. Pojęcie grupy i przestrzeń liniowa

W tej przestrzeni wyjściowym zbiorem jest zbiór przemieszczeń:

L = { L₁, L₂,L₃...}

Własności

1. 0 + L = L - przemieszczenie zerowe (operacja dodawania do jakiegokolwiek przemieszczenia nic w nim nie zmienia)

2. L₁ + L₂ = L - dodając przemieszczenia nie wychodzimy poza zbiór L

3. Dla każdego przemieszczenia L istnieje przemieszczenie odwrotne - L. Dodanie tych przemieszczeń do siebie jest równe 0

4. Łączność (wynik nie zależy od kolejności złożeń przemieszczeń)

(L₁ + L₂ ) + L₃ = L₁ + (L₂ + L₃)

9. Pojęcie grupy

Zbiór G z danym działaniem jest grupą wtedy, gdy spełnione są następujące warunki:

1. łączność tego działania (a + b) + c = a + (b + c)

2. element neutralny (taki, który nic nie wnosi), należy do tego układu a + 0 = a

3. istnieje element odwrotny należący do G taki, że:

a + ( - a) = (-a) + a = 0

ten model też nie jest adekwatny. Teraz nie możemy określić odległości. Nie mamy pojęcia kąta, prostopadłości.

10. Przestrzeń euklidesowa

Kartezjusz dokonał algebraizacji geometrii. Zamiast myśleć o geometrii, jak o zbiorze punktów, to teraz myślimy jak o ciągu liczb, które określają współrzędne. Geometria euklidesowa nazywana jest potocznie geometrią cyrkla i linijki.

Kartezjusz wprowadza ideę układu odniesienia. Wyróżnia w przestrzeni jakiś punkt i wiąże z nim coś, co nazywamy układem współrzędnych. W tym układzie każdy punkt daje się opisać parą liczb.

Dowolnemu punktowi możemy przypisać wektor, czyli przemieszczenie i przyporządkowujemy liczbę:

(odległość przemieszczenia od 0 do A)

Możemy zarazem określić przemieszczenie między dwoma punktami:

Możemy też określić coś takiego, jak prostopadłość dwóch wektorów (iloczyn skalarny, jeżeli nie są prostopadłe, to nie jest równe 0)

Przestrzeń euklidesowa, to przestrzeń liniowa i metryczna zarazem. Ale ten model opisuje płaską przestrzeń. Nie występują w niej krzywizny.

11. Zbiory równoliczne i przeliczalne

Równoliczność zbiorów - zbiory X i Y nazywamy równolicznymi, jeśli istnieje funkcja różnowartościowa przekształcająca zbiór X na zbiór Y.

n=n²

f(n) = n

Każdemu n przyporządkowuje się kwadrat.

Zbiory przeliczalne - są to zbiory równoliczne ze zbiorem liczb naturalnych lub ze zbiorem skończonym. Np. trzeba sobie wybrać hotel z nieskończoną ilością pokoi, gdzie wszystkie pokoje są zajęte. Jeżeli przychodzi gość i che nająć pokój to wtedy recepcjonista musi poprosić gościa z pokoju nr 1 aby przeniósł się do pokoju nr 2 itd. Stąd mamy, że suma dwóch zbiorów przeliczalnych jest zbiorem przeliczalnym. Czyli przeliczalne są wtedy, gdy da się je ustawić w ciągu.

12. Zbiór nieskończony w sensie Cantora

Zbiór nieskończony - jest zespołem obiektów dla którego można ustalić wzajemnie jednoznaczną odpowiedniość pomiędzy nim, a jego częścią. Jest to odpowiedź Cantora na paradoks Galileusza.

13. Paradoks Galileusza

Paradoks ten związany jest z nieskończonością. Galileusz w 1638 roku wypisał ciąg liczb naturalnych a pod nimi wypisał ciąg kwadratów tych liczb

X = 1, 2, 3, 4, 5, …

Y = 1, 2, 3, 4, 5, …

Obydwa te zbiory mają taką samą liczebność (są równoliczne). A jednak idąc innym tokiem rozumowania zauważam, że zbiór liczb naturalnych jest „jakoś” większy od zbioru kwadratów. Ten drugi (Y) jest zawarty w pierwszym (X). A przecież istnieje funkcja, która przyporządkowuje każdemu elementowi ze zbioru liczb naturalnych dokładnie jeden element ze zbioru kwadratów: f(n) = n²

Dzięki tej funkcji oba zbiory mają tyle samo elementów.

Jak poradzić sobie z tą sprzecznością?

Poradził sobie z tym Cantor w ten sposób, że wyżej opisany fenomen uczynił definicją zbioru nieskończonego.

14. Prawdopodobieństwo Laplace'a

Wychodząc od klasycznej definicji prawdopodobieństwa, że jest ono ilościowym traktowaniem możliwości, potrzebnym przy prawidłowościach natury statycznej. Potocznie istnieje możliwość matematyczna (bardziej lub mniej możliwe - bardziej lub mniej prawdopodobne = opis probabilistyczny). Są konkretne sytuacje podczas badania świata, gdzie się to zauważa. W ten sposób pojawia się pojęcie przypadku. Zazwyczaj procedury matematyczne upraszczają opis rzeczywistości, w badaniu przypadku wybiera się szczególny podzbiór - proste kolekcje możliwości. Sformułowanie Laplace'a czyli stosunek ilości zdarzeń korzystnych do ilości wszystkich zjawisk jest apriorycznym prawdopodobieństwem, gdyż potrafimy zawczasu podać formułę do zjawisk.

Prawdopodobieństwo - ilość przypadków zdarzeń sprzyjających / ilość zdarzeń możliwych (4 asy / 52 karty).

Pojęcia, które się proszą, aby je znać:

1. Zasady dynamiki Newtona - trzy zasady leżące u podstaw mechaniki klasycznej sformułowane przez Isaaca Newtona i opublikowane w Philosophiae Naturalis Principia Mathematica w 1687 roku. Zasady dynamiki zwane są też prawami ruchu.

I zasada dynamiki (zasada bezwładności)

Jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

O takim ruchu mówimy czasem jako o ruchu swobodnym.

Dlatego pierwsza zasada dynamiki jest traktowana jako postulat istnienia inercjalnego układu odniesienia i jest formułowana:

Istnieje układ odniesienia, w którym ciało nie podlegające oddziaływaniom zewnętrznym spoczywa lub porusza się po prostej ze stałą prędkością.

Jeżeli istnieje jeden inercjalny układ odniesienia, to istnieje ich nieskończenie wiele. Układy inercjalne spoczywają lub poruszają się względem siebie po linii prostej ze stałą prędkością.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa
jest różna od zera), to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej

Współczynnik proporcjonalności jest równy odwrotności masy ciała.

W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki), obowiązuje dla ciała o zmiennej masie np w mechanice relatywistycznej:

Zmiana pędu ciała jest proporcjonalna do działającej siły wypadkowej.

Przy prędkościach, w których nie występują efekty relatywistyczne czyli dla prędkości znacznie mniejszych od prędkości światła, zasadę tę można wyrazić w wersji uproszczonej (ta wersja funkcjonuje na wstępnych etapach nauczania fizyki i jest stosowana powszechnie do obliczeń):

Przyspieszenie z jakim porusza się ciało jest proporcjonalne do działającej siły a odwrotność masy jest współczynnikiem proporcjonalności. Kierunek i zwrot przyspieszenia jest zgodny z kierunkiem i zwrotem siły.

III zasada dynamiki (zasada akcji i reakcji)

Oddziaływania ciał są zawsze wzajemne. Siły wzajemnego oddziaływania dwóch ciał mają takie same wartości, taki sam kierunek, przeciwne zwroty i różne punkty przyłożenia (każda działa na inne ciało).

Jeśli ciało A działa na ciało B siłą F (akcja), to ciało B działa na ciało A siłą (reakcja) o takiej samej wartości i kierunku, lecz o przeciwnym zwrocie.

III Zasada dynamiki, słuszna tylko w mechanice nierelatywistycznej, zwana jest zasadą akcji i reakcji. Zasada ta zakłada, że oddziaływania rozchodzą się w przestrzeni z nieskończoną prędkością. Doświadczenia wskazują, że wszystkie oddziaływania rozchodzą się ze skończoną prędkością nieprzewyższającą prędkości światła.

Zgodnie ze współczesnymi poglądami w zasadach dynamiki należy rozumieć: ciało - punkt materialny, ruch - ruch względem układu odniesienia będącego układem inercjalnym.

Zasady dynamiki mają swoje wersje także dla ruchu obrotowego (punktu i bryły) oraz mogą być stosowane w układach nieinercjalnych po uwzględnieniu sił bezwładności.

2. Ogólna teoria względności (OTW) jest popularną nazwą dla teorii grawitacji opublikowanej przez Alberta Einsteina w 1916 roku. Zgodnie z ogólną teorią względności, siła grawitacji wynika z lokalnej geometrii czasoprzestrzeni. Aparat matematyczny tej teorii został opracowany w pracach takich matematyków jak János Bolyai, a także Carl Gauss. Ogólnie geometria nieeuklidesowa została rozwinięta przez ucznia Gaussa, Georga Bernharda Riemanna, ale nieeuklidesowa geometria czasoprzestrzeni stała się znana szerzej dopiero po tym, jak w opracowaną przez Einsteina szczególną teorię względności Hermann Minkowski wprowadził Czasoprzestrzeń Minkowskiego.

Teoria Einsteina zawiera nietrywialne treści fizyczne dotyczące koncepcji czasu, przestrzeni, geometrii czasoprzestrzeni, związków masy bezwładnej i ważkiej oraz spostrzeżenia dotyczące równoważności grawitacji i sił bezwładności. Jest ona uogólnieniem Szczególnej Teorii Względności obowiązującej dla inercjalnych układów odniesienia na dowolne, także nieinercjalne układy odniesienia. W warstwie matematycznej korzysta ona obficie z metod rachunku tensorowego, geometrii nieeuklidesowej, teorii przestrzeni Riemanna itp.

3. Przestrzeń Riemanna - jest to nazwana od nazwiska Bernharda Riemanna rzeczywista rozmaitość różniczkowa (M, g), dla której zdefiniowany jest tensor metryczny g, oraz istnieje funkcja d(x,y) określająca najkrótszą możliwą krzywą łączącą punkty x i y jako rzeczywistą nieujemną wartość.

4. OTW Einsteina (ogólna teoria względności):

Podstawową ideą teorii względności jest to, że nie możemy mówić o wielkościach fizycznych takich jak prędkość czy przyspieszenie, nie określając wcześniej układu odniesienia, oraz że układ odniesienia definiuje się poprzez wybór pewnego punktu w czasoprzestrzeni, z którym jest on związany. Oznacza to, że wszelki ruch określa się i mierzy względem innych określonych układów odniesienia. W ramach tej teorii, inaczej niż w szczególnej teorii względności, która podawała opis ruchu w inercjalnych (nie posiadających przyspieszenia) układach odniesienia, opis ruchu prowadzony jest w dowolnych układach odniesienia, inercjalnych lub nieinercjalnych. Podstawowym założeniem jest takie sformułowanie praw fizycznych i opisu ruchu aby miały one identyczną postać matematyczną bez względu na używany do opisu układ odniesienia, stąd konieczność zastosowania rachunku tensorowego.

OTW mówi, że z daną dokładnością można definiować jedynie lokalne układy odniesienia, dla skończonych okresów czasu i ograniczonych obszarów w przestrzeni. Jest to analogia z rysowaniem map fragmentów powierzchni Ziemi - nie można sporządzić mapy obejmującej całą powierzchnię Ziemi bez deformacji. Zasady dynamiki Newtona są w ogólnej teorii względności zachowane w lokalnych układach odniesienia. W szczególności cząstki, na które nie działa żadna siła, poruszają się po liniach prostych w lokalnych inercjalnych układach odniesienia. Jednak jeżeli linie te się przedłuży, to nie otrzymujemy linii prostych, lecz krzywe zwane geodezyjnymi. Dlatego też pierwsza zasada dynamiki Newtona zostaje zastąpiona przez zasadę poruszania się po geodezyjnej.

Odróżniamy inercjalne układy odniesienia, w których ciała fizyczne nie zmieniają swojego stanu ruchu, jeżeli nie oddziałują z żadnym innym ciałem fizycznym, od nieinercjalnych układów odniesienia, w których poruszające się ciała mają przyspieszenie pochodzące od układu odniesienia. W tych drugich pojawia się pozorna siła wynikająca z przyspieszenia samego układu odniesienia, a nie z oddziaływania z innym ciałem fizycznym. W związku z tym np. odczuwamy siłę odśrodkową wtedy, gdy samochód, będący naszym układem odniesienia, skręca. Podobnie obserwujemy siłę Coriolisa i siłę odśrodkową wtedy, gdy układem odniesienia jest ciało będące w ruchu obrotowym (na przykład bąk-zabawka lub Ziemia). Zasada równoważności w ogólnej teorii względności mówi, że w układzie lokalnym nie można przeprowadzić doświadczenia, dzięki któremu dałoby się odróżnić spadek swobodny w polu grawitacyjnym od ruchu jednostajnego przy braku pola grawitacyjnego. Mówiąc w skrócie, w układzie odniesienia związanym z ciałem spadającym swobodnie nie ma grawitacji. Oznacza to, że obserwowana na powierzchni Ziemi grawitacja jest siłą obserwowaną w układzie odniesienia związanym z materią na powierzchni, która nie jest "wolna", lecz na którą oddziałuje materia z wnętrza Ziemi i sytuacja ta jest analogiczna do sytuacji w skręcającym samochodzie.

Matematycznie, Einstein modeluje czasoprzestrzeń przy pomocy czterowymiarowej pseudo-riemannowskiej rozmaitości, a jego równanie pola mówi, że krzywizna rozmaitości w punkcie jest bezpośrednio związana z tensorem napięć-energii w tym punkcie; tensor ten jest miarą gęstości materii i energii. Krzywizna określa sposób, w jaki materia się porusza, a materia określa sposób, w jaki przestrzeń się zakrzywia. Równanie pola nie jest dowiedzione w sposób jednoznaczny i istnieje możliwość zaproponowania innych modeli, pod warunkiem, że nie będą stały w sprzeczności z obserwacjami.

Ogólna teoria względności wyróżnia się spośród innych teorii grawitacji swoją prostotą powiązania materii i krzywizny, chociaż wciąż nie istnieje teoria unifikacji pomiędzy ogólną teorią względności, a mechaniką kwantową i nie umiemy zastąpić równania pola bardziej ogólnym prawem kwantowym. Niewielu fizyków wątpi w to, że taka teoria wszystkiego będzie zawierała w sobie ogólną teorię względności, tak jak ogólna teoria względności zawiera w sobie prawo powszechnego ciążenia Newtona w zakresie nierelatywistycznym. Równanie pola Einsteina zawiera parametr zwany stałą kosmologiczną Λ, która została wprowadzona przez Einsteina po to, aby Wszechświat pozostał statyczny (tzn. nierozszerzający i niezapadający się). Ta próba zakończyła się niepowodzeniem z dwóch powodów: statyczny Wszechświat opisywany przez tę teorię byłby niestabilny, co więcej, obserwacje prowadzone przez Hubble'a dekadę później pokazały, ze nasz Wszechświat nie jest statyczny, lecz się rozszerza. Dlatego też zrezygnowano ze stałej Λ, lecz ostatnie obserwacje supernowych typu Ia wskazują na to, że być może należy ją ponownie wprowadzić do równań.

5. Szczególna teoria względności (tu STW) - teoria fizyczna, którą stworzył Albert Einstein w 1905 roku. Zmieniła ona podstawy postrzegania czasu i przestrzeni opisane wcześniej w newtonowskiej mechanice klasycznej, tak aby można było usunąć trudności interpretacyjne i sprzeczności pojawiające się na styku mechaniki (zwanej obecnie klasyczną) i elektromagnetyzmu po ogłoszeniu przez Jamesa Clerka Maxwella teorii elektromagnetyzmu.

W 1916 roku Albert Einstein opublikował ogólną teorię względności, będącą rozszerzeniem teorii szczególnej o opis zjawisk zachodzących w obecności pola grawitacyjnego.

6. Równoważność masy i energii jest jednym z najważniejszych wniosków ze szczególnej teorii względności. Wyraża się on przez jeden z najsłynniejszych wzorów w historii ludzkości:

gdzie: E - Energia m - masa, c - prędkość światła w próżni.

Wzór ten mówi, że energia każdego ciała jest równoważna jego masie. Wielkość tej energii w ustalonych jednostkach to wartość masy w tych jednostkach pomnożona przez prędkość światła do kwadratu. Prędkość światła jest tylko współczynnikiem przeliczania masy na energię, w odpowiednio dobranym układzie jednostek miar np. (Jednostki naturalne) w którym prędkość światła jest bezwymiarowa i równa 1, masa jest równa energii.

Albert Einstein oparł swe rozumowanie na dwóch postulatach:

• Zasadzie względności

Zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych — musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki.

• Niezmienność prędkości światła

Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła światła.

Z połączenia postulatów 1 i 2 dojdziemy do wniosku, że światło nie potrzebuje jakiegokolwiek ośrodka (eteru) do rozchodzenia się.

Alternatywna forma założeń Szczególnej Teorii Względności, interesująca szczególnie z teoretycznego punktu widzenia, jest oparta na następujących, prostszych założeniach:

• Zasada względności Galileusza: "Wszystkie układy odniesienia poruszające się względem siebie ze stałą prędkością są równoważne."

• założenie że transformacja pomiędzy tak określonymi układami jest transformacją afiniczną (liniową z ewentualnie wyrazem stałym);

7. Zasady termodynamiki:

Pierwsza zasada termodynamiki to prosta zasada zachowania energii, czyli ogólna reguła głosząca, że energia w żadnym procesie nie może pojawić się "znikąd".

Zmiana energii wewnętrznej układu ΔU = ΔQ + W

Pierwsza zasada termodynamiki pozwala na zdefiniowanie energii wewnętrznej jako funkcji stanu: dla wszystkich procesów prowadzących od pewnego określonego stanu do drugiego, zmiana ΔU ma zawsze tę samą wartość, choć ilości dostarczanego ciepła i wykonanej pracy są na ogół różne dla różnych procesów. W warunkach nieskończenie małych przyrostów, pierwsza zasada termodynamiki jest w tym przypadku wyrażona następująco:

gdzie δQ i δW są "różniczkami niezupełnymi", tj. zależnymi od drogi; dU zaś jest "różniczką zupełną", tj. niezależną od sposobu przebiegu procesu.

Druga zasada termodynamiki stwierdza, że w układzie termodynamicznie izolowanym, istnieje funkcja stanu, zwana entropią S, której zmiana ΔS w procesie adiabatycznym spełnia nierówność , przy czym równość zachodzi wtedy i tylko wtedy, gdy proces jest odwracalny.

Trzecia zasada termodynamiki (zasada Nernsta) może być sformułowana jako postulat: nie można za pomocą skończonej liczby kroków uzyskać temperatury zera bezwzględnego (zero kelwinów), jeżeli za punkt wyjścia obierzemy niezerową temperaturę bezwzględną.

33

x

c t

Gdzie:

c t = czas pomnożony przez prędkość światła

x = jeden z wymiarów przestrzennych

---