7.2. Silniki asynchroniczne

Zad 96

Trójfazowy silnik asynchroniczny typu SZJKe 32a jest przyłączony do sieci o częstotliwości f₁=50Hz. Znamionowa prędkość obrotowa tego silnika wynosi n_N=1400 obr/min.

Określić:

1. liczbę par biegunów i poślizg przy pracy znamionowej;

2. częstotliwość prądu wirnika przy pracy znamionowej.

Symbol SZJKe 32a oznacza silnik asynchroniczny, budowy zamkniętej, jednoklatkowy w odmianie kołnierzowej. Seria konstrukcyjna jest oznaczona literą „e”. Wielkość mechaniczna wynosi 3. Silnik posiada dwie pary biegunów.

Rozwiązanie:

Znamionową prędkość obrotową n_N=1400 obr/min można zamienić na prędkość kątową ω_N wyrażoną w radianach na sekundę

Wartość znamionowej prędkości kątowej ω_N jest dla pracy silnikowej bardzo zbliżona do prędkości synchronicznej, która wynosi

gdzie „p” jest liczbą par biegunów, którą można odczytać z symbolu silnika (przedostatnia cyfra w symbolu). W tym silniku wynosi ona 2.

Ad. a)

Poślizg s_n przy pracy znamionowej oblicza się z zależności

a wyrażony w procentach wynosi:

Ad. b)

Częstotliwość f₂ prądu wirnika oblicza się ze znajomości poślizgu „s” i częstotliwości stojana „f₁”

Odpowiedź:

Ad. a)

Liczba par biegunów p=2, poślizg przy pracy znamionowej
.

Ad. b)

Częstotliwość prądu wirnika przy pracy znamionowej
.

Zad 97

Obliczyć prąd znamionowy silnika asynchronicznego typu SZJLe 32b, jeżeli wiadomo, że moc znamionowa tego silnika P_N=4,2 kW, a napięcie znamionowe ma wartość 220/380 V/V. Współczynnik mocy przy obciążeniu znamionowym wynosi cosϕ_N=0,86. Sprawność silnika przy obciążeniu znamionowym wynosi η_N=84,5 %.

Rozwiązanie:

Prąd znamionowy w jednej fazie stojana silnika asynchronicznego jest określony dla połączenia uzwojeń w trójkąt w przypadku sieci o napięciu przewodowym U=220 V

Przy połączeniu silnika w gwiazdę, gdy mamy do dyspozycji sieć 3-fazową o napięciu przewodowym U₁=380 V prąd silnika jest równy znamionowemu prądowi fazowemu stojana

Przy połączeniu silnika w trójkąt, to znaczy w przypadku gdy napięcie przewodowe sieci jest równe
prąd znamionowy silnika, przy obciążeniu symetrycznym jest
razy większy od znamionowego prądu fazowego

Odpowiedź:

Prąd znamionowy silnika wynosi
.

Zad 98

Na tabliczce znamionowej silnika asynchronicznego typu SZJe14a są podane następujące dane znamionowe:

P_N=0,8 kW, n_N=1400 obr/min, U_1N=220/380 V, I_N=3,8/2,2 A, η_N=75 %, cosϕ_N=0,74, f_N=50 Hz.

1. Jak należy połączyć uzwojenie stojana silnika, jeśli napięcie przewodowe w sieci wynosi 3×220 V, a jak jeśli napięcie przewodowe jest równe 3×380 V?

2. Jaki prąd popłynąłby przez silnik, jeśli przy napięciu przewodowym w sieci równym 3×380 V uzwojenie stojana silnika połączonoby w trójkąt?

3. Jaki prąd popłynąłby przez silnik, jeśli przy napięciu przewodowym w sieci równym 3×220 V uzwojenie stojana silnika połączonoby w gwiazdę?

Rozwiązanie:

Ad. a)

Jeśli napięcie przewodowe sieci jest równe 3×220 V, należy uzwojenie stojana tego wirnika połączyć w trójkąt. Prąd pobierany wówczas przez silnik wynosi:

Jego wartość jest podana zwykle na tabliczce znamionowej.

Jeśli napięcie przewodowe sieci jest równe 3×380 V, należy uzwojenie stojana tego silnika połączyć w gwiazdę. Prąd pobierany wówczas przez silnik jest równy prądowi fazowemu przy połączeniu w trójkąt, a więc

Wyżej wymienioną wartość prądu można również obliczyć z danych znamionowych podanych na tabliczce znamionowej. Znając moc, sprawność i współczynnik mocy, wartość prądu można wyrazić wzorem

Ad. b)

Jeśli uzwojenie stojana tego silnika zostanie połączone w trójkąt, przy napięciu przewodowym sieci równym 3×380 V, to silnik pobiera prąd
razy większy od znamionowego

,

co może być przyczyną uszkodzenia silnika.

Ad. c)

Jeśli uzwojenie stojana tego silnika połączyć w gwiazdę przy napięciu przewodowym sieci równym 3×220 V, to silnik pobiera prąd
razy mniejszy od znamionowego

Takie połączenie stosuje się w przypadkach rozruchu za pomocą przełącznika gwiazda-trójkąt. Wówczas natężenia prądu w momencie rozruchu spada
razy (w stosunku do znamionowego). Natomiast moment zmniejsza się 3 razy.

Odpowiedź:

Ad. a)

Jeśli napięcie przewodowe sieci jest równe 3×220 V, należy uzwojenie stojana tego silnika połączyć trójkąt. Jeśli napięcie przewodowe sieci jest równe 3×380 V, wówczas należy uzwojenie stojana tego silnika połączyć w gwiazdę.

Ad. b)

Przy napięciu przewodowym sieci równym 3×380 V i uzwojeniu stojana silnika połączonym w trójkąt prąd silnika wynosi
.

Ad. c)

W przypadku połączenia uzwojenia stojana silnika w gwiazdę przy napięciu przewodowym sieci równym 3×220 V prąd pobierany przez silnik wynosi
.

Zad. 99

Na tabliczce znamionowej trójfazowego silnika klatkowego z uzwojeniami połączonymi w trójkąt są podane wielkości: znamionowa moc P_N=1,1kW, współczynnik mocy przy obciążeniu znamionowym cosϕ_N=0,86, prąd znamionowy I_N=2,49 A, napięcie przewodowe znamionowe U_N=380 V, znamionowa prędkość obrotowa n_N=1410 obr/min.

1. Obliczyć sprawność tego silnika oraz moment znamionowy na jego wale przy obciążeniu znamionowym;

2. Jaki prąd popłynie, gdy uzwojenia tego silnika połączymy w gwiazdę i jaki powstanie moment na wale?

Rozwiązanie:

Ad. a)

Sprawność silnika przy obciążeniu znamionowym oblicza się za pomocą wzoru:

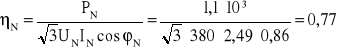
Ad. b)

Gdy uzwojenia silnika połączymy w gwiazdę, przy tym samym napięciu zasilania, to prąd będzie
razy mniejszy od prądu znamionowego

Z uwagi na jednoczesne zmniejszenie napięcia fazowego silnika, a także jego prądu, moment wytworzony na wale silnika jest wówczas 3 krotnie mniejszy od znamionowego.

Odpowiedź:

Najczęściej sprawność podaje się w procentach, czyli sprawność rozważanego silnika wynosi η_%=77 %. Natomiast moment znamionowy wynosi 7,45 Nm. Gdy uzwojenia silnika połączy się w gwiazdę to prąd i moment wynoszą kolejno 1,46 A i 2,5 Nm.

7.2. Prądnice prądu stałego

Zad. 100

Dwie jednakowe prądnice obcowzbudne prądu stałego o danych znamionowych:

P_N=19 kW

U_N=230 V

I_N=82,7 A

n_N=720 obr/min

R_t=0,2 Ω

i identycznych charakterystykach zewnętrznych, pracują równolegle przy prędkości obrotowej znamionowej wzbudzone prądem równym połowie prądu znamionowego I_w=0,5 I_wN. Prądnice są obciążone rezystancją R=1,5 Ω.

Obliczyć:

1. napięcie na zaciskach prądnic po wyłączeniu obciążenia;

2. napięcie na zaciskach i prądy obciążenia prądnic po przerwaniu prądu wzbudzenia w jednej z prądnic;

3. napięcie na zaciskach i prąd obciążenia jednej z prądnic po wyłączeniu drugiej prądnicy.

W obliczeniach założyć linearyzację charakterystyki magnesowania i pominąć oddziaływanie twornika.

Rozwiązanie:

Ad. a)

Po wyłączeniu obciążenia spadek napięcia na rezystancjach tworników jest równy zeru. Napięcie na zaciskach twornika jest równe sile elektromotorycznej. Przy prędkości obrotowej znamionowej i prądzie wzbudzenia I_w=0,5 I_wN napięcie na nieobciążonych prądnicach wynosi

Ad. b)

Schemat zastępczy prądnic pracujących równolegle.

Rys. 100.1

Po wyłączeniu prądu wzbudzenia jednej z prądnic, siła elektromotoryczna na zaciskach jej twornika jest równa zeru E₁=0. Wówczas druga prądnica jest obciążona rezystancją będącą połączeniem równoległym rezystancji obciążenia R i rezystancji twornika R_t1 prądnicy niewzbudzonej (Rys. 100.1).

Prąd obciążenia tej prądnicy można obliczyć z II p. K.

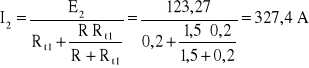
Siła elektromotoryczna w tworniku wzbudzonej prądnicy ma wartość

Napięcie na zaciskach prądnicy wynosi

Prąd płynący przez rezystancję obciążenia wynosi

Prąd twornika prądnicy niewzbudzonej można wyznaczyć z wyrażenia

Ad. c)

Po wyłączeniu, a właściwie odłączeniu pierwszej prądnicy, druga prądnica pracuje na rezystancję R. Wówczas prąd obciążenia można określić ze wzoru

Należy dodać, że prądnica druga zasila odbiornik R napięciem U_o wynikającym z obniżenia prądu wzbudzenia. Wówczas napięcie ma wartość

Odpowiedź:

a)

b)
,
,

c)
,

Zad. 101

Prądnica bocznikowa prądu stałego G (Rys. 101.1), o rezystancji uzwojenia twornika R_t=0,15 Ω i rezystancji uzwojenia wzbudzającego R_w=100 Ω, zasila odbiornik o rezystancji R=5 Ω. Napięcie na zaciskach prądnicy wynosi U=220 V. Obliczyć prąd płynący przez odbiornik I, prąd wzbudzenia I_w, prąd w uzwojeniu twornika I_t, siłę elektromotoryczną prądnicy E.

Rys. 101.1

Rozwiązanie:

Korzystając z praw Kirchhoffa układa się równania dla dwóch oczek i jednego węzła

(1)

(2)

(3)

Napięcie na zaciskach twornika jest pomniejszone o spadek napięcia na jego rezystancji.

Z równania (1) można obliczyć wartość prądu I, a z równania (2) można obliczyć I_w. Z równania (3) można wyznaczyć wartość prądu I_t płynącego przez twornik. W tym celu obliczamy prąd I płynący przez odbiornik

oraz prąd wzbudzenia I_w

Z I p. K. prąd w uzwojeniu twornika I_t jest sumą prądów wzbudzenia i obciążenia

Siłę elektromotoryczną prądnicy można obliczyć z równania (1)

Odpowiedź:

,
,
,
.

7.3. Silniki prądu stałego

Zad. 102

Silnik bocznikowy prądu stałego pracuje w układzie jak na rysunku 102.1. Dane znamionowe: P_N=15 kW, U_N=220 V, n_N=1200 obr/min, η_N=0,86. Znamionowe straty mocy w wirniku ΔP_aN=900 W. Znamionowe straty mocy w uzwojeniu wzbudzenia ΔP_wN=600 W.

Obliczyć:

1. prądy znamionowe wirnika (I_aN) i wzbudzenia (I_wN), rezystancję uzwojenia wirnika i wzbudzenia (R_aN, R_wN), siłę elektromotoryczną E_N i moment M_N w warunkach znamionowych;

2. prędkość obrotową przy obciążeniu silnika momentem M=100 Nm;

3. rezystancję R_d, którą należy włączyć w obwód wirnika, aby przy obciążeniu momentem M=110 Nm uzyskać prędkość obrotową n=1000 obr/min.

Rys. 102.1

Rozwiązanie:

Ad. a)

Prąd znamionowy silnika wyraża się wzorem:

Prąd wzbudzenia w warunkach znamionowych określa się na podstawie danych zadania:

Prąd wirnika w warunkach znamionowych jest różnicą prądu pobieranego przez silnik i prądu wzbudzenia.

Znając znamionową stratę mocy w wirniku i wartość znamionową jego prądu możemy obliczyć rezystancję wirnika:

Rezystancja uzwojenia wzbudzenia wynosi:

Siłę elektromotoryczną zwaną także napięciem indukowanym w wirniku w warunkach znamionowych zasilania i obciążenia określa się z zależności:

Moment znamionowy obliczamy ze wzoru:

Ad. b)

W warunkach znamionowych:

W nowych warunkach pracy:

Dzieląc stronami powyższe równania otrzymamy:

Prąd wirnika przy obciążeniu momentem M=100 Nm wynosi:

Napięcie indukowane w wirniku w nowych warunkach pracy wyznaczamy z poniższej zależności:

Z równań napięć indukowanych:

określa się szukaną wartość prędkości obrotowej:

Ad. c)

Prąd
wirnika można wyznaczyć wykorzystując otrzymane w punkcie b) zależności określające moment M i moment znamionowy M_N:

Napięcie indukowane w wirniku obracającym się z prędkością n=1000 obr/min obliczamy z równań:

Dla obwodu z włączoną rezystancją R_d równanie napięciowe przyjmuje postać:

stąd szukana wartość rezystancji wynosi:

Odpowiedź:

Ad. a)

Parametry znamionowe rozważanego silnika bocznikowego wynoszą:

,
,
,
,
,
.

Ad. b)

Prędkość obrotowa silnika przy obciążeniu nieco mniejszym od znamionowego wzrasta do wartości
.

Ad. c)

Aby uzyskać (znacznie mniejszą od znamionowej) prędkość obrotową 1000 obr/min należy włączyć w obwód wirnika rezystancję o wartości
.

Zad. 103

Silnik bocznikowy prądu stałego (Rys. 103.1) ma włączone rezystancje dodatkowe w uzwojeniach twornika i wzbudzenia. Dane znamionowe silnika mają wartości identyczne jak w poprzednim zadaniu: P_N=15 kW, U_N=220 V, n_N=1200 obr/min, η_N=0,86, ΔP_aN=900 W, ΔP_wN=600 W.

Przy założeniu liniowej charakterystyki magnesowania obliczyć dodatkową rezystancję R_wd w obwodzie wzbudzenia, aby przy obciążeniu momentem M=100 Nm uzyskać prędkość obrotową wirnika n=1400 obr/min.

Rys. 103.1

Rozwiązanie:

Zmniejszenie prądu wzbudzenia powoduje zmniejszenie strumienia magnetycznego Φ, co przy niezmienionym napięciu zasilania skutkuje wzrostem prędkości obrotowej wirnika.

Z równań określających moment maszyny

można wyznaczyć żądaną wartość prądu wzbudzenia I_w. Po podzieleniu tych równań stronami oraz uwzględnieniu wartości momentu obciążenia i momentu znamionowego obliczonego w zadaniu 102 otrzymamy:

Z powyższego można wyznaczyć prąd wzbudzenia, wytwarzający mniejszy strumień magnetyczny:

Po podzieleniu (stronami) równań napięciowych określających napięcie indukowane w wirniku maszyny

otrzymamy zależność:

Podstawiając otrzymane zależności do równania napięciowego określającego indukowane w wirniku napięcie

otrzymuje się wyrażenie zależne od zmiennej wartości prądu wzbudzenia

Po kolejnych przekształceniach otrzymamy równanie kwadratowe:

Rozwiązując powyższe równanie oblicza się dwie wartości prądu:

,

Mniejsza wartość prądu wzbudzenia nie spełnia warunków zadania. Omawiany stan pracy dotyczy wartości prądu wzbudzenia
.

Rezystancja dodatkowa w obwodzie wzbudzenia wynosi:

Wykorzystując wcześniejszą zależność dotyczącą iloczynu prądu wzbudzenia i wirnika, obliczamy prąd wirnika

Odpowiedź:

Rezystancja dodatkowa jaką należy włączyć w obwód wzbudzenia, aby prędkość obrotowa wirnika wzrosła do n=1400 obr/min, wynosi
.

Zad. 104

Silnik bocznikowy prądu stałego o danych: P_N=17 kW, U_N=440 V, I_N=43,4 A, n_N=3000 obr/min, R_a=0,197 Ω pracuje na charakterystyce naturalnej i jest obciążony momentem M₁=0,65 M_N. W celu zatrzymania silnika przełączono go na hamowanie przeciwłączeniem. Określić wielkość momentu rozwijanego przez silnik na początku i końcu hamowania jeżeli w obwód główny włączono rezystancję dodatkową R_d=8,5 Ω. Uwzględnić tzw. straty mechaniczne momentu i założyć równość prądu silnika i wirnika.

Rozwiązanie:

W celu wyznaczenia prądów i momentów obciążenia obliczamy wielkości znamionowe tego silnika.

Moment znamionowy na wale silnika wynosi:

Znamionowa siła elektromotoryczna indukowana w uzwojeniu wirnika wynosi

Moment elektromagnetyczny wytworzony w uzwojeniu wirnika, przy założeniu że prąd wirnika jest równy prądowi silnika, wynosi:

Różnica momentu elektromagnetycznego i momentu na wale silnika zwana stratą momentu jest stosunkowo mała i wynosi:

Moment elektromagnetyczny podczas obciążenia wirnika momentem równym 0,65 momentu znamionowego (na wale), można obliczyć uwzględniając wcześniej obliczoną stratę momentu

Prędkość biegu jałowego n_o nieobciążonego silnika można obliczyć uwzględniając równanie napięciowe wirnika oraz proporcjonalność siły elektromotorycznej w nim wytworzonej do jego prędkości obrotowej

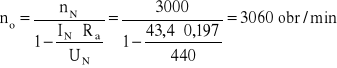
Prąd pobierany przez wirnik podczas obciążenia go momentem M₁ wynosi

Prędkość obrotowa wirnika i siła elektromotoryczna (napięcie indukowane w wirniku) indukowana podczas obciążenia silnika momentem M₁ mogą być wyznaczone z wykorzystaniem równania napięciowego

Rys. 103.1

W czasie hamowania przeciwłączeniem charakterystykę prędkości w funkcji momentu rozwijanego przez silnik n=f(M) przedstawiono na Rys. 103.1. Momentowi początkowemu hamowania M_Hp odpowiada prąd początkowy I_Hp, który można wyznaczyć z równania napięciowego

Końcowy prąd hamowania występuje w momencie całkowitego) zatrzymania silnika (n=0). Wówczas siła elektromotoryczna indukowana w wirniku jest równa zeru E=0. Dlatego też napięcie zasilania jest równe spadkowi napięcia na rezystancji istniejącej w obwodzie wirnika.

Moment na wale w chwili początkowej i końcowej hamowania jest proporcjonalny do prądów

Odpowiedź:

Momenty na wale silnika w chwili początkowej i końcowej hamowania wynoszą:
,
.

Zad. 105

Silnik szeregowy prądu stałego ma dane: U_N=440 V, n_N=1100 obr/min, ၨ_N=0,85, R_a=1,67 Ω, R_w=1 Ω. Zakładając liniowość charakterystyki magnesowania czyli strumienia w funkcji prądu obliczyć:

1. moment przy którym prędkość obrotowa wirnika jest większa od znamionowej i wynosi n=1250 obr/min;

2. obliczyć napięcie jakim trzeba zasilić silnik aby przy momencie obciążenia M=40 Nm zmniejszyć prędkość obrotową silnika szeregowego do wartości n=900 obr/min.

Rozwiązanie:

Ad. a)

Uwzględniając liniowość charakterystyki magnesowania (
) można określić zależność napięcia indukowanego E w wirniku i momentu od prądu silnika. Wówczas siła elektromotoryczna zależy liniowo od prądu i prędkości obrotowej. Natomiast moment zależy parabolicznie od prądu.

W celu wyznaczenia momentu, przy prędkości wirnika n=1250 obr/min, należy określić wartości znamionowe momentu, prądu i siły elektromotorycznej.

Uwzględniając zależność momentu od prądu, można wyznaczyć moment dla innej (niż znamionowa) prędkości obrotowej.

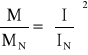
Wykorzystując liniową zależność E napięcia indukowanego w wirniku od jego prądu otrzymuje się:

Uwzględniając równanie napięciowe silnika i wykorzystując powyższe wyrażenie można obliczyć prąd silnika szeregowego

Moment zależy parabolicznie od prądu. Tak więc:

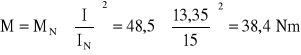
Ad. b)

Uwzględniając liniowość charakterystyki magnesowania oraz wyrażenia określające moment i siłę elektromotoryczną (napięcie indukowane) w wirniku

można wyznaczyć napięcie jakim trzeba zasilić silnik aby przy mniejszym obciążeniu obniżyć jego prędkość obrotową. Jednakże w tym celu należy określić prąd pobierany przez silnik obciążony momentem M=40 Nm.

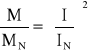
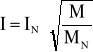
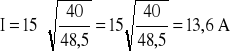
Uwzględniając żądaną prędkość obrotową oraz obliczoną wartość prądu wyznaczamy siłę elektromotoryczną E oraz napięcie.

Odpowiedź:

Ad. a)

Moment obrotowy wirnika silnika szeregowego, przy zwiększonej prędkości znamionowej musi być mniejszy od momentu znamionowego i wynosi:
.

Ad. b)

Aby uzyskać znacznie mniejszą od znamionowej prędkość obrotową wirnika silnika szeregowego, przy obciążeniu go momentem nieco mniejszym od znamionowego, należy znacznie obniżyć napięcie zasilania do wartości:
.

269

269

---