Funkcje kosztów

1. Minimalizacja kosztów

2. Elastyczność substytucji

3. Funkcje kosztów w długim okresie (LR)

4. Funkcje kosztów w długim okresie (LR) i korzyści

skali

☺ Przykład: Wykorzystanie funkcji Cobb-Douglas'a

do estymacji funkcji kosztów w długim okresie

(LR)

5. Koszty w krótkim okresie (SR) przy jednym

zmiennym czynniku

6. Koszty w krótkim okresie (SR) przy dwóch lub

więcej zmiennych czynnikach

7. Zależność między kosztami w długim okresie (LR) i

krótkim okresie (SR)

☻

Minimalizacja kosztów

Funkcja kosztów: najniższe ekonomiczne koszty do produkcji każdego możliwego poziomu produktu.

Zał.: funkcję produkcji reprezentują izokwanty wypukłe względem początku układu współrzędnych; płace i renty są parametrami.

Minimalizacja kosztów - rys. 11.1: linie izokosztów reprezentują poziomy powierzchni funkcji celu dla danego stosunku płac, rent. Izokwanta,
, przedstawia ograniczenie produkcji. Kombinacja czynników prowadząca do minimalizacji kosztów (K*, L*) osiągana jest w punkcie styczności izokwanty i linią izokosztów, TC*.

Warunek styczności można interpretować:

nachylenie izokwanty = dK/dL = -w/r = nachylenie linii izokosztów

MRTS = - (dK/dL) = w/r = MP_L/MP_K.

Powyższe równanie minimalizacji kosztów oznacza, że firma dostosowuje kombinację zatrudnionych czynników aż technicznie wyznaczona MRTS zrówna się ze stosunkiem cen wyznaczonym przez rynek.

Wyprowadzenie:

Funkcja celu: minimalizacja kosztów:

C = r₁x₁ + r₂x₂ + b gdzie: x₁ i x₂ ≥ 0

p.w.: q₀ = f(x₁, x₂) gdzie: q₀ to zadany poziom produkcji, a f(x₁, x₂) jest ciągła i ma ciągłe pochodne cząstkowe pierwszego i drugiego rzędu.

Funkcja Lagrange'a:

F = r₁x₁ + r₂x₂ + b + λ[q₀ - f(x₁, x₂)]

Pochodne pierwszego rzędu przyrównujemy do zera:

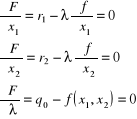
Otrzymujemy z nich:

i

Co jest równoważne:

Alternatywnie można zapisać:

Warunki drugiego rzędu:

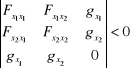
W naszym przypadku powyższy wyznacznik przyjmuje postać:

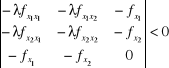
Po przekształceniu:

co jest równoważne:

Z
wiemy, że
. Ponieważ licznik i mianownik są dodatnie, λ też jest dodatnia.

Możemy więc powyższą nierówność podzielić przez λ bez zmiany znaku:

Jest to warunek drugiego rzędu, który musi być spełniony wraz z warunkami pierwszego rzędu.

Przykład:

Funkcja produkcji: x = K^1/2L^1/2

Minimalizujemy koszty przy:
.

Funkcja Lagrange'a:

Warunki pierwszego rzędu:

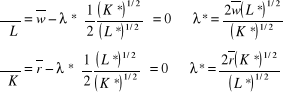
Po zrównaniu wartości λ* otrzymujemy:

Po przekształceniach:

Wstawiając powyższe równanie do trzeciego warunku pierwszego rzędu:

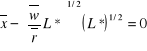
Rozwiązując dla L*:

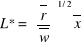
: optymalne zatrudnienie pracy do produkcji

Po wstawieniu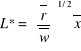
do
:

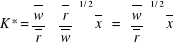
: optymalne zatrudnienie kapitału do produkcji

Po wstawieniu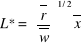
i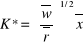
do funkcji celu:

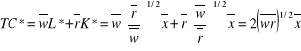
: minimalny koszt wyprodukowania
.

(Pomijamy warunek drugiego rzędu.)

Elastyczność substytucji

W długim okresie firma może dostosowywać kombinację zatrudnienia czynników w odpowiedzi na zmiany stosunku cen rynkowych. Zakres tych dostosowań zależy od techniki produkcji zawartej w izokwantach. Miarą możliwości dostosowań jest elastyczność substytucji wzdłuż izokwanty. Pokazuje ona reakcje minimalizującego koszty stosunku kapitału i pracy na zmiany stosunku cen tych czynników w LR.

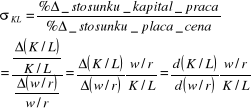
Możemy uprościć zapis formułując nowe funkcje:

oraz
gdzie
.

Po wstawieniu powyższych funkcji do definicji otrzymujemy:

.

Funkcja
została wyprowadzona z warunku styczności, MRTS = w/r. Na przykład jeżeli x = K^1/2L^1/2, to:

MRTS = K/L = w/r ⇒

A więc:

: dla tej funkcji produkcji elastyczność substytucji wynosi 1.

Cechą uogólnionej postaci funkcji produkcji Cobba - Douglasa jest stała jednostkowa elastyczność substytucji. Wyprowadzenie tego wyniku (np. Chiang, str. 425 - 6) nie jest związane z założeniem α + β = 1.

Funkcje CES (constant elasticity of substitution)

Istnieje inna postać funkcji produkcji o stałej elastyczności substytucji, która daje
. Równanie tej funkcji zwanej funkcją produkcji CES:

(A > 0; 0 <
< 1 ; -1 <

)

gdzie: K i L to czynniki produkcji

A,
,
to trzy parametry.

A - parametr efektywności - odgrywa taką samą rolę jak współczynnik A w funkcji Cobba - Douglasa (Q = AK ^αL^β). Wielkość A będzie proporcjonalnie zwiększać poziom Q.

A : służy jako wskaźnik poziomu technologii.

- parametr podziału - dotyczy (jak α w funkcji Cobba - Douglasa) względnego udziału czynników w produkcji.

- parametr substytucji - określa wartość, jaką przyjmie (stała) elastyczność substytucji.

Graniczne przypadki elastyczności substytucji

(Rys. 11.2):

: stałe proporcje czynników (Technologia Leontiefa);

: przy zmianie stosunku cen zmienia się stosunek K*/L* minimalizujący koszty;

: jeżeli nachylenie izokwanty jest takie samo jak linii izokosztów, to kombinacja K/L minimalizująca koszty jest nieokreślona i najmniejsza zmiana nachylenia linii izokosztów zmienia optymalną kombinację czynników z jednej osi do drugiej.

Funkcje kosztów w długim okresie

Ścieżka rozwoju w długim okresie

Konstruujemy funkcję: ścieżkę rozwoju w długim okresie z punktów styczności izokwant i linii izokosztów (rys. 11.3):

(odpowiednik krzywej ekspansji dochodowej)

Z minimalizacji kosztów wiemy, że dla funkcji: x = K^1/2L^1/2 otrzymujemy:

: a jest to ścieżka rozwoju firmy w długim okresie.

Koszty całkowite w długim okresie

Z otrzymanej ścieżki można wyprowadzić funkcje opisujące optymalne czynniki dla każdego poziomu produkcji:

i

oraz minimalne koszty wytworzenia każdego poziomu produkcji (po wstawieniu powyższych funkcji do

):

: koszty całkowite w długim okresie jako funkcja produktu.

(Rys. 11.4 : minimalne koszty wytworzenia każdego poziomu produktu przy wszystkich czynnikach zmiennych: minimalne koszty wytworzenia x₁ wynoszą TC*₁, itd., te koszty całkowite są oznaczone na osi pionowej, a odpowiadające im wielkości produkcji - na poziomej).

Dla x = K^1/2L^1/2 wyznaczyliśmy już optymalną kombinację czynników dla każdego poziomu produkcji,
:

-
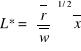
: optymalne zatrudnienie pracy do produkcji
,

-
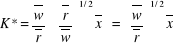
: optymalne zatrudnienie kapitału do

produkcji
,

i kosztu całkowitego dla każdego poziomu produkcji:

-
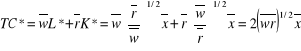
: minimalny koszt

wyprodukowania
.

Jeżeli więc pozwolimy x zmieniać się, to mamy funkcje optymalnej kombinacji czynników:

-

-

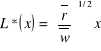
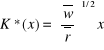
i kosztu całkowitego dla każdego poziomu produkcji:

-
.

Jeżeli teraz pozwolimy w i r zmieniać się, te wyrażenia na L* i K* staną się uogólnionymi funkcjami popytu na czynniki w długim okresie, które zależą od wielkości produkcji. Dlatego nazywamy je funkcjami warunkowymi (conditional).

Uogólniona funkcja kosztu całkowitego w długim okresie wyprowadzona jest więc z uogólnionych funkcji popytu na czynniki:

-
: uogólniona, warunkowa funkcja popytu na pracę w

długim okresie;

-
: uogólniona, warunkowa funkcja popytu na kapitał

w długim okresie;

-
: uogólniona funkcja kosztu całkowitego

w długim okresie.

*****

Porównanie minimalizacji kosztów z minimalizacją wydatków:

Minimalizacja kosztów jest matematycznie identyczna do problemu dualnego konsumenta:

Problem dualny konsumenta: Min M = pxx +pyy p.w.: U = U(x, y)	Minimalizacja kosztów: Min TC = wL + rK p.w.: x = x(K, L)
Popyty skompensowane: uogólnione funkcje popytu:	Warunkowe popyty: K* =K*(w, r, x) L* = L*( w, r, x)
Rozwiązanie: M* (px, py, U) = pxxc^* +pyyc^*	Rozwiązanie: TC*(w, r, x) = wL* + rK*

Koszty przeciętne i krańcowe w LR

Mając uogólnione funkcje kosztów całkowitych w LR możemy wyprowadzić koszty przeciętne i krańcowe w LR:

TC* = LRTC

LRAC = LRTC/x

LRMC = d(LRTC)/dx

Dla: x = K^1/2L^1/2 mamy więc:

LRTC = 2(wr)^1/2x

LRAC = LRMC = 2(wr)^1/2 .

Funkcje kosztów w LR i korzyści skali

Równania: LRTC = 2(wr)^1/2x i LRAC = LRMC = 2(wr)^1/2 ilustrują ważną cechę funkcji kosztów w LR z funkcjami produkcji ze stałymi korzyściami skali (homogeniczność stopnia 1). Jeżeli x = K^1/2L^1/2 , to funkcja kosztów całkowitych w LR jest liniową funkcją produktu, funkcje LRAC i LRMC są równe sobie i stałe niezależnie od wielkości produkcji. Zawsze tak się dzieje, gdy funkcja produkcji charakteryzują stałe korzyści skali.

Zauważ, że LRTC jako funkcja kapitału i pracy jest zawsze homogeniczna stopnia 1. Innymi słowy LRTC i czynniki zawsze rosną w tym samym stosunku:

w(αL) + r(αK) = α(wL + rK).

Z powyższego równania i z: x (ΘK, ΘL) = (ΘK)^α(ΘL)^β = Θ^α+β K^αL^β wiemy, że kiedy zatrudnienie czynników jest zwiększane o ten sam mnożnik, to koszty i produkcja zwiększają się o ten sam (dodatni) mnożnik. Zmiany kosztów są proporcjonalne do zmian produktu:

ΔLRTC = b(Δx), gdzie b to stały czynnik proporcjonalności.

Po przekształceniu:

ΔLRTC

-------- = b.

Δx

Tak więc:

.

Z powyższego równania wynika, że LRTC musi być funkcją liniową. Jej nachylenie, LRMC, jest stałe. Ponieważ koszt wytworzenia 0 jednostek produktu wynosi 0 w LR, to LRTC musi przechodzić przez początek układu współrzędnych:

LRTC = bx i LRMC = LRAC = b. (rys. 11.5)

Rosnące korzyści skali

Z: f(αx, αy) = α^k f (x, y), k > 1 wiemy, że kiedy funkcja produkcji jest homogeniczna, to pomnożenie wszystkich czynników przez α > 1 mnoży produkt przez więcej niż α:

x(αK, αL) = α^kx(K, L) > αx(K, L) dla α, k > 1.

Ale koszty są zawsze proporcjonalne do czynników

(w(αL) + r(αK) = α(wL + rK)). Jeżeli więc czynniki są pomnożone przez dodatnią stałą, to koszty są pomnożone przez tą samą stałą, ale produkcja jest pomnożona przez więcej niż wynosi stała. To oznacza, że produkcja rośnie szybciej niż koszty i:

ΔLRTC

-------- ≈

Δx

muszą maleć. Co więcej, jeżeli funkcja LRMC jest malejąca, to funkcja LRTC musi być wklęsła. I ponieważ zero czynników oznacza zero produktu i zero kosztów, to funkcja LRTC musi być wklęsła od początku układu współrzędnych. Z tego wynika, że funkcja LRAC musi maleć i musi być większa od funkcji LRMC dla każdej wielkości produktu. (rys. 11.6: funkcje kosztów dla funkcji produkcji z rosnącymi korzyściami skali. LRMC maleje implikując wklęsłość LRTC funkcji. Wklęsłość od początku układu implikuje, że LRAC funkcja maleje i jej nachylenie jest większe od nachylenia funkcji LRMC dla każdego poziomu produktu.)

Malejące korzyści skali

Jeżeli funkcję produkcji charakteryzują malejące korzyści skali, to z: f(αx, αy) = α^k f (x, y), 0 < k < 1 wiemy, że

x(αK, αL) = α^kx(K, L) < αx(K, L) dla α > 1 i k <1.

Ponownie koszty są proporcjonalne do czynników

(w(αL) + r(αK) = α(wL + rK)). Jeżeli więc czynniki są pomnożone przez dodatnią stałą, to koszty są pomnożone przez tą samą stałą, ale produkcja jest pomnożona przez mniej niż wynosi stała. To oznacza, że produkcja rośnie wolniej niż koszty i:

ΔLRTC

-------- ≈

Δx

muszą rosnąć. Co więcej, jeżeli funkcja LRMC jest rosnąca od początku, to funkcja LRTC musi być wypukła od początku. Funkcja LRAC musi rosnąć i musi być mniejsza od funkcji LRMC dla każdej wielkości produktu. (rys. 11.7:

funkcje kosztów dla funkcji produkcji z malejącymi korzyściami skali. LRMC rośnie implikując wypukłość LRTC funkcji. Wypukłość od początku układu implikuje, że LRAC funkcja rośnie i jej nachylenie od początku układu współrzędnych jest mniejsze od nachylenia funkcji LRMC dla każdego poziomu produktu.)

Funkcje kosztów przeciętnych o kształcie U i korzyści skali

Przyjęcie funkcji LRAC o kształcie U implikuje założenie, że funkcję produkcji charakteryzują najpierw rosnące, a potem malejące korzyści skali.

Wynika to z faktu, że przy produkcji pewnych dóbr (przy procesie produkcji minimalizującym koszty) dla małej ilości jednostek produktu, koszty jednostkowe (przeciętne) są znacznie wyższe niż koszty wytworzenia większej ilości produktu. (Np. jeśli firma decyduje się produkować tylko niewiele samochodów przy wykorzystaniu linii produkcyjnej, to nie będzie metoda minimalizująca koszty. Pomimo że linia ta pozwala znacznie obniżyć koszty jednostkowe. Linię produkcyjną charakteryzują „economies of scale” korzyści skali oznaczające, że oszczędności na kosztach przeciętnych są możliwe tylko przy wysokich poziomach produkcji.)

Wynikają z tego dwa możliwe kształty dla krzywych LRAC. Z jednej strony LRAC jako funkcja produktu mogą najpierw maleć przy wzroście produkcji, potem być stałe, gdy zakład jest „powielany” i w końcu rosnąć. Z drugiej strony, LRAC krzywa może maleć do punktu minimum i potem rosnąć. Kiedy mówimy o kształcie U, to odnosimy się do drugiego przypadku. Rys. 11.8: funkcja LRTC najpierw jest wklęsła, a potem wypukła odzwierciedlając rosnące korzyści skali, po których następują malejące korzyści skali. LRAC (nachylenie od początku) maleje przy wzroście produkcji, osiąga minimum,
, w punkcie styczności promienia, a potem rośnie.

LRMC jako funkcja produkcji maleje do punktu przegięcia, x_in, i dalej rośnie. LRMC równa się LRAC w
.

Przykład

Wyprowadziliśmy funkcje kosztów w LR dla prostej funkcji produkcji: x = K^1/2L^1/2 . Trudniej jest wyprowadzić funkcje kosztów dla uogólnionej postaci x = AK^αL^β ale jest to korzystniejsze w sytuacjach, kiedy nie znana jest bezpośrednia zależność między L i K, można ją jednak obliczyć na podstawie danych empirycznych. Wykazaliśmy, że obliczenia α i β stanowią bezpośrednie określenie korzyści skali w procesie produkcyjnym. Modelowanie z wykładnikami sumującymi się do 1 implikuje stałe korzyści skali .... .

Wyprowadzenie matematyczne

Aby znaleźć warunkowe popyty na czynniki i funkcje kosztów w LR dla uogólnionej funkcji produkcji typu Cobb-Douglas'a formułujemy problem minimalizacji kosztów firmy przy ograniczeniu produkcyjnym w postaci funkcji Cobb-Douglas'a:

min TC = wL + rK

p.w.: x = AK^αL^β

Lagrangian:

Warunek pierwszego rzędu:

Przekształcając dla λ*:

=

Rozwiązując dla K*:

Wstawiając rozwiązanie dla K* do trzeciego warunku koniecznego:

Rozwiązując dla L*:

: warunkowy popyt na (czynnik) L

Wstawiając L* do
:

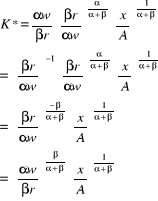
: warunkowy popyt na (czynnik) K

Wstawiając rozwiązanie dla L* i dla K* do funkcji celu:

TC* = wL* + rK* =

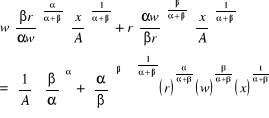
Otrzymane wyrażenie można przedstawić w postaci logarytmicznej:

Powyższe równanie wykorzystywane jest do obliczeń.

Koszty w krótkim okresie (SR) przy jednym zmiennym czynniku

Zał.: K - stały, L- zmienna.

Koszty całkowite w SR

SRTC można wyprowadzić ze ścieżki rozwoju firmy w SR - rys. 11.9:

SRTC są rozkładane na koszty stałe - FC i koszty zmienne - VC:

SRVC = wL

FC = r

SRTC = wL + r

Aby wyprowadzić SRVC skorzystamy z funkcji produktu całkowitego pracy:
. Odwrotność jej:
- rys. 11.10.

Funkcja SRVC jest proporcjonalna do
gdyż SRVC = wL =w
. Rys. 11.11 przedstawia zależność między
i w
. SRVC =0 dla L=0. Aby otrzymać SRTC dodajemy SRVC i FC - rys.11.12.

SRAC i SRMC

SRAVC = SRVC/x = wL(x)/x

AFC = FC/x = r
/x

SRATC = SRTC/x = wL(x)/x + r
/x

SRMVC =

SRMC =

Graficzne i matematyczne wyprowadzenie kosztów w SR

Dla funkcji produkcji
:

Rys.11.13 (komentarz do kształtu i przebiegu)

Dla funkcji: x = K^1/2L^1/2 można wykazać, że MC = min ATC w SR. Minimalizujemy SRATC i pokazujemy, że dla tej wielkości produkcji te koszty są równe:

Rozwiązując dla x:

Wstawiając otrzymany wynik do SRATC:

Wstawiając rozwiązanie dla x do SRMC:

Należy spostrzec, że dla tej funkcji produkcji w minSRATV te dwie funkcje kosztów, SRMC i SRATC, są równe AC i MC w LR. Okazuje się, że ta zależność sprawdza się dla wszystkich funkcji produkcji charakteryzujących się stałymi korzyściami skali.

Skutki malejących przychodów

Przy jednym zmiennym czynniku istnieją trzy ważne cechy funkcji kosztów w SR wynikające z przyjęcia założenia o malejących przychodach z czynnika. Co więcej, ponieważ stałe i malejące korzyści skali również implikują malejące przychody zmiennego czynnika, to te cechy wynikają również ze stałych i malejących korzyści skali:

1. Funkcja SRMC rośnie wraz ze wzrostem produkcji.

Aby wykazać, że ta cecha jest prawdziwa pamiętamy, że SRMC =
. Po przekształceniu:

Jeżeli MP_L maleje i w jest stałe, to funkcja SRMC musi rosnąć.

2. Funkcja SRAVC w końcu musi rosnąc.

Z rys. 10.7 pamiętamy, że jeżeli MP_L maleje, to AP_L w końcu również maleje. Dzieje się tak dlatego, że MP = AP w maksimum AP. Dalej funkcja AP musi maleć. Aby spostrzec, w jaki sposób funkcja AP jest związana z funkcją AVC pamiętamy że SRAVC = SRVC/x = wL(x)/x. Po przekształceniu:

.

Jeżeli funkcja AP_L maleje, to funkcja AVC musi rosnąć.

3. Funkcja SRATC ma kształt U.

Z cechy 1) wynika, że funkcja SRMC w końcu rośnie. Jeżeli SRMC jest rosnąca, to funkcja SRAC jest wypukła i funkcja SRTC leży wyżej niż SRVC o FC - rys.11.14.

Funkcja SRAVC może być wypukła od początku układu współrzędnych bez osiągania minimum. Ale po dodaniu FC do funkcji VC, funkcja SRTC ma punkt przecięcia z osią pionową równy FC. Z tego wynika, że z początku układu można wyprowadzić promień, który będzie styczny do funkcji SRTC i funkcja SRATC będzie miała minimum. Funkcja SRATC ma kształt U.

Koszty w SR przy dwóch (lub więcej) zmiennych czynnikach

Przy dwóch (lub) więcej zmiennych czynnikach analiza się nieco komplikuje i wyniki nie są tak klarowne, jak przy jednym zmiennym czynniku.

Załóżmy, że: w SR kapitał (zakład i maszyny) jest stały, ale zatrudnienie pracy i surowców może się zmieniać. Tym sposobem analiza krótkookresowa upodabnia się do długookresowej.

Oznaczenia:

- stała wielkość kapitału,

m - wielkość zmiennych surowców,

p_m - cena zmiennych surowców.

A więc:

wL + p_mm = SRVC

x = x(L, m;
) - funkcja produkcji

Problem minimalizacji kosztów:

min SRTC = wL + p_mm + r

p.w.: x = x(L, m;
)

Lagrangian:

Pierwsze dwa warunki konieczne:

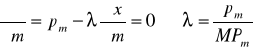
Rozwiązując dla λ:

.

Z powyższego równania wynika, że ten problem jest równoważny wyborowi kombinacji pracy i surowców minimalizującej SRVC przy ograniczeniu produkcyjnym - rys.11.16: linia izokosztów jest SRVC, a izokwanta określona jest przez stały czynnik.

Przy stałym czynniku firma zatrudnia kombinację pracy i surowców minimalizującą SRVC. Ale LRTC nie muszą być zminimalizowane, gdyż firma nie może optymalizować zatrudnienia kapitału. Z ostatniego równania wynika, że firma wybierze taką kombinację pracy i surowców, przy której stosunek produktów krańcowych równa się stosunkowi cen czynników, jak w LR.

Malejące przychody ze wszystkich czynników zmiennych

Jeżeli więcej niż jeden czynnik jest zmienny, to malejące produkty krańcowe poszczególnych czynników już nie są warunkami koniecznymi i wystarczającymi do wzrostu funkcji SRMC i przyjmowania kształtu U przez funkcje SRATC. Zamiast tego funkcje produkcji muszą charakteryzować się malejącymi przychodami ze wszystkich zmiennych czynników przy pewnych czynnikach stałych - rys. 11.17. Jeżeli zatrudnienie pracy i surowców zostaje podwojone, przy stałym zatrudnieniu kapitału, to produkt zwiększa się tylko o 50%. Ponieważ VC podwajają się przy podwojeniu

zatrudnienia zmiennych czynników, to VC rosną szybciej od produkcji i MC rosną. Jeśli MC rosną, to funkcja SRATC ma kształt U (zgodnie z tym, co zostało powiedziane przy rys.11.14).

Zależność między kosztami w LR i SR

Wracamy do firmy zatrudniającej jeden zmienny czynnik do wytworzenia jednego produktu. Na podstawie wcześniej wyprowadzonych równań:

-

-

-

stwierdziliśmy, że dla: x = K^1/2L^1/2 SRMC i SRATC są równe LRMC i LRAC w minimum SRATC. Z tych równań wynikają dwie ważne cechy funkcji kosztów w SR i LR:

1. Funkcje LRTC są obwiedniami funkcji SRTC

Dla danej ilości kapitału (np.
) minimalizowane są koszty pewnej wielkości produkcji w LR. Innymi słowy
= K* dla tej wielkości produkcji. Dla każdej innej wielkości produkcji firma nie może minimalizować kosztów - rys. 11.3. Zawsze, gdy stały kapitał nie równa się K*, firma nie znajduje się w punkcie styczności izokwanty z linią izokosztów. Gdy
≠ K*, to SRTC są większe od LRTC. Gdy
= K*, to te koszt są sobie równe. Tak więc funkcja SRTC jest styczna do LRTC, gdy
= K* i LRTC tworzy obwiednię „od dołu” dla SRTC - rys.11.18.

Lewy wykres pokazuje ścieżki rozwoju w SR i LR. (W LR: x₁ przy TC*₁ i x₂ przy TC*₂.) Jeśli firma zatrudnia
, to może minimalizować koszty wyłącznie dla x₂. Aby produkować x₁ lub x₃ przy
firma zatrudnia L'₁ lub L'₃ jednostek pracy przy SRTC₁ i SRTC₃. SRTC₁ jest większy od TC*₁ i SRTC₃ > TC*₃.

Prawy wykres łączy SR i LR TC jako funkcje wielkości produkcji. W x₂ koszty w SR i LR są sobie równe, ale w x₁ i w x₃ koszty w SR są większe.

(Oznaczmy wielkość produkcji dla
= K* jako
)

Ponieważ funkcja LRTC jest obwiednią funkcji SRTC, to również musi być prawdą, że funkcja LRATC jest obwiednią funkcji SRATC. Kiedy LRTC = SRTC (w
), to LRATC = SRATC, gdyż dzielimy obie TC przez
aby uzyskać AC. W każdym innym punkcie dla równych wielkości produkcji SRATC są większe, gdyż SRTC są większe.

Dodatkowo, ponieważ SRTC i LRTC są styczne w
, to SRMC = LRMC w tym punkcie. Jeżeli x <
, to SRMC < LRMC. Jeżeli x >
, to SRMC > LRMC. (Zanim zilustrujemy to stwierdzenie przejdziemy do 2) cechy.)

2. Jeżeli funkcja produkcji charakteryzuje się stałymi korzyściami skali, to punkt styczności między funkcjami kosztów w SR i LR jest zawsze minimum SRATC. W tym punkcie wszystkie cztery funkcje przeciętne i krańcowe są sobie równe: LRAC = LRMC = SRMC =minSRATC

Stałe linie LRAC i LRMC tworzą obwiednię „od dołu” styczną do każdej SRATC w jej minimum. Wynika to z równań:

-

-

-
.

Rys.11.19 przedstawia cechę 2). Liniowa funkcja LRTC jest linią prostą wychodząca z początku układu współrzędnych i styczną do każdej SRTC w
. Wiemy, że jeżeli promień wychodzący z początku układu współrzędnych jest styczny do funkcji całkowitych, to funkcje przeciętne osiągają minimum lub maksimum i funkcje krańcowe są równe funkcjom przeciętnym w tym punkcie.

Jeśli więc liniowa funkcja LRC jest styczna do funkcji SRTC, to SRAC osiąga minimum i SRAC = SRMC. Co więcej ponieważ ten punkt jest punktem styczności, to SRAC = LRAC i SRMC = LRMC.

Malejące korzyści skali

Jeżeli funkcja produkcji wykazuje rosnące lub malejące korzyści skali, to min SRATC nie jest osiągane w
(w punkcie styczności funkcji kosztów w LR i SR). Dla malejących korzyści skali jest to pokazane na rys.11.20. Ponieważ funkcja LRTC jest ściśle wypukła od początku układu współrzędnych, to nachylenie linii wychodzącej z początku układu współrzędnych zawsze będzie inne niż nachylenie funkcji. Ponieważ funkcja SRTC posiada punkt przecięcia z osią pionową o wartości FC, to osiąga minimum. Ale nigdy nie osiąga go w punkcie styczności funkcji LRTC i SRTC. W punkcie styczności, LRTC = SRTC, LRAC =SRAC i LRMC = SRMC. Ale SRMC nie równa się SRATC i LRMC nie równa się LRATC w tym punkcie. Co więcej, minimum SRATC osiągane jest zawsze w x <
dla każdego zbioru funkcji w SR.

Rosnące korzyści skali

Z odwrotną sytuacją mamy do czynienia przy rosnących korzyściach skali. Minimum SRATC zawsze jest osiągane w x >
dla każdego zbioru funkcji w SR - rys. 11.21. ponownie, linia wychodząca z początku układu współrzędnych określa minimum SRATC i punkt, w którym SRMC = SRATC. Co więcej,
< x czyli wartość określająca minimum SRATC. W punkcie styczności LRTC = SRTC, LRAC =SRAC i LRMC = SRMC. Ale te cztery funkcje przeciętne i krańcowe nie równają się sobie wzajemnie.

Funkcje kosztów w LR w kształcie U

Przy funkcjach LRAC o kształcie U, wszystkie trzy typy zależności między LR i SR można spostrzec - rys.11.22.

W części z rosnącymi korzyściami skali (na lewo od
) minimum SRATC osiągane jest w x >
. Czyli x₁ >
.

W
promień wyprowadzony z początku układu współrzędnych jest styczny zarówno do SRTC, jak i do LRTC. Tak więc wszystkie warunki stałych korzyści skali: LRAC = LRMC = SRMC = SRATC , są spełnione w tym punkcie. Co więcej, wszystkie te funkcje również są równe minimum LRAC i minimum SRATC w tym punkcie. Czyli x₂ =
₂ =
. Na koniec, w części malejących korzyści skali (na prawo od
), minimum SRATC jest osiągane dla x <
. Czyli x₃ jest mniejsze od
₃.

Aby zrozumieć powyższe zależności należy wziąć pod uwagę, co oznacza dla firmy, że ma stałe, rosnące lub malejące korzyści skali. Przy stałych korzyściach skali, minimum ATC jest takie samo niezależnie od rozmiarów firmy zarówno w SR, jak i w LR. Przy rosnących korzyściach skali, przy wielkości produkcji minimalizującej SRATC dla danej ilości stałego czynnika, LRAC zawsze są mniejsze od SRAC. Na rys.11.22 jeśli firma produkuje przy minimum SRATC₁, to może ona zawsze zmniejszyć AC zwiększając zatrudnienie stałego czynnika. Przy malejących korzyściach skali, wielkość produkcji minimalizująca SRATC dla danej ilości stałego czynnika, LRAC również są mniejsze od SRAC. W tym przypadku firma zmniejsza AC zmniejszając zatrudnienie stałego czynnika. Na rys. 11.22 jeśli firma produkuje przy minimum SRATC₃, to może zmniejszyć koszty ograniczając zatrudnienie stałych czynników.

Jeśli LRAC ma kształt U, to firma zmniejsza AC rozwijając się aż osiągnie minimum LRAC w
. W tym punkcie firma minimalizuje AC zarówno w LR, jak i w SR. Co więcej firma nie ma bodźców aby dalej się rozwijać, gdyż zwiększanie zatrudnienia kapitału jedynie zwiększa koszty.

28

---