 | Pobierz cały dokument s.6.wyrownanie.spostrzezen.niejednakowo.doc Rozmiar 596 KB |
Wyrównanie spostrzeżeń niejednakowo dokładnych
Wagi spostrzeżeń
Spostrzeżenia niejednakowo dokładne otrzymamy wtedy, gdy warunki pomiarów są niejednakowe, to znaczy
1) metody pomiarów są różne lub
2) stosujemy różne narzędzia pracy lub
3) obserwatorzy są różni (o niejednakowych umiejętnościach) lub
4) warunki zewnętrzne są niejednakowe.
Dla porównania spostrzeżeń niejednakowo dokładnych wprowadzamy wagi spostrzeżeń.
Wagi obserwacji tej samej wielkości
I definicja wag. Wagi są to liczby dodatnie, które wyrażają ilości jednakowo dokładnych spostrzeżeń i których użycie pozwala wyznaczyć dokładniej mierzone wielkości.
Ta interpretacja wag ma zastosowanie wówczas, gdy wykonamy szereg pomiarów tej samej wielkości przy użyciu tego samego narzędzia, instrumentu, i z pomiarów tych tworzymy średnie arytmetyczne. Jeśli na przykład pomierzono ten sam kąt pierwszego dnia n razy, drugiego n2 razy i trzeciego n3, razy, to waga ![]()
, ![]()
, ![]()
, czyli
![]()
W praktyce wagę traktuje się jako pewien arytmetyczny wyraz zaufania do danego spostrzeżenia.
II definicja wag. Wagi spostrzeżeń są to liczby dodatnie odwrotnie proporcjonalne do kwadratów błędów średnich tych spostrzeżeń:
![]()
(I)
Z tej interpretacji pojęcia wag korzystamy wówczas, gdy przy obserwacjach stosujemy różne narzędzia (instrumenty) i znamy błędy średnie pojedynczych pomiarów wykonanych tymi narzędziami. Często w praktyce stosujemy obie omawiane definicje wag jednocześnie. Ma to miejsce wówczas, gdy przy obserwacjach tej samej wielkości stosujemy instrumenty (narzędzia) o różnej dokładności i różna jest liczba obserwacji każdym instrumentem. Wówczas wagi obserwacji każdym narzędziem będą wprost proporcjonalne do liczby obserwacji oraz jednocześnie odwrotnie proporcjonalne do kwadratów błędów średnich tych narzędzi:
![]()
Wagę spostrzeżenia, względem, którego wyznaczamy wagi innych spostrzeżeń, przyjmujemy równą jedności, a błąd średni takiego spostrzeżenia, zwanego typowym, oznaczamy przez![]()
. Zatem błąd ![]()
jest to błąd średni typowego spostrzeżenia o wadze równej jedności tj. p = 1. Podstawiając we wzorze (I) ![]()
, ![]()
, otrzymamy
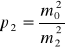
, ogólnie 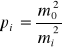
W pewnych wypadkach wygodnie jest wagi wyrażać wprost jako odwrotności kwadratów błędów średnich obserwacji:
![]()
.
Wyrównanie kątów pomierzonych w wieloboku
W pewnym wieloboku o m kątach pomierzono tym samym teodolitem kąty
![]()
,
odpowiednio w liczbie serii
![]()
W oparciu o pierwszą definicję wag przyjmujemy wagi równe
![]()
Przy wyrównaniu kątów powstałą odchyłkę
![]()
(II)
 | Pobierz cały dokument s.6.wyrownanie.spostrzezen.niejednakowo.doc rozmiar 596 KB |