9. JAKOŚĆ UKŁADÓW REGULACJI

Każdy, rzeczywisty UAR pracuje na ogół w trudnych, ciągle zmieniających się warunkach. Zmianie podlega zarówno wartość zadana jak i rodzaj, charakter a także wielkość sygnałów zakłócających. Im mniejsza jest różnica pomiędzy wartością zadaną a wartością rzeczywistą, tym lepsza jakość pracy układu. Jednakże, jak dotychczas nie udało się opracować jednego, uniwersalnego wskaźnika jakości, którego liczbowa wartość pozwalałaby oceniać i porównywać różne układy. Dlatego posługujemy się szeregiem wskaźników pozwalających ocenić wycinkowo najbardziej charakterystyczne fazy pracy badanych układów.

W praktyce inżynierskiej analizy i projektowania UAR ocena jakości sterowania polega na ocenie dwóch stanów układu regulacji:

1. stanu przejściowego,

2. stanu ustalonego.

W pierwszym przypadku mówimy o dokładności dynamicznej, w drugim - o dokładności statycznej.

Dokładność dynamiczna określa zdolność układu do wiernego i szybkiego śledzenia zmian wartości zadanej. Określa się ją stosując wskaźniki bezpośrednie i pośrednie. Omawiane w poprzednim rozdziale pojęcia: zapas modułu i zapas fazy są przykładem wskaźników pośrednich. Dokładność statyczna określa zdolność układu regulacji do utrzymywania wartości regulowanej jak najbliżej wartości zadanej w stanie ustalonym, a więc po zakończeniu procesu przejściowego.

Niżej zostaną omówione podstawowe wskaźniki jakości układów regulacji.

9.1. Dokładność statyczna

Wymagania dotyczące dokładności statycznej układów formułowane są zwykle w postaci podania dopuszczalnych wartości różnicy pomiędzy wartością zadaną a wartością rzeczywistą wielkości regulowanej w stanie ustalonym. Odchylenie to oznaczymy przez ε_ust i nazywać będziemy uchybem ustalonym.

Rozpatrzymy układ automatycznej regulacji złożony z obiektu regulacji, regulatora oraz układu pomiarowego (rys. 9.1). Jeżeli wpływ zakłóceń z i wartości zadanej w_zad można rozpatrywać oddzielnie, co zwykle ma miejsce, to uchyb ustalony w tym układzie będzie sumą dwóch składowych:

(9.1)

gdzie:
- uchyb ustalony wywołany zakłóceniem,

- uchyb ustalony wywołany zmianą wartości zadanej.

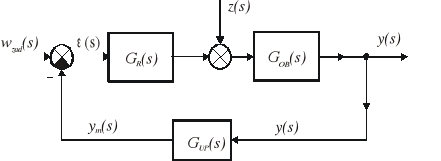
Rys. 9.1. Schemat blokowy układu zamkniętego

W celu ułatwienia analizy statycznej UAR wprowadza się pojęcie transmitancji uchybowej układu. Definiuje się ją jako stosunek transformaty uchybu do transformaty sygnału zakłócającego przy zerowych warunkach początkowych. Uwzględniając wzór (9.1) zdefiniujemy dwie transformaty uchybowe:

Rys. 9.2. Schemat układu pozwalający zdefiniować

Rys. 9.3. Schemat układu pozwalający zdefiniować

Transformaty te wynikają wprost ze schematów przedstawionych na rys. 9.2 i 9.3 uzyskanych z odpowiedniego przekształcenia schematu z rys. 9.1. Definiując G_εz(s) zakładamy, że w_zad jest stałe, natomiast przy określaniu G_εw(s) - że zakłócenia z są zerowe. Dlatego można pominąć odpowiednie sumatory. Jednak znak „minus” sprzężenia zwrotnego należy uwzględnić.

Transmitancje uchybowe dla UAR z rys. 9.1 mają postać:

Korzystając z twierdzenia o wartości końcowej wzory na liczbowe wartości uchybów ustalonych dla omawianego UAR możemy zapisać w postaci:

(9.4)

(9.5)

Jeżeli zakłócenia z wchodzą w innym miejscu do układu, niż to pokazano na rys. 9.1, to zmienia się transmitancja występująca w liczniku wzoru (9.4).

Zależności (9.4) i (9.5) pozwalają ocenić wpływ typu i nastaw regulatora na dokładność statyczną układu. Bardzo interesujące jest zwłaszcza porównanie odchyleń statycznych, które wystąpią w układzie po wprowadzeniu skokowego zakłócenia, w przypadkach, kiedy rolę regulatora będzie pełnił:

1. człon proporcjonalny,

2. człon całkujący.

Schematy blokowe układu odpowiadające tym przypadkom przedstawiono odpowiednio na rys. 9.4a i b. Rysunki powstały na podstawie rys. 9.3. Przyjęto, że obiekt jest elementem inercyjnym o transmitancji
, a układ pomiarowy jest idealny, czyli
.

Rys. 9.4. Schematy blokowe układu: w roli regulatora a) człon proporcjonalny, b) człon całkujący

Zakładając, że we wszystkich przypadkach wprowadzono zakłócenie skokowe o amplitudzie z₀, a więc

na podstawie zależności (9.4) obliczamy:

a)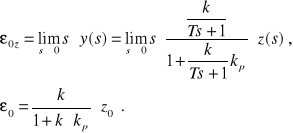
(9.6)

b)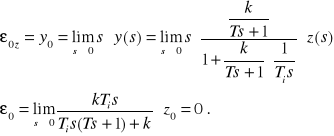
(9.7)

Otrzymane wyniki pozwalają na sformułowanie następujących wniosków:

1. Zwiększenie wzmocnienia proporcjonalnego k_p zmniejsza wartość uchybu ustalonego.

2. Działanie całkujące regulatora sprowadza uchyb ustalony do zera (ε₀ = 0 ).

Wniosek 2 jest czysto teoretyczny. W praktycznych rozwiązaniach istniejące zawsze strefy nieczułości przetwornika pomiarowego i bloku porównującego regulatora oraz niedokładności przetwornika pomiarowego powodują utrzymywanie się pewnego uchybu statycznego, mimo obecności działania całkującego w regulatorze. Stąd często dla zmniejszenia tego uchybu wymaga się, aby przetworniki pomiarowe i bloki porównujące były klasy niedokładności 0,5 a nawet 0,2.

Przedstawione rozważania dotyczące uchybów ustalonych występujących w układach po wprowadzeniu zakłócenia skokowego (lub innego zakłócenia osiągającego określoną, stałą wartość) są wystarczające dla układów regulacji, których zadaniem jest utrzymywanie wielkości regulowanej na stałym poziomie (regulacja stałowartościowa) lub zmieniającym się powolnie według ustalonego programu (regulacja programowa). Natomiast szerszego omówienia wymaga zagadnienie dokładności statycznej serwomechanizmów, których zadaniem jest takie sterowanie wielkością wyjściową y(t), aby nadążała ona za zmieniającym się szybko, często w sposób nieokreślony, sygnałem w_zad(t) (regulacja nadążna). Jako typowe, przyjmuje się wówczas wymuszenia liniowo lub potęgowo narastające, tzn. o stałej prędkości (skok prędkości), o stałym przyśpieszeniu (skok przyśpieszenia), itd.

Dla uogólnienia rozważań podzielimy układy regulacji (sterowania) podobnie jak elementy automatyki, na statyczne i astatyczne.

Pojęcie statycznych i astatycznych UAR związane jest z zachowaniem się wielkości wyjściowej w stanach ustalonych, pod wpływem zakłóceń o stałej wartości (z charakterystyką statyczną układu).

Astatycznym układem regulacji stałowartościowej nazywa się układ, w którym uchyb ustalony równy jest zero. W przeciwnym przypadku układ jest układem statycznym.

W układach statycznych nie ma żadnych elementów całkujących, natomiast w układach astatycznych występuje zawsze co najmniej jeden taki element.

Układ zamknięty jest nazywany układem z astatyzmem l-tego rzędu, jeżeli układ otwarty zawiera l szeregowo połączonych elementów całkujących, tzn. jeżeli jego transmitancję można przedstawić w postaci

(9.10)

przy czym

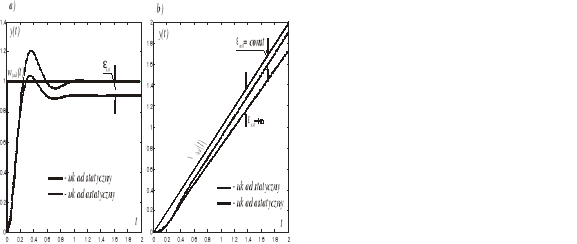
Rys. 9.5. Odpowiedzi na wymuszenie skokowe (a) i liniowo narastające (b) układu statycznego i astatycznego pierwszego rzędu

Do określania wartości uchybów statycznych dogodnie jest skorzystać z rozwinięcia przebiegu
w szereg względem wymuszenia w(t)

(9.9)

gdzie stałe C₀, C₁, ... , C_i, ... nazywane są współczynnikami uchybu i mogą być wyznaczone jako pochodne transmitancji uchybowej
:

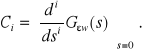
(9.10)

W układach z astatyzmem l-tego rzędu współczynniki C₀, C₁, ... C_l-1 są równe zero, a dopiero współczynnik C_l ma wartość różną od zera;

Można więc powiedzieć, że układ z astatyzmem l-tego rzędu odtwarza bez uchybu statycznego tylko te wymuszenia, których pochodne począwszy od l-tej są dla dostatecznie dużych czasów równe zero. Na przykład, w przypadku wymuszenia liniowo narastającego w(t)=at­­ dla uzyskania
konieczny jest astatyzm drugiego rzędu, w przypadku wymuszenia parabolicznego (skoku przyspieszenia) w(t)=at­² - astatyzm trzeciego rzędu itd. Łatwo zauważyć, że wymagania te są niemożliwe do spełnienia bez wprowadzenia specjalnych członów korekcyjnych przyśpieszających fazę, gdyż już dwa człony całkujące połączone szeregowo wprowadzają przesunięcie fazowe -180° i układ staje się strukturalnie niestabilny.

Należy zaznaczyć, że w przypadku wymuszeń wprowadzanych na wejście obiektu, tzn. z(t) zgodnie z rys. 9.1, do spełnienia podanych wyżej warunków koniecznych dla uzyskania
działanie całkujące musi być zlokalizowane w regulatorze a nie w obiekcie.

Przykład 9.1

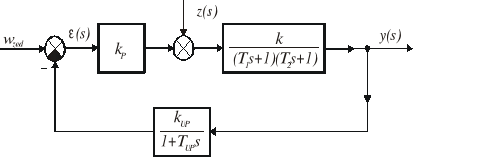
Wyznaczyć wartość uchybu ustalonego ze względu na wymuszenie i zakłócenie w układzie z rys. 4.3 dla następujących danych liczbowych:

T₁ = T₂ = 10 [s], T_UP = 0,5 [s], k = 0,5, k_UP = 1,0, k_P = 7.

Rys. 9.6. Schemat blokowy układu do przykładu 9.1

Rozwiązanie

Transmitancje uchybowe układu mają postać:

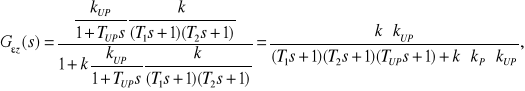
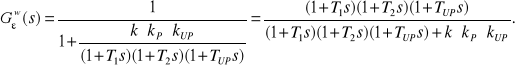
Mając transmitancje uchybowe, możemy policzyć wartości uchybów ustalonych. Przytoczymy szczegółowiej tok postępowania dla obliczenia wartości uchybu ustalonego ze względu na zakłócenie.

Z definicji transmitancji uchybowej mamy:

.

A zatem

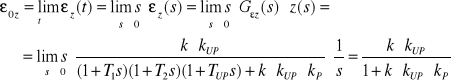
Dla uchybu ustalonego ze względu na wartość zadaną otrzymamy:

9.2. Zwiększenie dokładności statycznej układów regulacji

Dokładność w stanie ustalonym ma istotne znaczenie dla większości układów regulacji. Jest szczególnie ważna w przypadku układów regulacji stałowartościowej (gdy w_zad = const) oraz w układach nadążnych, które mogą np. pracować przy sygnale zadającym zmieniającym się ze stałą prędkością, ze stałym przyspieszeniem lub ogólniej przy stałej k-tej pochodnej sygnału
. Staramy się w układach tych zapewnić pracę ustaloną przy możliwie małych (lub równych zeru) uchybach
i
. Przykładem regulacji stałowartościowej może być stabilizacja temperatury w określonym miejscu urządzenia, w którym są przeprowadzane procesy cieplne. Należy tam, mimo działania różnych zakłóceń, otrzymać wypadkowy uchyb ustalony zawarty w dopuszczalnych granicach. Z kolei jako przykład regulacji nadążnej można podać regulację położenia dwóch elementów nie połączonych mechanicznie ze sobą. Układ regulacji powinien tu zapewnić ruch jednego z tych elementów analogiczny do ruchu drugiego elementu, którego położenie wykorzystuje się do wytworzenia sygnału zadającego. W tym przypadku przy przewidywanym zakresie zmian położenia, prędkości, przyspieszenia itp. elementu drugiego, trzeba przy jego ruchu ustalonym ze stałą prędkością uzyskać możliwie zbliżony ruch elementu pierwszego, również ze stałą prędkością.

Na podstawie rozważań przeprowadzonych w poprzednim punkcie można wysnuć wniosek, że uchyb ustalony doprowadza się do wartości równej zeru przez zastosowanie modyfikacji, po której układ regulacji stanie się astatyczny odpowiedniego rzędu. W tym celu należałoby wprowadzić człony całkujące, których liczbę i miejsce usytuowania dobiera się tak, aby uchyby ustalone
i
stały się równe zeru.

Niestety, ten prosty sposób likwidacji uchybu ustalonego ma zasadniczą wadę, polegającą na niebezpieczeństwie utraty stabilności. Często okazuje się, że układ staje się niestabilny strukturalnie, co oznacza, że nie udaje się uzyskać jego stabilnej pracy ani przez dobór wypadkowego wzmocnienia ani innych parametrów układu, a jedynie przez zmianę jego struktury.

W związku z tym trzeba przyjąć inną strukturę układu, tak żeby wprowadzenie dodatkowych członów nie spowodowało utraty stabilności. Jednym ze sposobów [17] jest włączanie szeregowo w torze głównym dodatkowego elementu o odpowiednio dobranej transmitancji K(s). Element ten tworzy się, korzystając z tzw. członów izodromowych. Na rys. 9.7 przedstawiony jest schemat blokowy prostego pojedynczego członu izodromowego o transmitancji

. (9.11)

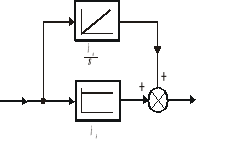
Rys. 9.7. Schemat pojedynczego prostego członu izodromowego

Ogólnie można stwierdzić, że poprawianie dokładności statycznej układu zmniejsza zapas jego stabilności i może spowodować, że układ zamknięty stanie się niestabilny. Dotyczy to zarówno układów statycznych, jak i astatycznych i jest przyczyną konieczności stosowania odpowiedniej korekcji dynamicznej. Przykład 9.2 ilustruje omawiane problemy.

Przykład 9.2

Przeprowadzić analizę stabilności i dokładności statycznej UAR z rys. 9.8 dla sygnału wejściowego w postaci wymuszenia skokowego
i skoku prędkości (
). Sprawdzić wpływ członu izodromowego na własności układu. Dane liczbowe parametrów: k_OB = 1, T₁ = 0,5, T₂ = 0,1. Uchyb ustalony liczyć dla k_P = 0,5k_kr.

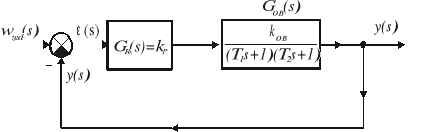
Rys. 9.8. Schemat UAR do przykładu 9.2

Rozwiązanie

Badanie układu przeprowadzimy w kilku etapach.

1. Stabilność układu wyjściowego (rys. 9.8)

Zastosujemy kryterium Hurwitza. Określimy transmitancję zastępczą układu zamkniętego

,

a na jej podstawie równanie charakterystyczne układu

.

Zgodnie z (7.13) warunkiem stabilności badanego układu jest, aby k_P > 0.

Korzystając ze wzorów (9.5) lub (9.9 i 9.10) obliczymy wartość uchybu ustalonego ze względu na wartość zadaną

.

Teoretycznie, zwiększając k_P do nieskończoności możemy zlikwidować uchyb ustalony. Jednak zwiększanie k_P oprócz pozytywnego wpływu na uchyb, ma również niekorzystny wpływ na charakter procesu przejściowego. Na rys. 9.9 przedstawione są procesy przejściowe w układzie z przykładu 9.2 dla kilku wartości k_P ilustrujące zwiększanie oscylacyjności układu.

2. Modyfikacja I

Uchyb ustalony w układzie z rys. 9.8 zgodnie z oczekiwaniami (układ statyczny) jest

różny od zera. W celu jego likwidacji wprowadzimy dodatkowy element w tor główny

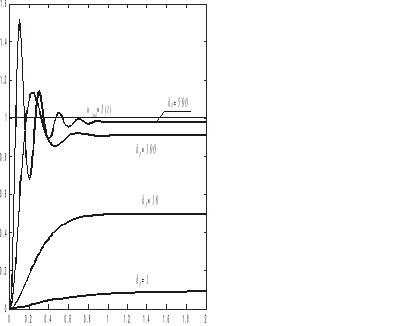
Rys. 9.9. Przykładowe przebiegi procesu przejściowego w układzie z rys. 9.8

układu w postaci idealnego członu całkującego. Sprawdzimy stabilność zmodyfikowanego układu oraz uchyby ustalone dla założonych wymuszeń.

Transmitancja zastępcza układu zamkniętego ma postać

.

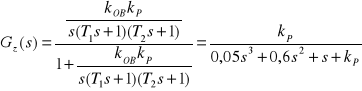
Zakładamy, że k_P > 0. Wówczas pierwszy warunek Hurwitza jest spełniony.

Dla spełnienia drugiego warunku należy obliczyć podwyznaczniki Δ₂ macierzy głównej Γ, która w tym wypadku przyjmuje postać:

.

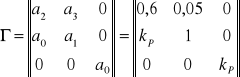
Obliczamy podwyznaczniki Δ₂

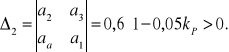
Przyrównując do zera
obliczymy k_kr:

Dla obliczenia uchybów ustalonych skorzystamy ze wzorów (9.9) i (9.10).

Transmitancja uchybowa ma postać

.

Współczynniki:

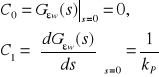
pozwalają wyliczyć uchyb ustalony. W przypadku wymuszenia skokowego
uchyb ustalony
, zaś w przypadku wymuszenia liniowo narastającego
uchyb ustalony
.

Widzimy więc, że człon całkujący daje oczekiwany skutek zerując błąd statyczny spowodowany wymuszeniem skokowym, ale nie eliminuje błędu statycznego spowodowanego liniowo narastającym sygnałem wymuszającym (skokiem prędkości). Dla wyeliminowania tego błędu należałoby wprowadzić drugi człon całkujący w tor główny badanego układu.

3. Modyfikacja 2

Wprowadzamy drugi człon całkujący. Transmitancja zastępcza ma postać

,

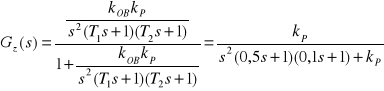
zaś równanie charakterystyczne

pokazuje, że tak zmodyfikowany układ staje się strukturalnie niestabilnym, albowiem brakuje w równaniu członu z s (a₁ = 0). Tak więc, tym sposobem nie daje się zlikwidować uchybu ustalonego w badanym układzie wywołanego skokiem prędkości.

4. Modyfikacja 3

Zamiast drugiego członu idealnie całkującego wprowadzimy człon izodromowy (rys. 9.7). Rozważany układ przyjmie postać jak na rys. 9.10.

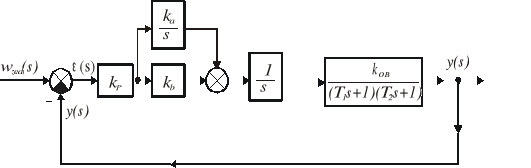
Rys. 9.10. Schemat układu w przykładzie 9.2 po wprowadzeniu członu izodromowego (modyfikacja 3)

Transmitancja zastępcza ma teraz postać:

,

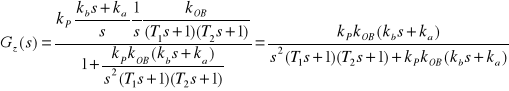
zaś równanie charakterystyczne:

.

Sprawdzamy jak należy dobrać wartości k_a i k_b, żeby przy pozostałych zadanych parametrach układ był stabilny asymptotycznie. Zgodnie z warunkami (7.16) dla układu o równaniu charakterystycznym czwartego rzędu powinny być spełnione następujące nierówności:

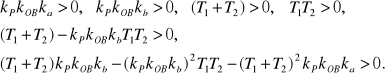
Ponieważ k_P > 0, k_OB > 0, T₁ > 0, T₂ > 0, więc k_a i k_b powinny spełniać następujące warunki

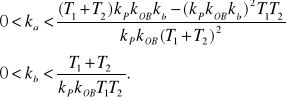
Przy k_P = 5 otrzymamy 0 < k_b < 2,4. Przyjmując k_b = 2 dla k_a otrzymamy nierówność

0 < k_a < 0,55 . . .

Transmitancja uchybowa ma postać:

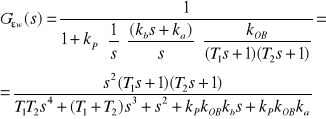
zaś: C₀ = 0 i C₁ = 0, co daje zerowanie wymaganych uchybów regulacji.

Układy astatyczne nie tylko stwarzają problemy ze względu na trudności uzyskania stabilnej pracy, lecz także mają wadę polegającą na tym, że charakteryzują się stosunkowo wolnymi przebiegami przejściowymi. Dlatego, jeżeli nie stawia się wymagania całkowitej likwidacji uchybu ustalonego, często stosuje się regulację statyczną.

9.3. Jakość dynamiczna

Spośród różnych stanów pracy UAR duże znaczenie praktyczne posiada proces przejściowy, wywoływany bądź szybką zmianą wartości zadanej, bądź zmianą wartości sygnału zakłócającego. Z faktu, że układ jest stabilny wynika tylko, że przebiegi przejściowe mają charakter zanikający. Nie wiemy natomiast nic o rodzaju tych przebiegów, o wartości odchyleń maksymalnych, o czasie trwania procesu przejściowego i częstotliwości ewentualnych oscylacji. A wszystkie te pojęcia składają się łącznie na pojęcie jakości dynamicznej układu regulacji.

Jakość dynamiczną określa się za pomocą szeregu wskaźników, odnoszących się do poszczególnych cech przebiegu przejściowego lub charakterystyk częstotliwościowych, bądź za pomocą wskaźników całkowych umożliwiających przybliżoną ocenę całego przebiegu. Omówimy najważniejsze z nich.

Wskaźniki związane z charakterystyką skokową

Przejście z jednego stanu ustalonego do drugiego w UAR może odbyć się co najwyżej na dwa sposoby (rys. 9.11): oscylacyjny (1) lub monotoniczny (2). Niekiedy wyróżnia się przebieg oscylacyjny bez przeregulowania (3), który jednak jest zaliczany do grupy przebiegów monotonicznych.

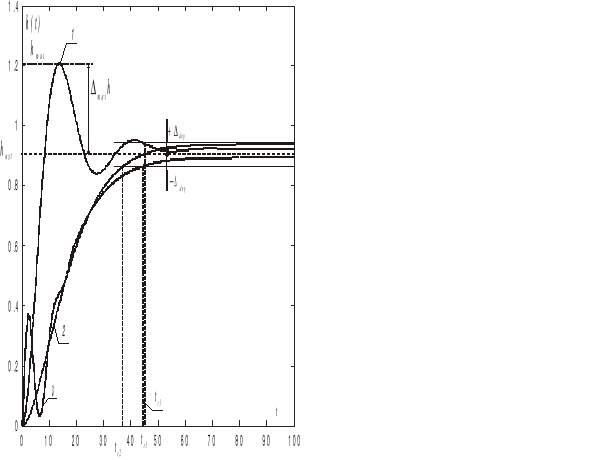
Rys. 9.11. Podstawowe rodzaje przebiegów procesów przejściowych w UAR

Do podstawowych wskaźników jakości procesu przejściowego zalicza się przeregulowanie χ i czas regulacji t_r.

Przeregulowanie χ pozwala ocenić różnicę pomiędzy maksymalną wartością przebiegu przejściowego h_max i ustaloną h_ust. Wyrażane jest w procentach h_ust:

.

Im silniej są tłumione przebiegi oscylacyjne, tym mniejsza jest wartość χ. Przeregulowanie rośnie w miarę zbliżania się do granicy stabilności, aby osiągnąć 100% (oscylacje niegasnące) na tej granicy.

Czas regulacji. Podczas przebiegu przejściowego, następującego po skokowej zmianie zakłócenia (na przykład po skokowej zmianie wartości zadanej), wielkość wyjściowa zmierza do nowej wartości ustalonej (h_ust na rys. 9.11). Czasem regulacji t_r nazywamy czas liczony od chwili przyłożenia wymuszenia do chwili, po której uchyb regulacji jest stale mniejszy od dopuszczalnej wartości
. Zazwyczaj Δ_dop przyjmuje się 5% h_ust .

Niekiedy interpretuje się czas regulacji t_r jako czas trwania przebiegu przejściowego, tzn. przyjmuje się, że układ wytrącony z równowagi przez zakłócenie zewnętrzne osiągnie ponownie stan ustalony po czasie t_r. Interpretacja ta znajduje potwierdzenie doświadczalne, ponieważ stwierdzono, że rzeczywisty czas trwania przebiegu przejściowego jest bliski wartości t_r obliczonej przy założeniu Δ_dop = 5% h_ust. Teoretycznie, przy założeniach upraszczających obowiązujących dla układów liniowych, przebieg przejściowy zanika dopiero dla
, jednak w rzeczywistości - wskutek występowania tarcia, luzów i innych zjawisk nieliniowych - przebieg ten zanika w przybliżeniu po czasie t_r.

Oprócz wymienionych wyżej parametrów z przebiegu przejściowego wyznacza się niekiedy pomocnicze wskaźniki, takie jak:

• maksymalne odchylenie Δ_maxh,

• dopuszczalną liczbę oscylacji - najczęściej 1-2 (niekiedy 3).

Wskaźniki związane z charakterystykami częstotliwościowymi

Zasadniczymi parametrami określanymi na podstawie charakterystyk częstotliwościowych układu są:

• zapas stabilności (modułu i fazy),

• pulsacja odcięcia charakterystyki widmowej części rzeczywistej P(ω) transmitancji układu zamkniętego G(jω),

• maksymalna wartość modułu transmitancji widmowej układu zamkniętego.

Pojęcia modułu i fazy były omówione przy omawianiu zagadnienia stabilności UAR.

Parametry dwóch pozostałych punktów mają ścisły związek z przebiegiem odpowiedzi skokowej układu zamkniętego.

Jeśli, na przykład, charakterystyka P(ω) spełnia warunki

(9.12)

np. jest typu
, to przebiegi regulacji są aperiodyczne.

Jeśli charakterystyka P(ω) jest dodatnia i monotonicznie malejąca, to przeregulowanie χ nie przekracza 18%.

Jeśli P(ω) jest dodatnia, lecz posiada maksimum P_m (tylko jedno), to przeregulowanie χ nie przekracza wartości

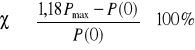
. (9.13)

Jeśli P(ω) ma dodatnie maksimum i ujemne minimum (rys. 9.12), to przeregulowanie χ nie przekracza wartości

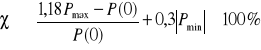
. (9.14)

Czas regulacji jest najczęściej zawarty w przedziale

. (9.15)

Jeśli P(ω) jest niemonotoniczna, to czas t_r jest bliższy górnej granicy określonej wzorem (9.15).

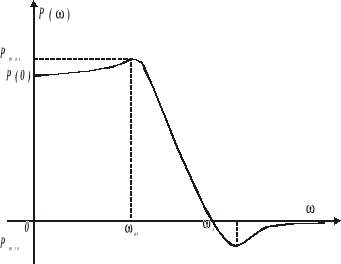
Rys. 9.12. Przykładowy wykres charakterystyki rzeczywistej układu

Pasmo przenoszenia. Jest to zakres częstotliwości, w którym wartości stosunku amplitud wyjścia do wejścia (modułu) oraz przesunięcia fazowego między wyjściem a wejściem (argumentu) utrzymywane są w żądanych granicach.

Pasmo przenoszenia można wyznaczyć dysponując charakterystyką częstotliwościową danego członu automatyki lub zamkniętego układu regulacji. Metodykę postępowania dla dwóch rodzajów charakterystyk: ampltudowo-fazowej i logarytmicznych przedstawia rys. 9.13.

Rys. 9.13. Wyznaczanie pasma przenoszonego 0 < ω < ω_gr, w którym spełnione sa jednocześnie warunki - ϕ₂ < ϕ(ω) < ϕ₁ oraz M₂ < M(ω) < M₁ (lub L₂ < L(ω) < L₁)

W warunkach technicznych dla niektórych członów lub układów (zwłaszcza serwomechanizmów) pasmo przenoszenia jest narzucone. Zadanie może być sformułowane np. w następujący sposób:

Zaprojektować układ (człon) automatyki, który w zakresie częstotliwości do 20 Hz spełniać będzie warunki:

1. M(ω) = (0,7 - 1,4) M_st lub, co równoważne, L(ω) = L_st ± 3 dB;

2. 
   ,

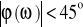
gdzie: M_st - statyczny stosunek amplitud wyjścia do wejścia,

L_st = 20 log M_st.

Zadanie projektanta będzie polegało na takim doborze struktury i parametrów układu, aby charakterystyki częstotliwościowe układu spełniały wymienione warunki.

Maksymalna wartość modułu M_max charakterystyki częstotliwościowej układu zamkniętego, odpowiadająca częstotliwości rezonansowej ω_r, stanowi pewną miarę zapasu stabilności układu. Zwykle wymaga się, aby

lub

,

przy czym L_max = 20 log M_max.

Znajomość charakterystyki częstotliwościowej (minimalno-fazowej) pozwala również wyznaczyć przebieg odpowiedzi y(t) na wymuszenie skokowe. Opierając się na odwrotnym przekształceniu Fouriera otrzymamy zależność analityczną w postaci

, (9.16)

gdzie P(ω) jest składową rzeczywistą charakterystyki częstotliwościowej. Praktyczne obliczanie tej całki polega na aproksymowaniu funkcji P(ω)odcinkami prostymi i wykorzystaniu tablic całek sinusowych. Ogólne wnioski o związkach charakterystyki częstotliwościowej z odpowiedzią skokową wynikające ze wzoru (9.16) można ująć w dwóch punktach:

1. k-krotne zwiększenie skali rzędnych P(ω) powoduje takie samo zwiększenie skali rzędnych y(t),

2. k-krotne zwiększenie skali odciętych ω powoduje k-krotne zmniejszenie skali odciętych t; znaczy to, że odpowiedzi układu są tym szybsze, im szersze jest pasmo częstotliwości przenoszonych przez układ.

Wnioski te zostały zilustrowane przykładami na rys. 9.14.

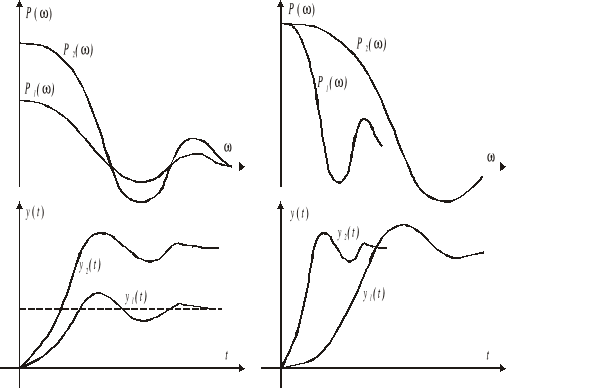
Rys. 9.14. Związki pomiędzy składową rzeczywistą P(ω) charakterystyki częstotliwościowej i odpowiedzią skokową y(t)

9.4. Całkowe wskaźniki jakości

Chęć znalezienia jednego wskaźnika, charakteryzującego w sposób pełny jakość UAR doprowadziła do powstania tzw. całkowych wskaźników. Uwzględniają one założenie, że jakość układu regulacji można ocenić na podstawie wielkości pola regulacji, tzn. pola zawartego pomiędzy krzywą odchylenia regulacji i asymptotą, do której dąży ta krzywa. Im mniejsze jest to pole, tym lepsza jest w sensie ogólnym jakość dynamiczna układu. W sensie ogólnym, gdyż nie wszystkie wskaźniki jakości omówione wcześniej muszą przy tym podejściu być lepsze.

Całkowe wskaźniki jakości są wygodnym narzędziem do porównywania między sobą UAR o podobnej strukturze i doboru parametrów w tych układach. Zazwyczaj stosowane są do oceny wpływu wielkości zadanej na pracę układu, chociaż spotyka się również badanie wpływu zakłócenia przy ich pomocy. Omówimy najczęściej wykorzystywane formy całkowego wskaźnika jakości.

Liniowy całkowy wskaźnik jakości

Stosowany jest do układów, w których spodziewamy się aperiodycznych przebiegów przejściowych i w których
(rys. 9.15a). Obrazuje pole zawarte pomiędzy krzywą uchybu i asymptotą, do której uchyb ten zdąża i wyraża się wzorem

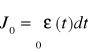
. (9.17)

Minimalizacja tego wskaźnika prowadzi w szczególności do minimalizacji czasu regulacji t_r. Liniowy wskaźnik całkowy niekiedy przedstawiany jest w bardziej ogólnej postaci

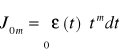
(9.18)

związanej ze współczynnikami błędu:
.

Kwadratowy całkowy wskaźnik jakości

W celu wyeliminowania wpływu znaku uchybu (rys. 9.15b) na wynik, stosuje się kwadratowy całkowy wskaźnik jakości

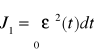
(9.19)

który ma zastosowanie zarówno do przebiegów aperiodycznych jak i periodycznych.

Niech wzór na charakterystykę skokową układu będzie miał postać

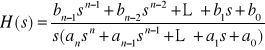
(9.20)

gdzie wielomian
ma wszystkie pierwiastki charakteryzujące się ujemną częścią rzeczywistą, a współczynniki licznika od b_n-1 do b₁ włącznie mogą być równe zeru.

Wówczas kwadratowy całkowy wskaźnik jakości wyraża się wzorem

. (9.21)

gdzie:

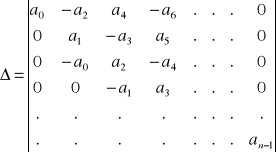
; (9.22)

(i = 0, 1, 2, ..., n-1) - wyznacznik otrzymany z Δ, po zamianie kolumny i + 1 odpowiednio kolumną a_n-1, a_n, 0, 0, ...; w wyznacznikach Δ i
elementy z indeksem mniejszym od zera i większym od n są równe zeru;

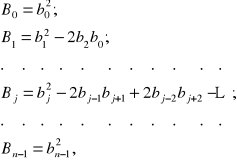
(9.23)

gdzie we współczynnikach B_j elementy z indeksami mniejszymi od 1 i większymi od n są równe zeru.

W niektórych podręcznikach z zakresu automatyki przytoczone są gotowe wzory na J₁. Np. w [13] J₁ obliczone jest dla n = 2; 3; 4; 5 i 6.

Dla uniknięcia wpływu znaku uchybu regulacji na wynik badania niekiedy stosuje się wskaźnik całkowy

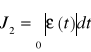
. (9.24)

Jednak większe problemy (zwłaszcza przy obliczeniach komputerowych) z określeniem bezwzględnej wartości w porównaniu z operacją podnoszenia do kwadratu i niektóre inne niedogodności powodują, że ten wskaźnik jest wykorzystywany rzadziej.

Modyfikowane całkowe wskaźniki jakości

Poszukiwania jednego, najlepszego wskaźnika jakości spowodowało, że stosuje się niekiedy zmodyfikowane postacie całkowych wskaźników jakości . Dwie z nich, to:

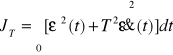
(9.25)

gdzie: T - stały parametr. Czym mniejsza wartość wskaźnika J_T, tym mniejsza odchyłka wielkości wyjściowej od krzywej wykładniczej ze stałą czasową T, zwaną ekstremalą

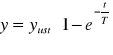
oraz

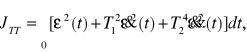
(2.26)

która minimalizuje odchyłkę wielkości wyjściowej od ekstremali opisanej równaniem

gdzie
i
.

Przykład 9.3

Dany jest układ regulacji jak na rys. 9.15. Przy ustalonej stałej czasowej T dobrać wzmocnienie k > 0, aby osiągnąć minimum całki z kwadratu błędu.

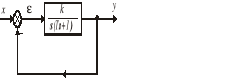
Rys. 9.15. Schemat układu regulacji do przykładu 9.3

Rozwiązanie

Transmitancja układu przedstawionego na rysunku ma postać:

(9.27)

Równanie różniczkowe tego układu :

(9.28)

Współczynniki a_i i b_i tego równania różniczkowego określimy z zależności:

.

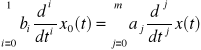
Lewa strona równania (9.28) ma jeden współczynnik

a wartości współczynników prawej strony:

.

Z równania (9.23) wynika, że współczynnik

.

Aby obliczyć ze wzoru (9.21) kwadratowy, całkowy wskaźnik jakości musimy obliczyć tylko wyznaczniki
i
ponieważ współczynniki B_i oraz b_i dla
są równe zeru.

Wyznacznik
:

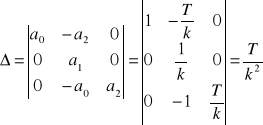
(9.29)

Wyznacznik
otrzymamy z wyznacznika
zamieniając kolumnę (i+1) kolumną:

Wyznacznik
będzie miał postać:

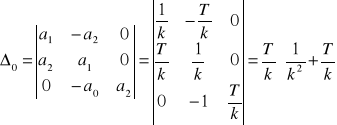
(9.30)

Wstawiając te wyrażenia do równania (9.21) otrzymamy:

(9.31)

Minimalną wartość J₁ otrzymamy wybierając największą z możliwych w układzie wartość k.

Michał Chłędowski WYKŁADY Z AUTOMATYKI dla mechaników 188

189 9. Jakość układów sterowania

---