Nr ćwiczenia: 204	Data: 04-06-2001r.	Marek Frątczak		Wydział Elektryczny	Semestr II	Grupa: E-9
Prowadzący: mgr Jarosław Gutek			Przygotował: Marek Frątczak	Wykonał: Marek Frątczak	Opracował: Marek Frątczak	Ocena:

Temat : Cechowanie termoogniwa.

1. Wstęp teoretyczny.

Termoogniwo stanowią dwa różne przewodniki połączone ze sobą w sposób przedstawiony na rysunku. Jeżeli punkty łączenia znajdują się w różnych temperaturach, Wówczas powstaje między nimi różnica potencjałów, zwana siłą termoelektryczną. Jej wielkość zależy od rodzaju przewodników tworzących termoogniwo oraz od różnicy temperatur i wyraża się wzorem

Współczynniki
charakteryzują zastosowane materiały. Przedstawiony efekt nazywamy zjawiskiem Seebecka.

Bezpośrednią przyczyną wystąpienia siły termoelektrycznej jest różna wartość napięć kontaktowych w złączach posiadających różne temperatury. Istnienie napięć kontaktowych związane jest ze zjawiskami elektronowymi w metalach. W każdej temperaturze istnieje pewna ilość elektronów, które posiadają energię kinetyczną wystarczającą do wykonania pracy wyjścia W, a zatem do wyjścia na powierzchnię metalu. Te elektrony tworzą tzw. prąd termoemisji skierowany prostopadle do powierzchni metalu. Gęstość prądu termoemisji określona jest prawem Richardsona - Dushmana i dla obu przewodników z rys. 1 wynosi odpowiednio

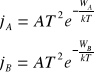
Gdy oba przewodniki zbliżymy na bardzo małą odległość, elektrony opuszczające metal A będą przechodziły do metalu B i odwrotnie. W sytuacji przedstawionej na rys. 1
ze względu na wartości prac wyjścia
. Przewaga prądu
prowadzi do zwiększenia ilości elektronów w metalu B i do powstania ich niedomiaru w metalu A. W tej sytuacji metale naładują się przeciwnymi znakami i powstanie między nimi różnica potencjałów o takim kierunku, że dalszy przepływ elektronów od A do B zostanie utrudniony i w końcu zrównoważony przepływem od B do A. W stanie równowagi strumienie elektronów w obu kierunkach są takie same, co oznacza:

Powyższe równanie odzwierciedla fakt, że elektrony opuszczające metal A muszą wykonać, oprócz pracy wyjścia, pracę przeciwko różnicy potencjałów
. Tę różnicę potencjałów, powstającą w wyniku zetknięcia się dwóch przewodników, nazywamy napięciem kontaktowym. Jego wartość określona jest tylko przez różnicę prac wyjścia obu metali

Siła termoelektryczna może wystąpić także w przewodniku jednorodnym ( bez złącz), gdy między jego końcami wytworzymy różnicę temperatur. To zjawisko nosi nazwę efektu Thomsona i jest prostą konsekwencją zależności energii Fermiego od temperatury.

.

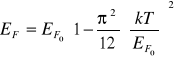
Zjawisko Peltiera - pobieranie lub wydzielanie ciepła przy przepływie prądu przez złącza metali.

Wzorcowanie termoogniwa.

W celu znalezienia napięć termoelektrycznych odpowiadających określonym różnicom temperatur
stosujemy układ przedstawiony na rysunku 2. Jedno złącze znajduje się w naczyniu zawierającym mieszaninę wody z lodem (
), zaś drugie w naczyniu z wodą, której temperaturę zmieniamy za pomocą grzejnika G. Temperaturę T mierzymy czujnikiem oporowym
, a jej wartość odczytujemy za pomocą miernika cyfrowego. Stosuje się trzy różne termopary:
. Przełącznikiem Pr w obwód każdej termopary można włączyć miliwoltomierz cyfrowy (mV).

2. Dane eksperymentalne.

Temperatura rosnąca[^0C]	Napięcie termoelektryczne U[mV]						Temperatura malejąca [^0C]
		A	B	C	A	B		C
30	1,14	1,08	0,74	1,20	0,94	0,81	30
35	1,16	1,28	0,92	1,24	1,11	0,93	35
40	1,16	1,35	1,09	1,28	1,41	1,15	40
45	1,17	1,42	1,35	1,30	1,73	1,33	45
50	1,18	1,70	1,40	1,31	1,76	1,53	50
55	1,19	1,76	1,53	1,32	1,91	1,77	55
60	1,19	2,04	1,62	1,34	2,07	1,91	60
65	1,20	2,22	1,77	1,34	2,25	2,04	65
70	1,21	2,57	1,99	1,33	2,40	2,22	70
75	1,23	2,71	2,11	1,37	2,64	2,41	75
80	1,25	2,92	2,31	1,39	2,82	2,64	80
85	1,25	3,08	2,44	1,39	3,17	2,74	85
90	1,28	3,31	2,60	1,39	3,29	2,81	90
95	1,30	3,48	2,65	1,38	3,48	2,87	95
100	1,31	3,65	2,98	1,41	3,65	2,98	100

ΔT=0,1[⁰C]

ΔU=0,01[mV]

3. Obliczanie regresji liniowej.

Do obliczeń regresji liniowej dla poszczególnych termopar oznaczenia:

A - stała wartość

B - współczynnik regresji

R - współczynnik korelacji

Do obliczeń wykorzystałem program do skryptu St. Szuby.

• Podczas grzania:

Termopara A

A=1,064 ΔA=0,00977

B=0,00232 Δ B=0,00014

r=0,9763

Termopara B

A= - 0,1895 ΔA=0,06932

B=0,03837 ΔB=0,00101

r=0,9955

Termopara C

A= - 0,1273 ΔA=0,04639

B=0,03016 ΔB=0,00068

r=0,9967

• Podczas stygnięcia:

Termopara A

A=1,194 ΔA=0,02795

B=0,00204 ΔB=0,00041

r=0,8105

Termopara B

A= - 0,1669 ΔA=0,06215

B= 0,03809 ΔB=0,00091

r=0,9963

Termopara C

A= - 0,07282 ΔA=0,07260

B= 0,03214 ΔB=0,00106

r=0,9930

Z wykonanych obliczeń regresji wynika, że wartości współczynników termoelektrycznych dla poszczególnych termopar wynoszą:

Dla grzania:

A - α₁=(2,321±0,1426)⋅10^-3

B - α₁=(38,37±1,012)⋅10^-3

C - α₁=(30,16±0,6773)⋅10^-3

Dla stygnięcia:

A - α₁=(2,036±0,4080)⋅10^-3

B - α₁=(38,09±0,9074)⋅10^-3

C - α₁=(32,14±01,060)⋅10^-3

4. Wnioski.

Konieczność dokonania pomiaru siły termoelektrycznej dla trzech termopar powodowała, iż nie zawsze wszystkie trzy pomiary były dokładnie zmierzone ze względu na bardzo szybkie ogrzewanie i chłodzenie się urządzenia. Powodowało to powstawanie błędu pomiaru, który przewyższał błąd wynikający z dokładności narzędzi pomiarowych. Szczególnie było widoczne to podczas stygnięcia. Z porównania współczynników termoelektrycznych dla grzania i stygnięcia wynika, że są one zbliżone, jednak w przypadku stygnięcia obarczone są większym błędem. Pomiary dla termopary A mogą być błędne, ponieważ urządzenie pomiarowe pokazywało cały czas prawie identyczną wartość.

1

4

---